メールマガジン宝箱 Mail magazine

　組分けテストで偏差値アップを実現するポイントは、テスト前半の小問集合で失点を最小限にとどめることです！速さのグラフの見方、平面図形での補助線の引き方、そして分数、小数を含めた数に関する問題などの基本問題で、わかったつもりのままの曖昧な理解をなくすことを目標に、徹底的に復習を進める。それが偏差値をアップさせるかどうかの分かれ目になります。基本問題をいかに確実に得点するかを中心に説明していきます。ぜひ偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせれば、偏差値を別次元のランクにまで上げることができます！頑張ってください！
予想問題はこちらのページで無料公開します！

【第5位　点の移動：点は必ずしも辺の上を動くとは限りません！】

　点の移動では、三角形や四角形の辺の上を点が動く問題を、これまで多く解いてきましたが、問題の難度が上がると、点は辺の上を動くとは限らなくなります。例えば次のような対角線上を点が動く問題に対応できているかどうかチェックしてみてください。

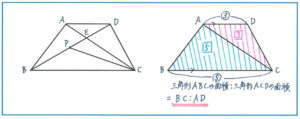
　一見複雑そうな問題ですが、面積比の基本的な考え方を使えば、決して難しくはありません。
　最初のポイントは、三角形ＡＢＣと三角形ＡＣＤの面積比がすぐに答えられるかどうかです。ＡＤとＢＣが平行ですので、三角形ＡＢＣと三角形ＡＣＤは高さが同じと考えられます。そこで、面積比はそれぞれの三角形の底辺の長さの比と等しくなります。台形を使った面積比の問題では、このパターンが頻出ですので、しっかりおさえておきましょう。三角形ＡＢＣの面積：三角形ＡＣＤの面積＝ＢＣ：ＡＤ＝5：3となります。ここで三角形ＡＢＣの面積が64÷(3＋5)×5＝40（平方cm）と求められます。
　同じように、三角形ＡＢＥと三角形ＣＢＥはＡＥ、ＣＥを底辺とすれば高さが同じですので、三角形ＡＢＥの面積：三角形ＣＢＥの面積＝ＡＥ：ＣＥ＝1：3となり、三角形ＣＢＥの面積が、40÷(1＋3)×3＝30（平方cm）となります。
　最後はこれまでの作業と逆の進め方ですが、基本的な考え方は同じです。三角形ＣＥＰの面積：三角形ＣＢＰの面積＝ＥＰ：ＢＰで、三角形ＣＥＰの面積が10平方cmであることから、ＥＰ：ＢＰ＝10：(30－10)＝10：20＝1：2と、答えに行き着くことができます。
　このように、点の移動の問題では、面積比の基本を活用するケースがとても多くあります。この後にも面積比についての説明がありますが、面積比の基本が曖昧な場合には、デイリーを戻って復習をしてください。

【第4位　面積比：問題を解くために有効な補助線を引けていますか？】

　平面図形の問題の中で次のような問題に対応するためには、有効な補助線が必要です。

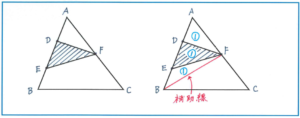
　ポイントは面積比をいかにして辺の比に置き換えるかです。ここでも第5位の問題と同じく、「高さが同じ三角形の面積比は底辺比と等しい」ことを利用します。その目的で補助線を引くのです。
　この問題では、点Ｃと点Ｅ、または点Ｂと点Ｆを結ぶ補助線を引く方法があります。どちらでも構いませんが、予想問題では点Ｃと点Ｅを結ぶかたちで進めていますので、こちらでは点Ｂと点Ｆを結ぶこととします。
　右の図のように補助線が入ることで、面積比を底辺比で表せる図形がハッキリと見えてきました。三角形ＢＥＦと三角形ＤＥＦ、三角形ＡＤＦはすべて高さが同じですので、その面積比はＢＥ：ＤＥ：ＡＥ＝1：1：1となります。そこで斜線の入った三角形ＤＥＦの面積をマル1としましょう。すると三角形ＢＥＦ、三角形ＡＤＦともにマル1なので、三角形ＡＢＦの面積はマル3となります。
　そこで視点を切り替えます。三角形ＡＢＦと高さを同じにする三角形はないか…すぐとなりに三角形ＢＣＦがありますね。この2つの三角形の面積比は底辺比のＡＦ：ＣＦ＝1：1となり、三角形ＢＣＦの面積もマル3として表すことができます。よって、三角形ＡＢＣの面積はマル3＋マル3＝マル6となり、マル1が20平方cmなので、マル6は20×6＝120より、三角形ＡＢＣの面積が120平方cmと求められます。
ポイントはあくまで面積比を辺の長さの比から求めることですが、1本の補助線を引くだけで、その解法を使いこなすことができます。補助線の引き方に注意して復習を進めましょう。

【第3位　相似：比を使えば、複雑な計算を回避することができます！】

　平面図形で円やおうぎ形の問題では、比が使えないかどうか、まず確かめてみましょう。3.14計算をできるだけ少なくすることが、問題を解くスピードアップ、正確さのアップにつながります。そのためには比の活用がとても有効なのです。
例えば次のような問題。

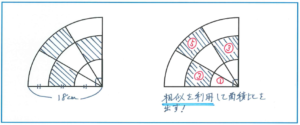
　一見すると、斜線部分を動かしてシンプルなおうぎ形に変形する等積移動の問題のようですが、実はうまくシンプルな図形には変形できないのです（パズルで言うピースの数が合わないです）。それではどうするか…ここでまた比が登場します。まず前提として、中心角30度のおうぎ形どうしは相似になることをとらえておきましょう。相似というと三角形や四角形などで見られることが多いですが、円やおうぎ形でも相似の関係は成り立ちます。その理解が曖昧にならないように注意してください。
　右の図で表したように、最も小さなおうぎ形の面積をマル1とすると、2番目の大きさのおうぎ形の面積がマル4となるため、その間の部分はマル4－マル1＝マル3、同様にして、最も外側の図形はマル9－マル4＝マル5と表すことができます。斜線部分の合計はマル3×2＋マル5＝マル11となります。
マル1の面積は6×6×3.14×30/360＝9.42（平方cm）なので、求める面積は、9.42×11＝103.62（平方cm）です。
　最後の小数計算こそ少し手間取りますが、個々の部分の面積を求めるよりは断然計算が楽ですし、間違える可能性も激減します。円やおうぎ形でも相似を使えることをどうか確認しておいてください。

【第2位　速さとグラフ：速さを範囲で答えさせる問題に対応できていますか？】

　単元を問わず、小学生のお子様方は答えに範囲や幅がある問題を苦手とすることが多いです。例えば「何個以上、何個未満で答えなさい」や「あてはまる分数をすべて答えなさい」といったタイプの問題です。答えがひとつに定まらない気持ちの悪さが苦手意識に結びついてしまっているのでしょう。
速さの問題でも答えに幅（範囲）があるかたちで答えさせるものがあります。例えば次のような問題。

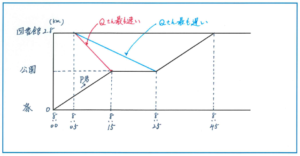
　速さのグラフの基本として、グラフの傾きが急なほど速度は速く、傾きがなだらかなほど遅いことはまずおさえておきましょう。それが右上がりのグラフであればすぐにわかるけれど、右下がりのグラフになると一気にわかりづらくなることはないでしょうか。グラフが上向きか下向きかに関わらず、速いか遅いかの判断はグラフの傾きでできることを確認しましょう。
　あとはＰ君の動きを表したグラフに、Ｑさんの動きをかき入れてみれば、一気に解決に向えます。
　上の図の赤線でかいたグラフはＱさんが最も早い時間にＰ君に会える状況、つまりＱさんの速度が最も速い状況です。一方、青線でかいたグラフはＱさんが最も遅い時間にＰ君に会える状況、つまりＱさんの速度が最も遅い状況です。ここではわかりやすいように色を使っていますが、テストでは色ペンはもちろん使えませんので、太線と点線などで使い分けてください。
あとはグラフで示された情報を確実に使いこなせば、式を立てることは難しくありません。
8時45分－8時25分＝20分
・・・Ｐ君が公園から図書館までにかかった時間
80(ｍ/分)×20分＝1600ｍ
・・・公園から図書館までの距離
1600ｍ÷(15－5)分＝160(ｍ/分)
・・・Ｑさんの最も速い速度
1600ｍ÷(25－5)分＝80(ｍ/分)
・・・Ｑさんの最も遅い速度
よって答えは、毎分80ｍ以上160ｍ以下と求められます。
　答えに幅があっても問題内容やグラフの内容をしっかり読んで、答えを求めるために必要な情報を的確にキャッチすれば、決して恐れることはありません。そのためには、問題文の大事な箇所に線を引くなどの方法も有効です。

【第1位　数の問題：四捨五入の解き方が曖昧になっていませんか？】

　5年生最後の組分けテストの攻略ポイントの第1位が四捨五入と聞くと、意外に思われるかもしれません。ところが、この四捨五入のような数の問題で苦戦しているお子様が多くいらっしゃるのです。
　例えば次のような問題でスムーズに正解に行き着けていますでしょうか。

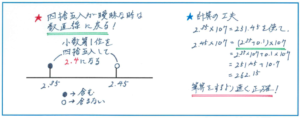
　まずは小数第1位まで求めて2.4になる数の範囲が、2.35以上2.45未満になることが即答できているか、しっかりチェックしてください。正解するだけでなく、即答できることがポイントです。少しでも曖昧な場合は、左の図のような数直線に戻って理解を確かめてください。
　次に、2.35×107＝251.45、2.45×107＝262.15の小数計算をミスなく進められるかどうか。2.45×107で、2.35×107に0.1×107＝10.7を足すという計算の工夫ができればなおよいでしょう。
　そして最後に、251.45から262.15の範囲に入る整数が、252から262となるため、その個数は262－252＋1＝11（個）と、最後に1を足すことを忘れずにできているかどうかも確認してください。
　このタイプの問題は、テスト序盤の小問集合で出される可能性が高いです。組分けテストで偏差値をアップさせるには、計算問題、小問集合での失点をいかに少なくするかがポイントになります。ここで取り上げた四捨五入など数の問題を含む基本問題で少しでも苦手に感じているところがあれば、それを優先してつぶすように復習を進めてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。