メールマガジン宝箱 Mail magazine

　今回のマンスリーでの偏差値アップのポイントは、問題内容に合わせた正確な式を立てることです。ニュートン算や場合の数、平面図形など、今回のテスト範囲は多岐に渡ります。それぞれの単元について基本理解を徹底したうえで、考え方の方針を確立してから、正確に式を立てるという流れが求められます。特にニュートン算や速さのつるかめ算は、式の立て方が理解できなければ太刀打ちできない問題ですが、問題の出され方はパターン化されていますので、解法のプロセスさえしっかり固まれば攻略の糸口がつかめます。自分がかいた式の意味をもう一度確認して、式で出した答えをそのまま問題の答えにしてよいのか、徹底チェックを重ねることが、得点力の大幅アップに直結します！
　ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせれば、偏差値のレベルを飛躍的にアップさせることができます！頑張ってください！
予想問題はこちらのページで無料公開します！

【第５位　速さ：つるかめ算を使った速さの応用問題に対応できていますか？】

　速さが途中で変わるタイプ問題で、次のように変わる前と後の速さ、道のりの合計、時間の合計が分かっている問題では、つるかめ算の考え方を使うことは、問題を見た瞬間に対応できるようにしておきたいところです。例えば次のような問題です。

　つるかめ算の考え方を使うことがわかれば、あとは「1本100円のボールペンと1本80円の鉛筆を合わせて20本買った時の合計代金が1760円でした。ボールペンは何本買いました」といった基本的な解き方は変わりません。注意するのは最後に何を求めるかです。今回のように道のりを求める場合には、式から得られた時間に速さをかけて求めますが、そこで使う速さを間違えないように注意しましょう。
　まず内容を整理すると、太郎君が歩いた時間の合計は、9時30分－7時－10分＝2時間20分なので、上の左のようにまとめることができます。ここから式を立てます。なお、帯分数はa・c/bのかたちで表します。
　求める道のりはＰ地点からＲ地点までの道のりなので、太郎君が時速6㎞で歩いた時間を求めればよいことになります。上の右の図の面積図の斜線部の面積は、12－4×2・1/3＝8/3（㎞）にあたりますから、8/3÷(6－4)＝4/3（時間）が時速6㎞で歩いた時間なので、答えは6×4/3＝8（㎞）と求められます。
　つるかめ算は式の立て方は難しくありませんが、要素を間違って選ぶ（この問題であれば、6×2・1/3－12という式を立ててしまう）ことがないように十分に注意しましょう。

【第４位　ニュートン算：線分図にできるだけ情報をかき込んで内容を整理しましょう！】

　ニュートン算は問題文が複雑なため、やりづらさを感じてしまいがちですが、線分図で内容を整理できれば、そこからの進め方は決して難しくはありません。線分図をかく練習をできるだけ重ねて、いかに慣れるかがポイントです。線分図をかく際には、問題で与えられた情報をできるだけかき入れて、問題内容を視覚的にも把握できるようにしましょう。
　例えば次のような問題。

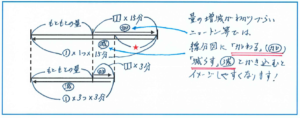
　排水口1つが1分間にくみ出す水の量をマル1（メルマガでは○の中に数字をこのように表します）、1分間に入れられる水の量をシカク1とします。ニュートン算の難しいところは、加わる量と減る量が同時に発生している点です。そこで、もともと水そうにあった量を「もともとの量」として、加わる量を一旦「もともとの量」に加えた後に、排水口からすべての量を流す、と考えます。線分図に「加わる」「減らす」（上の図のように加、減でもよいでしょう）とかき込んでおくと、その流れがよりわかりやすくなります。
　ここからは、マル1とシカク1のどちらかに統一することで、一気に正解に進んで行きます。
　線分図の★の部分に注目して、★をマルとシカク両方で表すことで下の式が表せます。
　★＝シカク15－シカク3＝マル15－マル9より、
　シカク12＝マル6
　シカク2＝マル1
となります。
線分図の上の方で、もともとの量をシカクで表すと、
マル15－シカク15＝シカク30－シカク15＝シカク15
排水口2つで1分間に流す量はマル2＝シカク4
入れられる水の量はシカク1
なので、シカク15÷(シカク4－シカク1)＝5
より5分と求められます。
ニュートン算は上記のようなマルやシカクを使った式を立てられるかどうかがポイントです。そのためにも問題の内容を正確にとらえるために、「加わる」「減らす」といった言葉を含めて、できる限りの情報をかき込むようにしましょう。

【第３位　数の性質：Ｎ進法の問題に対応できていますか？】

　数の性質の中でもＮ進法の問題は苦手にしている生徒さんが多い単元です。普段使っている10進法との違いがわかりづらく、なかなか式が立てられないことで苦手意識を持ってしまっていると考えられます。例えば次のような問題に対応できているでしょうか。

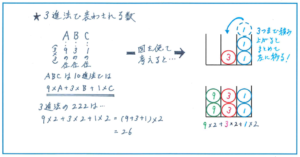
　一見してＮ進法の問題とは見えない複雑そうな問題ですが、3以上の数を0、1、2の位を上げることで表すということから、この問題は3進法で表された222を10進法に直す問題であることにまず気づく必要があります。
　あとは上記のように、各位の下にそれぞれが何の位なのかを記入すれば、一気に解きやすくなります。Ｎ進法の問題は頭の中だけで解き進めようとすると、複雑さを極めてしまいます。求める数字の位が何の位なのかをかき出すことで、解法のきっかけを手にしましょう。
　この問題では、1の位、3の位、9（3×3）の位にそれぞれ2がありますので、9×2＋3×2＋1×2＝(9＋3＋1)×2＝13×2＝26より、26が正解となります。
　Ｎ進法が苦手なお子様は、まずは今回の3進法のような、Ｎの値が小さなケースで練習を重ねて慣れを身につけるとよいでしょう。

【第２位　場合の数：2つの和が一定の組合せを計算で求められていますか？】

　場合の数の中で、ただあてはまるケースをかき出すのではなく、途中から計算を使って解き進められるタイプの問題があります。例えば次のような問題。

　この問題のように、単価と合計がわかっている問題では、表を使ってかき出す方法があります。確かにもれなく選び出せるメリットはありますが、より時間を短縮できる解法があります。
　まず、リンゴをＡ個、梨をＢ個買うとすると、以下のような式になります。
　120×Ａ＋100×Ｂ＝2000
　ゼロが多くなりますので、両辺を10で割って少しでも数をスッキリさせましょう。
　12×Ａ＋10×Ｂ＝200
　さらに両辺を2で割って、
　6×Ａ＋5×Ｂ＝100
　で考えていきましょう。
　ここで、この式を満たすＡとＢの組み合わせを調べるのですが、（Ａの個数、Ｂの個数）で表すとして、まず（0、20）が式を満たします。問題ではどちらも1個以上買う、という条件がありますので、答えには含まれませんが、解法のスタートとして、この組み合わせを使います。
ここから合計の200を変えずにＡとＢの組み合わせを変えていくには、Ａの値が増えることによって6×Ａが増える量と、Ｂの値が減ることによって5×Ｂが減る量が等しくなればよいのです。つまり、Ａを5ずつ増やしてＢを6ずつ減らせば、合計は変わらなくなります。
　そこであてはまる組合せは（0、20）（5、14）（10、8）（15、2）となり、このうち（0、20）は条件に合わないことから、答えが3通りと求められます。
　表にまとめて数を探すよりも、ルールをもって探す方がより速く正確に解くことができます。

【第１位　平面図形：同じ長さを2種の比で表した問題に対応できていますか？】

　平面図形で相似や面積比を用いて長さの比を求める問題がありますが、何本かの線が入り交じる次のような問題にはどのように対応すればよいでしょうか。

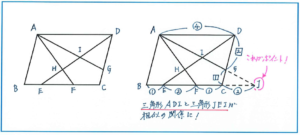
　ＤＩ：ＩＨ：ＩＥという3つの長さの比を一気に求めようとしても、なかなか糸口がつかめません。このようなタイプの問題では、全体を含める線分について異なる2つの比で表し、最後に値を調整する方針で進めると正解に行き着けます。
　具体的には、ＤＨ：ＨＥの比、ＤＩ：ＩＥの比をそれぞれ求めるのですが、そこで必要となるのが相似の関係の活用です。平行四辺形を様々な角度から見て、相似の関係にある図形を見つけることがポイントとなります。
　まず三角形ＥＦＨと三角形ＤＡＨが相似の関係であることから、ＤＨ：ＨＥは三角形ＥＦＨと三角形ＤＡＨの相似比である4：2＝2：1と求められます。
　次にＤＩ：ＩＥを求めるにあたって、もとの図のままでは相似の関係が見つかりません。そこで右の図のように、ＡＧとＢＣを延長して交わる点をＪとすると、三角形ＡＤＩと三角形ＪＥＩが相似の関係になり、相似比が4：(2＋1＋2)＝4：5なので、ＤＩ：ＩＥ＝4：5となることがわかります。
　ここからの仕上げがこの問題の肝となります。ＤＥにおいてＤＨ：ＨＥ＝2：1、ＤＩ：ＩＥ＝4：5から、下の図のように比の関係を整理することができます。

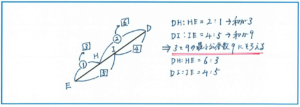
　2つの異なる比を統一するために、2：1の2＋1＝3と、4：5の4＋5＝9の最小公倍数である9に値をそろえて、ＤＨ：ＨＥ＝2：1＝6：3とします。これにより、ＤＥの長さが9とすることができ、ＤＩ：ＩＨ：ＩＥ＝4：2：3と求められるのです。
　相似の関係にある図を見つけ、比を和の最小公倍数にそろえるという流れは入試でもよく問われますので、しっかり理解しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。