　早稲田アカデミー・四谷大塚新6年生の皆様、偏差値アップのポイントは解き方の幅を少しでも広げておくことです！場合の数では公式を覚えるだけでなく、それを組み合わせて使うことが求められます。また平面図形では「高さの比」を効果的に使うことで、難問でも正解に行き着くことができます。まずは各単元のポイントとなる解き方を覚えて、問題演習を繰り返す中で、なぜその解き方になるのかについて、理解をしっかり固めてください。予習シリーズの「必修例題」で解き方を固めたうえで、「練習問題」に取り組み、間違えた問題、解法が浮かばなかった問題で解説を読んでもう一度解き直すサイクルで進めてみましょう。解法が増えることでテスト会場でも落ち着いて問題に取り組むことができ、培った力を存分に発揮して偏差値ジャンプアップを実現させることができます！

　早稲アカ・四谷大塚新5年生の皆様、得点力を大幅にアップさせるためには、図を活用すること、そして図形への着眼点を増やすことがポイントです！特に平均で活用する面積図は、これから様々な単元で大活躍する必須アイテムとなります！線分図とともに欠かせない武器ですので、かき方をしっかりとマスターしましょう。平面図形では等積変形を覚えてください。この考え方は来年度6年生になって面積の応用問題を攻略するうえでは、不可欠な要素となります。これらの考え方、解き方を今のうちに確実に習得して、普段の演習、そしてテストを通して頭の中に浸透させましょう。それができれば、来年度6年生になってからの算数の偏差値で、抜群の安定感を達成することができます！

　今年度最初の大事な組分けテストです！そこで今回は、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から新6年生、新5年生ともに第5位から第1位までのランキングのかたちにまとめました。ぜひクラスアップを実現してください！応援しています！
　さらに、このメルマガの新6年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、今年度最初の組分けテストの偏差値を別次元にまでアップさせることができます。
予想問題はこちらのページで無料公開します！

《新６年　第1回組分けテスト》

【第5位　N進法：問題文で使われる表現からN進法の問題であると気付けますか？】

　N進法は2つの段階に分けて練習すると効果的です。1つ目の段階は、N進法の基本を理解して「N進法⇒10進法」、「10進法⇒N進法」の計算を迷わずにできるようにすることです。単純に「2進法の1011を10進法に直しなさい」、「10進法の75を3進法に直しなさい」といった計算を繰り返します。ちなみに前者の答えは「11」で後者の答えは「2210」です。
　2つ目の段階は問題で使われているN進法に気付いて、それを使い問題を解くことです。これは「何種類の数字を使っている」、「いくつのときに繰り上がっている」といったことから考えられます。次の問題を使って、2つ目の段階を練習してみましょう。

　「4種類の数字｛0、1、2、3｝を使って表すことができる1以上の整数を、次のように小さい順に並べました。
　　1、2、3、10、11、12、13、20、21、……
このとき、1230は何番目ですか。また、150番目の数はいくつですか。」

という問題を考えてみましょう。
　まず問題を見て、「4種類の数字を使っている」「4個集まると繰り上がる(3→10、13→20で確認できる)」ことから、4進法であることがわかります。
　4進法は一番右の位が「1の位」で、1が4個集まると繰り上がることから右から2番目の位は「4の位」になります。同様に、4が4個集まると繰り上がることから右から3番目の位は「16の位」、16が4個集まると繰り上がることから右から4番目の位は「64の位」となっています。したがって、4進法の1230を10進法に直すと 64×1＋16×2＋4×3＋1×0＝108 となるので、108番目と求まります。
　次に150番目の数を求めます。4進法ですから4個ずつの組を作って考えます。
150÷4＝37…2　← 4が37個できて1が2個余っている
37÷4＝9 …１ ← 16(4を４個組にした)が9個できて4が1個余っている
9÷4＝2 …1 ← 64(16を4個組にした)が2個できて16が1個余っている
以上のことから、10進法の150を4進法で表すと、2112と求まります。
　このように問題を読んだ時の着眼点がわかってくるとN進法に気付き易くなります。いろいろな問題で試してみてください。

【第4位　規則性：図をかいて内容を整理すると規則が見えてきます！】

　規則を図にまとめて目で見えるようにすると、一気に問題が解きやすくなることが多いです。規則は問題によって様々です。はじめは自分なりの図で構わないので手を動かしながら試行錯誤してみましょう。かいているうちに何かに気付くかもしれません。

　「ビンに入ったジュースを37本買いました。この店では空きビン4本でジュース1本と交換してくれます。このとき、最も多くて何本のジュースを飲むことができますか。また、70本のジュースを飲むためには、少なくとも何本のジュースを買えばよいですか。」

という問題を考えてみます。
　はじめの問題の条件を図にまとめると(図1)のようになります。

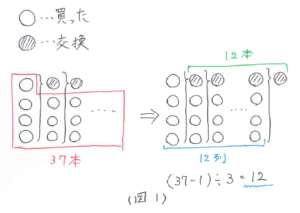
　37本買ったので (37－1)÷3＝12、このとき最後の列が4本になるので新しく1本交換できます。したがって交換したジュースは全部で12－1＋1＝12(本)とわかります。よって、飲むことができるジュースは最も多くて 37＋12＝49(本) と求まります。
　2つ目の問題の条件を図にまとめると(図2)のようになります。
　

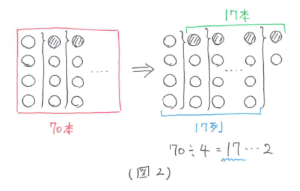
　全部で70本飲むので 70÷4＝17…2、このことから交換したジュースは全部で17－1＋1＝17(本)とわかります。よって、少なくとも 70－17＝53(本)のジュースを買えばよいことがわかります。

【第3位　場合の数：公式は覚えるだけでなく、どの場面で使えるかまで考えましょう！】

　場合の数では順列や組み合わせを求めるときに便利な公式があります。公式を使うためには前提となる条件が必要なので、公式が使える場面なのかしっかり考えることが重要です。

　「白石が3個と黒石が4個あります。この7個の碁石を横1列に並べるとき、全部で何通りの並べ方がありますか。」

という問題を考えてみます。
　この問題で多い誤答は、7個の碁石を並べるので 7×6×5×4×3×2×1＝5040(通り)という答えです。ここで注意すべき点は、順列や組み合わせの公式が使えるのは「すべて異なる」ときだという点です。白石3個は見分けがつきません(もちろん黒石の4個も)。公式がそのままでは使えないので、少し違った考え方をします。
　碁石では区別できないので他に区別できるものを探します。すると、碁石を横1列に並べることから、碁石を並べる「場所」が左から1番目、2番目……、7番目と区別できることがわかります。これを利用して7個の異なる「場所」から白石を並べる3個の「場所」を選ぶという考え方ができます。したがって、7×6×5÷(3×2×1)＝35(通り)と求まります。

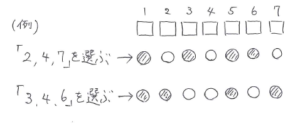
　式だけ見ると簡単に見えますが、式の意味も理解しているといろいろ応用ができます。例えば、「1、1、1、2、2の5つの数字を並べてできる5桁の整数は何通りか。」という問題も同じように、5個の異なる「場所」から数字の2を並べる2個の「場所」を選ぶと考えて、5×4÷(2×1)＝10(通り)とすぐに求めることができるようになります。大変便利な考え方なので練習して確実に身につけましょう。

【第2位　和と差に関する問題：典型題の練習には予習シリーズの「練習問題」を！】

　　次の問題を考えてみましょう。

　「A、B、C、Dの4人でゲームをしました。それぞれの得点は小さい方から、A、B、C、Dの順になりました。また、2人ずつの得点の合計が、25、32、□、38、△の5種類になりました。このとき、□と△を求めなさい。ただし、4人の得点はすべて整数であるものとします。」

　得点はA＜B＜C＜Dとなっているので、2人ずつの得点の大小は、
　　A＋B＜A＋C＜A＋D≦B＋C＜B＋D＜C＋D
　または
　　A＋B＜A＋C＜B＋C≦A＋D＜B＋D＜C＋D
になります。ここで重要なことは、小さい方から2つと大きい方から2つは、組み合わせが必ずわかるという点です。A＋B＝25、A＋C＝32、B＋D＝38、C＋D＝△とわかるので、A＋B＋C＋D=32＋38＝70 となり△＝70－25＝45 と求まります。
　また、4人から2人を組にすると得点の合計は 4×3÷2＝6(種類) できるはずですが、この問題では5種類しかできていません。このことから、A＋D＝B＋C だとわかります。したがって、□＝70÷2＝35 と求まります。
　この問題のような典型的な問題は、ポイントを知っているかいないかで、問題に使う時間が格段に違います。予習シリーズの練習問題には典型的な問題が数多くあるので、繰り返し練習して身につけていきましょう。

【第1位　平面図形：三角形の面積の比と高さの比の関係を利用できていますか？】

今回紹介したい考え方は「底辺が等しい三角形の面積の比と高さの比は等しい(※)」というものです。

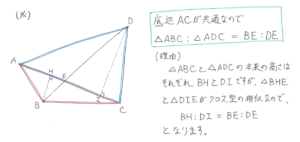
　この考え方が使えると補助線の引き方がわからない問題や、相似が発見し難い問題などで別の見方ができるようになり、問題が解き易くなります。次の問題で練習してみましょう。

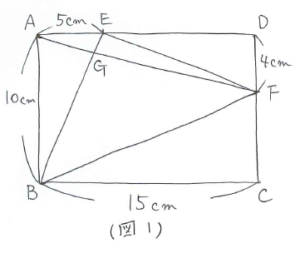
　「(図1)のような長方形ABCDがあります。AB＝10cm、BC＝15cm、AE＝5cm、DF＝4cmのとき、BG：GEとAG：GFを求めなさい。」

　これまでしっかりと学習してきたお子さんであれば、BEやAFを延長してクロス型の相似を使うことが考えられると思います。もちろんそれでも求められますが、今回は(※)の考え方を使って解いていきます。
　まずBG：GEを考えます。(図2)のようにAFを共通の底辺と考えると(※)より、BG：GE＝三角形ABF：三角形AEF＝(10×15÷2)：(5×4÷2)＝15：2 と求まります。

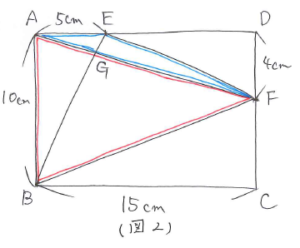
　次にAG：GFを同じように考えて求めます。(図3)のようにBEを共通の底辺と考えると(※)より、AG：GF＝三角形ABE：三角形FBE＝(10×5÷2)：｛10×15－(10×5÷2＋15×6÷2＋4×10÷2)｝＝5：12 と求まります。
　　

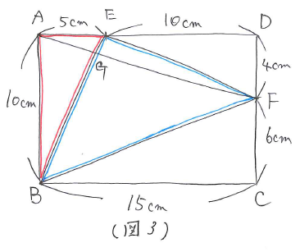
　平面図形の問題はいろいろな解き方ができることが多いです。問題によっては普段自分が使っている解き方では解き難い問題もあります。そのため、いくつかの解き方を用意して問題によって使い分けられると、対応できる問題が増えておすすめです。少しずつ解き方を増やしていきましょう。　

《5年　第1回組分けテスト》

【第5位　割合の基本：問題文から正確に式を立てられていますか？】

　割合はしっかり文章を読んで、「割合」「もとにする量」「くらべる量」を探し出すことができれば難しくありません。しっかり見つけられるようになるまで練習をしていきましょう。
　まずは短い問題から。

　「300円の2倍は□円です。」

この問題では答えがすぐに600円と分かりますが、じっくり文章を見ていきます。
　最初に注目するのは「割合」です。「割合」を表す言葉は「△倍」や「A/B」など文章の中から見つけ易いです。この問題では「2倍」です。
　次に探すのは「もとにする量」です。先ほど見つけた「割合」の前に「の」という助詞が入っています。その「の」の前が「もとにする量」になります。
　ここまで考えて式を立てます。「くらべる量＝もとにする量×割合」なので、300×2＝600となります。
　しっかり考えるとこうなりますが、実は簡便的なやり方もあります。それは問題文の「もとにする量」と「割合」の間にある「の」を「×」に置き換えると式が出来てしまうというやり方です。
　ほかの問題でも試してみましょう。

　「お母さんの年令は30才です。太郎君の年令はお母さんの年令の1/5です。太郎君の年令は何才ですか。」

　順番に考えていきます。「割合」は「1/5」です。その前に「の」があり、さらにその前の「お母さんの年令」が「もとにする量」になります。したがって、「の」を「×」に置き換えて式と立てると、30×1/5＝6(才)となります。
　もう1題やってみます。

　「5年1組の生徒が3人欠席しました。これはクラス全体の1/10にあたります。クラスの人数は何人ですか。」

　まず「割合」は「1/10」です。その前に「の」があり、さらにその前の「クラス全体」が「もとにする量」になります。したがって、「の」を「×」に置き換えて式を立てます。クラス全体の人数を□とすると、□×1/10＝3という式が立てられます。逆算をして、□＝3÷1/10＝30(人)と求まります。
　あくまでも簡便的なやり方なのですべての問題で使えるわけではないですが、基本的な問題では威力を発揮します。ぜひほかの問題でも試してみてください。

【第4位　図形の面積：等積変形の解き方をフル活用できていますか？】

　図形の面積を求めるときに、形を上手く変えることができると問題が解き易くなる場合があります。形を変える代表的な方法が等積変形です。次の問題を使って、練習してみましょう。等積変形については、以下の図を参照してください。

　「(図1)のような長方形ABCDがあります。斜線部分の面積が20平方cmのとき、Xの長さは何cmですか。」

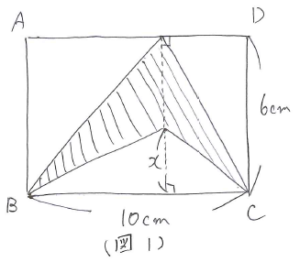
　等積変形を使って形を変えます。平行になっている場所に注意して変形すると(図2)のようになります。面積から三角形の高さを求めると 20×2÷10＝4(cm)となり、X＝6－4＝2(cm)と求まります。
　　
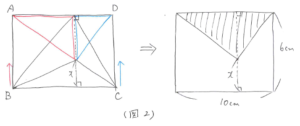
　等積変形を使わないと求められない問題もありますので、しっかりと練習しておきましょう。

【第3位　約数・倍数：書き出しと式の両方を使いこなせていますか？】

　約数・倍数の問題では、問題文にある数字を組み合わせても答えは出ません。順序良く考える練習をしながら、少しずつ量の多い問題が解けるようにしていきましょう。

　「5で割ると3余り、6で割ると5余る数があります。小さい方から数えて5番目の数はいくつですか。また、400に一番近い数はいくつですか。」

という問題を考えてみましょう。
　まず「5で割ると3余る数」を書き出します。このとき、一番小さい数が3であることに注意しましょう(3÷5＝0…3)。
　3、8、13、18、23、28
このとき、5と6の最小公倍数である30を超えることはありません。
　続いて「6で割ると5余る数」を書き出します。こちらは同じ数が出るまで書けばいいでしょう。もちろん一番小さい数は5です。(5÷6＝0…5)
　5、11、17、23
調べた結果、23が「5で割ると3余り、6で割ると5余る数」の中で一番小さい数だとわかります。あとは、23から5と6の最小公倍数の30ずつ数が増えていくので等差数列になっています。
　23、53、83、……
したがって、小さい方から5番目の数は 23＋30×(5－1)＝143 と求まります。
　次に400に一番近い数を求めます。逆算の式をたてて、23＋30×(□－1)＝400 として計算してみます。□＝(400－23)÷30＋1＝12.5… となるので、等差数列の12番目辺りだと見当をつけて調べます。 23＋30×(12－1)＝353、353＋30＝383、383＋30＝413 となり、400に一番近い数は413と求まります。
　書き出したり、調べたりする時間は練習すれば減らすことができます。解き方が決まっている問題で悩まないように、しっかりと考え方を身につけましょう。

【第2位　平均の面積図：面積図のかき方を徹底的に練習し、理解しましょう！】

　平均の問題で「数量の合計＝平均×個数」を使って合計が計算できないときは、面積図を使うと解き易いです。面積図のかき方は、たてに「平均」を書き、横に「個数」を書きます。すると、たて×横で計算できる面積が「数量の合計」になります。

　「あるお店でノート買います。ノートは20冊までは1冊120円ですが、20冊を超えると１冊につき90円になります。1冊あたりの値段が100円になるのはノートを何冊買ったときですか。」

　条件を図にかきこむと、(図1)のようになります。
　

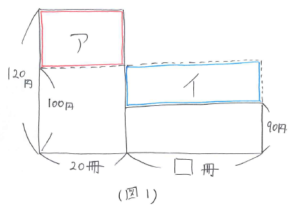
　平均とは「平らに均す」ことですから、(図1)のアの部分とイの部分の面積が等しくなっています。よって、(120－100)×20＝(100－90)×□、□＝40(冊)となります。この40冊は90円で買った冊数なので、買ったノートは全部で20＋40＝60(冊)と求まります。
　このように面積図を使うとあっさり求めることができます。数量の合計を計算しようとして行き詰まったら、すぐに面積図を思い出して使っていきましょう。

【第1位　割合の応用：線分図を用いれば複雑な問題も攻略できます！】

　もとにする量が途中で変わる問題では、文章をよく読み、何をもとにしているのか間違えないようにしましょう。ポイントはやはり「割合」の前の「の」のさらに前が「もとにする量」になるという点です。問題を解いて確認をしてみましょう。

　「ある本を1日目に全体の3/5より7ページ少なく読み、2日目に残りの4/7より10ページ少なく読んだところ、37ページ残りました。この本は全部で何ページありますか。」

　文章をよく読むと、3/5のもとになっているのは「全体」で、4/7のもとになっているのは「(全体から1日目の分を引いた)残り」だとわかります。このことを考えて、丁寧に図をかくと(図1)のようになります。
　　　

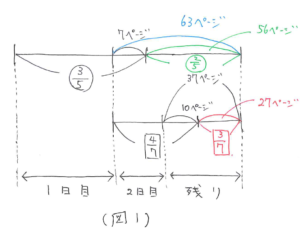
　全体から1日目の分を引いた残りは(37－10)÷(1－4/7)＝27÷3/7＝63(ページ)と計算できます。よって、全体は(63－7)÷(1－3/5)＝56÷2/5＝140(ページ)と求まります。
　割合の問題は文章が複雑になっても、「割合」→「もとにする量」と考えることは変わりません。その基本方針のもとに、しっかり練習していきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。

今みんなが読んでいる記事はこちら

全てグノーブルで勝つ方法 SAPIXで勝つ方法日能研で勝つ方法早稲田アカデミー・
四谷大塚で勝つ方法入試で狙われる時事問題合格に導く魔法の本棚わが子を早慶へわが子を医学部へママとパパの勉強部屋受験情報ここだけの話模試と過去問の鉄則中学受験は勉強法が９割ブラタモリクイズ！

メールマガジン登録は無料です！

頑張っている中学受験生のみなさんが、志望中学に合格することだけを考えて、一通一通、魂を込めて書いています。ぜひご登録ください！メールアドレスの入力のみで無料でご登録頂けます！

メールマガジン登録はこちら

登録解除の場合はこちら

メールマガジン宝箱 Mail magazine