メールマガジン宝箱 Mail magazine

　サピックス6年生の皆様、今回のマンスリーテストでの偏差値アップのポイントは、ズバリ比を使いこなすことです。平面図形での面積比や相似、立体図形での体積比はもちろん、割合の問題でも比と図を駆使して問題内容を整理できるかどうかが得点に大きく影響を及ぼします。また、グラフの問題でも数値を使ってただ計算するよりも、比を利用してグラフを読み取る方が、スピードでも正確さでも圧倒的な優位に立てます。比を利用した解法は、実際の入試問題でも大いに必要とされます。算数で入試の合格ラインを超えるためには、比を使いこなせるようになっておくことが必須の条件なのです！ただ問題に正解するだけでなく、比を的確に使えたかどうかまでチェックする習慣をつけておきましょう！
　ランキングでご紹介する5つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介するランキングと予想問題を照らし合わせれば偏差値が飛躍的にアップします！頑張ってください！
予想問題はこちらのページで無料公開します！

【第5位　場合の数：組合せを求める前の「場合分け」が正確にできていますか？】

　場合の数の問題の中で、並べ方や組合せの数を求める基本パターンから一歩進んで、まず「場合分け」をしなくてはならないケースがあります。6年生の4月にもなると、そうした応用問題が出される可能性が圧倒的に高くなります。そうした問題にはどのように対応すればよいでしょうか。「場合分け」を正確にするためには、どのような対策が必要なのでしょうか。
　ポイントは、図や表を使ってかき出しをすることです。場合の数を頭の中だけで処理しようとすると、本来選ぶべき場合を見逃してしまうことが多く起こります。簡単な図で構いません。むしろ簡単にかき出さなければ余計な時間がかかってしまいますので、的を絞ったかき方が必要になります。
　例えば次のような問題にはどのように対応すればよいでしょうか。　

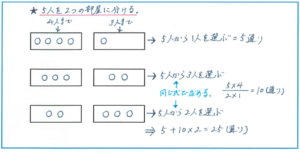
　解法の流れとしては、「月の間」と「星の間」に分かれて泊まる方法が何パターンあるのかをまずは考えます。そして、それぞれのパターンについて何通りの泊まり方になるのかを求めることになります。
　この最初のパターン分けを上の図のように進めるとスムーズに内容が整理できます。注意すべきは、「星の間」には3人までしか泊まれませんので、「月の間」に1人、「星の間」に4人のパターンは起こりえないこと。その点を注意すればパターン分け自体は難しくないでしょう。
　あとは計算を慎重に進めていくのですが、以下の2点に気をつければ、より楽に計算ができます。
①「月の間」に3人、「星の間」に2人と分ける場合と、「月の間」に2人、「星の間」に3人と分ける場合は同じ数になる。
②5人から3人を選ぶのは、5人から2人を選ぶことと同じなので、小さい数の方で計算する（ではない方で計算する、のパターンです）。
　どちらも基本的な内容ですので、間違いなく対応できるように、ここでつまずいてしまう場合は、5年のテキストに戻って急ぎ復習を進めましょう。計算結果は以下の通りです。
「月の間」に3人・「星の間」に2人
「月の間」に2人・「星の間」に3人
→どちらも、(5×4)/(2×1)＝10（通り）
「月の間」に4人・「星の間」に1人
→「星の間」に泊まる1人を選べばよいので5通り
　よって、10×2＋5＝25（通り）となります。
　選ぶべきパターンを逃しているのではないか、というモヤモヤとした不安を抱いてしまいがちなことから場合の数を苦手に感じてしまうケースが多く見られます。演習する問題数を多くすることが第一ではありますが、そこで今回のように図を活用して、少しでも不安を払拭する手がかりがつかめれば、場合の数をむしろ得意分野にすることもできます。ぜひ手を動かして、問題内容を整理、理解するようにしてください。

【第4位　速さのグラフ：速さ・時間・道のりの比の関係をグラフから読み取れていますか？】

　速さのグラフの問題では、グラフから速さや時間をただ読み取る段階だけでなく、速さ・時間・道のりの比の関係をグラフから読み取ることまで求められるようになります。つまり、時間が一定であれば速さの比が道のりが比になること、道のりが一定であれば速さと時間は逆比の関係になることを、瞬時にグラフから読み取れるようになっておく必要があるのです。

　上のグラフに示したような、グラフのどの部分の長さに比の関係が見られるのかを確実に理解しておいてください。当たり前のように思われるかもしれませんが、グラフから比の関係を瞬時に読み取ることができるようになっておけば、問題を解くために必要な材料を確実に手にすることができ、問題を速く正確に解けるようになるのです。ほんの些細なことでも、そこがわかっているかいないかの差が偏差値の差となって現れるパターンのひとつです。しっかり確認をしてテストに臨むようにしましょう。

【第3位　立体図形：面積比と高さの比から体積比を求める方法を理系できていますか？】

　今回のマンスリーの立体図形では回転体が範囲に含まれることから、円すいの問題が出される可能性が高くあります。例えば図のような円すい台から円すいをくり抜いた立体の体積を求める際に、比を使うと計算が圧倒的に楽になることがあります。
　次の問題にはどのように対応すればよいでしょうか。

　ここで比を使わずに、円すい台の体積を求め、そこからくり抜かれた円すいの体積を引くことでも正解に行き着くことはもちろんできます。ただ、いかに3.14計算をまとめるといった工夫をしても、大きな小数の引き算になりますので、間違えるリスクは回避できません。
　そこで以下のように各部の体積を底面積の比と高さの比のかけ算で表せば、計算しやすくなります。
最も大きな円すいの体積：
4×4＝マル16
円すい台の上の想定される円すいの体積：
1×2＝マル2
くり抜く円すいの体積：
1×1＝マル1
求める部分の体積はマル16－(マル2＋マル1)＝マル13
マル1はくり抜く円すいの体積なので、2×2×3.14×4＝16×3.14
　よって求める体積は16×3.14×13＝208×3.14＝653.12（立方cm）となります。
3.14計算が大きくはなりますが、3.14×1ケタの数の結果を覚えておけば、筆算は楽に進めることができます。平面図形の面積だけではなく、体積でも比を活用できるように練習を重ねましょう。

【第2位　平面図形：面積比の基本パターンを駆使できていますか？】

　平面図形の問題で面積比を求める際に基本パターンをいかに有効に駆使するかが、難問対策には必要不可欠なステップとなります。
　例えば下の図のような三角形の2辺を通る直線で分けられた部分の面積を比のかけ算で求めるパターン。図のように2辺をはさむ頂点が上にあるような場合であればすぐに解法が浮かぶとしても、そのかたちが変わっても対応できるかどうかが、サピックスの6年生のテストで偏差値をアップさせるうえでは必須となります。

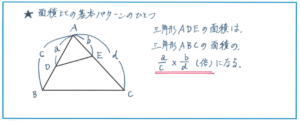
　それでは、次のような問題にはどのように対応すればよいでしょうか。

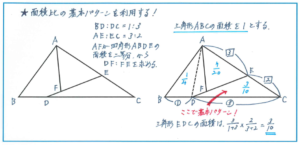
　この問題では、ＤＦ：ＦＥの長さの比を面積比から求めるために、三角形ＡＤＥをつくるべく、補助線ＡＤをひくことが重要になります。そして、四角形ＡＢＤＥの面積を用いることになるため、前提条件として三角形ＥＤＣの面積が必要になるのです。ここで先に挙げました基本パターンを活用します。三角形ＡＢＣの面積を1として、長さの比をもとに図形の面積を割合で表していきます。
　ＢＤ：ＤＣ＝1：3、ＡＥ：ＥＣ＝3：2より三角形ＥＤＣの面積は3/4×2/5＝3/10
　三角形ＥＤＣは、先に挙げた基本パターンを横に倒したかたちになっています。そのようにかたちが変わっても図を見てすぐに基本パターンを使えるようになっておくことが、これから難問を攻略するためには求められます。そのために、まずは基本パターンを丸覚えするのではなく、辺の長さの比と面積の比の関係を理解したうえでパターンを覚えることが必要です。そのうえで、多くの図形問題を解き、そこでパターンが使えるかどうかを検証する時間を持つようにしましょう。その積み重ねが、基本パターンを駆使する技術を向上させます。
　問題に戻ると、四角形ＡＢＤＥの面積は、1－3/10＝7/10であり、この面積がＡＦで二等分されますので、三角形ＡＦＥの面積は7/10×1/2＝7/20になります。三角形ＡＢＤの面積は、1－3/4＝1/4ですので、三角形ＡＤＥの面積は7/10－1/4＝9/20です。よって、ＤＥ：ＦＥ＝三角形ＡＤＥの面積：三角形ＡＦＥの面積＝9/20：7/20＝9：7より、ＤＦ：ＦＥ＝9－7：7＝2：7と求められます。
　辺の長さの比を面積比から出す流れもしっかり確認しておきましょう。

【第1位　割合（やりとりの問題）：比と図を用いて状況を整理できていますか？】

　割合の中で、以下のようなやりとりの問題があります。なお、分数は分子/分母のかたちで表記します。

　このタイプの問題で注意すべきポイントは以下の3点です。なお、○の中に数字が入る記号がメルマガでは表せませんので、マル1のかたちで表記します。
1.比を用いて所持金を記号化する。
2.合計金額が変わらないことを利用する。
3.やりとりを図で整理する。
　まず2人の所持金の関係について、太郎君が次郎君の2倍とありますので、太郎君をマル2、次郎君をマル1と置くことができるのですが、2人の合計がマル2＋マル1＝マル3となり、最後に2人の所持金が等しくなるところで、それぞれの所持金がマル3/2と分数で表されることになってしまいます。そこでここでは太郎君をマル4、次郎君をマル2と置くことにします。このような数の置き方の工夫は計算を楽にする効果がありますので、常に注意しておくようにしましょう。これが最初のポイントになります。
　次に、2人の合計金額が変わらないことを利用すると、その合計金額はマル4＋マル2＝マル6で変わらず、最終的な2人の所持金はマル6÷2＝マル3と表すことができます。ここからさかのぼってやりとりを整理するのですが、ここで最後のポイント、図の活用が必要となります。
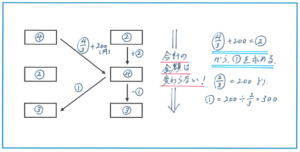
　上記のように2人の所持金を記号化した数字を図の枠の中にかき込み、やりとりされた金額を矢印の近くにかき込むと、お金の動きが視覚的にも理解できます。
　次郎君は、最後に自分の所持金の1/4を渡した結果、所持金がマル3になったので、その前にはマル3÷(1－1/4)＝マル4を所持していたことがわかります。最初の次郎君の所持金がマル2なので、次郎君は最初に太郎君からマル4－マル2＝マル2を渡されました。太郎君は「はじめの所持金の1/3より200円多い金額を次郎君に渡した」と問題文にありますので、ここで以下の式が成り立ちます。
　マル4/3＋200＝マル2
　ここからマル2－マル4/3＝マル2/3が200円に相当することがわかりますので、マル1が200÷2/3＝300（円）と求められます。
　あとは問題で最終的に何を求めるかに最大限の注意を払ってください。ここで間違ってしまってはこれまでの積み重ねが水の泡となってしまいます。求めるのは「はじめの太郎君の所持金」ですので、マル4の値となります。300×4＝1200より答えが1200円と導き出せます。
　割合の問題では比を利用して数字を記号化するケースがとても多くあります。まずはそのかたちに慣れ、そしてやりとりの問題では「どの量が変わっていないか」に注目するようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。