メールマガジン宝箱 Mail magazine

　6年生の5月末になると、テストの難度が徐々に上がってきます。平面図形ではいくつかの図形が複合する複雑な問題が多くなり、割合や速さの問題では問題文のボリュームが増えるなど、問題を見てすぐには解法が浮かべることが難しくなってくるのです。こうした問題を確実に正解するためには、頭の中だけで問題を処理するのではなく、問題への書き込みや式を見やすく書き並べるなどの工夫をして、問題内容を視覚的に整理することがポイントになります。例えば平面図形の角度の問題では、補助線を引いて図形の中から二等辺三角形や正三角形を見つけ出し、その性質を利用することで解答の方針が固められます。また、売買損益で売り値が変化する問題では、式を見やすく書き並べることで変化の様子が正確に把握することができます。手を使って問題内容を整理する流れを今からしっかり理解しておけば、応用問題での正解が圧倒的に増え、偏差値の大幅アップにつながります！
これからご紹介する3つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！　　
さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題を合わせれば偏差値を別次元にまでアップさせることができます！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：角度の問題で二等辺三角形を見つけられていますか？】

　平面図形の問題では相似や面積比などの問題だけでなく、角度を求める問題もテストで頻出ですが、6年前期になると図形が複雑になり、角度を求める式が簡単には立てられなくなってきます。そうした問題では、等しい辺の関係を見つけて、二等辺三角形や正三角形の性質を活用すれば解答の糸口をスムーズに見つけられるようになります。例えば次のような問題にはどのように対応すればよいでしょう。

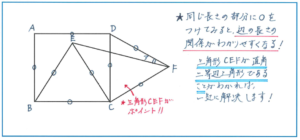
　求める角度は角DFEの大きさですが、その角度に注目しているだけでは解法を方針が立ちません。問題で与えられた条件、特に三角形の辺に関する条件を整理してみましょう。
　三角形BCE、CFDが正三角形なので、辺BC、CE、EBの長さが等しく、また辺CD、DF、FCの長さが等しくなります。そして四角形ABCDが正方形なので、辺BC、CDの長さが等しくなることから、辺BC、CE、EB、CD、DF、FCはすべて同じ長さであることがわかります。そこから、三角形CEFはCF＝CEの二等辺三角形になります。この二等辺三角形を見つけることが、この問題を解くためのポイントです。
　ここからは角度に注目して解き進めていきましょう。角DCE＝90－60＝30(度)、角ECF＝60＋30＝90(度)より三角形CEFは直角二等辺三角形となり、角CFEの大きさが45度であることがわかり、求めるアの角DFEの大きさが60－45＝15（度）と求められます。
　今回のような正方形などの正多角形と正三角形が組み合わさったタイプの問題だけでなく、円やおうぎ形の問題でも二等辺三角形を活用することが解答のポイントとなることが多くあります。等しい辺の関係を見つける意識を強く持つようにしましょう。

【直前チェックポイント２：売買損益の利益を売り上げと仕入れ値で考えることはできていますか？】

　割合や比の問題では解答に使う条件が増え、問題文も長くなるケースが増えてきます。そうした問題では条件が多いからといって戸惑うことなく、ひとつひとつを順に整理して行けば正解に行き着くことができます。例えば次のような売買損益の問題にはどのように対応すればよいでしょうか。

　売り値の設定が初日、2日目、3日目と変動するので1日ごとの利益に注目すると混乱してしまいます。このような問題では、仕入れ値と売り上げの合計を比較する方針で内容を整理すると正解に行き着くことができます。仕入れ値、初日の売り上げ、3日目の売り上げを書き出して、売り上げの総額から2日目の売り上げを求めることにしましょう。
　まず仕入れ値は1個1000円で100個ですので、1000×100＝100000（円）、3日間の総利益が18000円なので、3日間の総売り上げは、100000＋18000＝118000（円）になります。
　初日の売り上げは、商品1個の売り値が1000×1.25＝1250（円）で、4割が売れ残ったので6割にあたる60個を売ったので、1250×60＝75000（円）。
　3日目に売った個数は100－(60＋30)＝10個で、仕入れ値の1000円で売ったので1000×10＝10000（円）より、2日目の売り上げ金額は、118000－(75000＋10000)＝33000（円）になります。
　ここまでの計算が正確にできるように、金額の書き出しを見やすくするように注意しましょう。
　2日目には30個販売しましたので、1個あたりの売り値は、33000÷30＝1100（円）となります。定価は1250円なので、1100÷1250＝0.88より、定価の1割2分引きと答えが求められます。
　式の数自体は多いですが、解き進め方はいたってシンプルです。上記のように価格の計算を正確に行い、見やすく書き出せば、正解に行き着くことは決して難しくありません。ていねいに取り組みましょう。

【直前チェックポイント３：場合の数は最後の最後まで慎重に取り組みましょう！】

　場合の数の問題が難しく感じる理由のひとつとして、見直しがしづらく、最後の最後まで慎重に取り組まなければいけないことが挙げられます。割合や速さの問題、そして図形の問題では、求めた答えを問題に当てはめて答えが正しいかどうかを確かめることができますが、場合の数ではその見直し方では答えを確かめられないことがあります。それだけに慎重な取り組みが不可欠になるのです。
例えば次のような問題です。

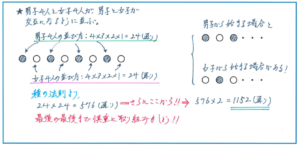
　男子4人の並び方、女子4人の並び方の求め方は基本的な内容ですので、ここが曖昧な場合は、5年のテキストに戻って復習をしておきましょう。男子4人の並び方は4×3×2×1＝24（通り）、女子4人の並び方も同じく24通りとなります。ここから積の法則を使って、24×24＝576（通り）となることまでは正確に求められるようにしておきましょう。場合の数での和の法則と積の法則の使い分けを間違わないように注意してください。ここから最後の詰めです。男子と女子を交互に並べるときに、男子から始める場合と女子から始める場合があるので、2倍をして576×2＝1152（通り）になります。
上記のような図をかくと、最後の2倍を忘れないような意識を強く持つことができます。場合の数は頭の中だけで解くのではなく、書き出しや図を使って、視覚的にも内容を整理でする習慣を身につけておけば、問題の正答率が大幅にアップします！

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。