メールマガジン宝箱 Mail magazine

　6月マンスリーは場合の数や点の移動、グラフ問題といった得点しづらい単元が多く出題されます。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
　予想問題はこちらのページで1週間限定で無料公開します！

【第5位　場合の数（サイコロの目）：目の和を正しく場合分けできていますか？】

　場合の数では、並べ方や組み合わせの計算をする前段階で、正しく場合分けをする必要があります。この場合分けができてしまえば、計算も進めやすくなり、問題の正答率も大きくアップします！場合分けをする際に、例えば3の倍数や4の倍数のきまりといった数の性質の知識を使うケースが多くあります。例えば次のような問題です。

　問題を解くには次のようなステップを踏んで進んでいきます。
① 6の倍数のきまりを確認。
② 1から6までの数を足して6の倍数になるケースをピックアップ。
③ 各ケースが何通りあるのか計算で求める。
　まずは6の倍数は3の倍数の中の偶数ですので、3の倍数のきまりである「各位の和が3の倍数」であることを満たす偶数を選べばよいことになります。
ポイントとなるのは②。ここで選びもれがないように気をつけなければいけません。そのためには選んだケースをしっかり書き出しておきましょう。頭の中だけで処理しようとするとミスにつながります。最後の③の計算では、3つの数の組合せによって式が異なることに注意すれば、6＋3＋1＋6＋6＋3＋6＋1＋3＋1＝36（通り）と、式は長いですが計算自体は難しくありません。
　場合の数は見直しがしづらいこともあり、ミスに気づかないままに解き進めてしまうことが多くあります。それを防ぐためにも、②でしたように、該当するケースを書き出して、視覚的なチェックができるようにしましょう。

【第4位　場合の数（ぬり分けの問題）：計算に入る前にケースを書き出すと解きやすいです！】

　場合の数の中でも色分けの問題は、どのようなケースがあてはまるのかがイメージしづらいこともあり、苦手とされる生徒さんが多い単元です。対策として、問題のルールにそって、あてはまるケースをかき出してみるとよいでしょう。次のような問題にはどのように対応すればよいでしょう。

　ここで注意しなくてはいけないのが「となり合う部分には同じ色は使わないこと」という点です。4か所を3色でぬり分けるので、1色は2か所で使うことになり、ここでとなり合う部分が同じにならないような注意が必要になります。そこで、同じ色をとなり合わないようにぬり分けるケースをかき出したのが右の図です。上はＡが同じ色、下はＢに同じ色が入るかたちになります。
　この解法の利点は計算が楽なことです。ＡからＣに青、白、赤のどの色をあてはめるかについては、それぞれの場合で3×2×1＝6（通り）ずつありますから、全部で6×2＝12（通り）となります。
　図をかき出す際には時間がかかり過ぎないように、丁寧にかき過ぎないように、ラフなタッチで構いませんので、自分で見やすくなるようにしましょう。

【第3位　投票算：仮のライバルを想定する解き方はできていますか？】

　投票算の問題は、式はいたってシンプルなのですが、式を丸覚えするだけでは問題の難度が上がった際に対応できなくなります。なぜその式になるのか、その意味を確かに理解しておくことが重要な単元と言えます。
次のような問題を例に考えてみましょう。

　式のかたちを覚えていると、840÷5＝168まではすぐにかけるでしょう。ただ、ここでなぜ5で票数の合計を割るのか、この式の答えが何を表しているのかをしっかり理解しておかなければ、問題のかたちが少し変わっただけでも対応できなくなってしまいます。
　投票数の上から4位に入れば当選しますので、840÷4＝210（票）と考えてしまいがちですが、これは当選する4人以外が0票であることを前提とした、4位になるための最多の得票数であり、問題では最少の得票数を求めています。その点をとり違えないように注意しましょう。4位になるためには5位の生徒より1票でも多く獲得すればよいことになります。そこで5位になるための最多の得票数が、840÷5＝168（票）となります。5位の生徒という仮のライバルを想定して解くことになります。その5位の生徒の最多に得票する可能性があるのが168票ですので、4位になるには1票を足した168＋1＝169（票）が答えになります。
　こうした式の根拠をひとつひとつ確かにしたうえで式を暗記することで、問題の出され方が変わっても対応できるようになります。解法が理解できていれば得点源にできるのが投票算ですので、焦らずじっくり復習しておきましょう。

【第2位　点の移動：連続した動きではなく、時間ごとに点の位置を確認することがポイントです！】

　点の移動は平面図形と速さの両方の要素を持ち、またイメージがしづらい点で解きづらさを感じる手イプの問題です。点の動きを連続したものではなく、点が図形の頂点上にある時などの区切りごとに状況を把握すると、問題内容がイメージしやすくなります。
　例えば次のような問題です。

　まず直線ＰＱが辺ＡＤと平行になる状況ですが、点Ｐが辺ＣＤ上にあり、点Ｑが辺ＡＢ上にある場合か、あるいは点Ｐが辺ＡＢ上にあり、点Ｑが辺ＣＤ上にある場合のどちらかとなります。求めるのは直線ＰＱが辺ＡＤと「初めて」平行になる状況ですので、先に成立する点Ｐが辺ＣＤ上にあり、点Ｑが辺ＡＢ上にある場合に平行になれば、それが答えとなります。
　点Ｐが頂点Ｄに着いた180÷4＝45（秒後）の状況を図にしたのが右上の図です。この時に点Ｑは5×45＝225（cm）を進みますので、頂点ＢからＣに225－180＝45（cm）の地点にいます。ここで、点Ｐが辺ＣＤ上にあり、点Ｑが辺ＡＢ上にある場合に絞って考えることができるのです。
　直線ＰＱが辺ＡＢと平行になる時にＡＱ＝ＤＰになりますので、頂点Ｄから進む点Ｐの動きを点Ａからの動きに置き換えることで、点Ｐと点Ｑが出会う時点が求める時間になります。
　45秒後から後の2点の動きで考えます。点Ｐと点Ｑの動いた長さの合計が90－45＝45（cm）になればよいので、45÷(4＋5)＝5（秒後）より、出発してからは45＋5＝50(秒後)と答えが求められます。
　点の移動では、時間を追って状況を見ることで動きがイメージしやすくなることを覚えておいてください。

【第1位　変化のグラフ：立体の断面図で時間の経過を整理できていますか？】

　変化のグラフの中で、仕切りのある水そうに水を注いだ時の時間と水の深さの関係を表すグラフの問題は、立体の断面図を利用すると、変化の様子がわかりやすくなります。
　次の問題を例に考えてみましょう。

　こうしたタイプの問題を解く際には、まず立体を正面から見た断面図をかいて、水の深さの変化をとらえることが有効です。断面図をかく際には、問題の図にかき込むのではなく、ラフなタッチで構いませんので、自分でかき直すようにしましょう。その方がかき込みがしやすく、状況の理解が進みます。以下のような断面図になります。

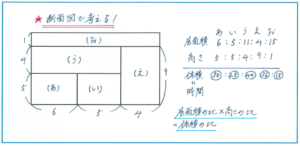
　ここで、断面図の（あ）（い）（う）（え）（お）の各部分について、右の表で整理します。底面のたての長さ（奥行き）はどこも10cmですから、横の長さの比がそのまま底面積の比になります。底面積の比と高さの比をかけ合せることで、体積の比が求められます。
　水は毎秒10立方cmの割合で注がれたので、体積の比と各部分を水で満たす時間の比は同じになります。（あ）の部分を水で満たすのにかかる時間は、6×5×10÷10＝30（秒）で、これがマル30にあたるので、マル1は1秒です。ここから、ア～オにあてはまる数は以下の通りになるのです。
　アは30、イは30＋25＝55、ウは55＋44＝99、エは99＋36＝135、オは135＋15＝150
　まずは立体の断面図で水の深さの変化を整理することを徹底的に注意してください。そこからは比を使って解くことでスムーズに正解に行き着くことができます。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。