メールマガジン宝箱 Mail magazine

　今回の5年生組分けテスト偏差値アップのポイントは、図を駆使して「速さの問題」での正答数を上げること！往復の旅人算など様々なタイプの問題で、どのような図を使えばよいのかをしっかり整理しておきたいところです。そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。　
　メルマガを読んで、速さの問題での得点力を倍増させましょう！

【第5位　平均の速さ：2つの速さを足して2で割る間違いはしていませんか？】

　今まで学習してきた「速さ」は全て「平均の速さ」です。「平均」という言葉に引きずられて「足して2で割る」というミスをしないように注意しましょう。

という問題で考えてみましょう。
　速さの公式を確認すると「速さ＝道のり÷時間」です。この問題に合わせてもう少し詳しく書くと「往復の平均の速さ＝往復の道のり÷往復にかかった時間」になります。このことから「平均」という言葉に惑わされず、いつも通り速さを求めればよいことが分かります。
　往復の道のりは 120×2＝240(km)、往復の時間は 120÷40＋120÷60＝5(時間)となるので、往復の平均の速さは 240÷5＝48(km/時)と求まります。
　もう1題やってみましょう。

　この問題も同じように「A町からC町までの平均の速さ＝A町からC町までの道のり÷A町からC町まで移動するのにかかった時間」と考えます。A町からC町までの道のり＝20＋30＝50(km)、A町からC町まで移動するのにかかった時間＝20÷5＋30÷6＝9(時間)となるので、A町からC町までの平均の速さ＝50÷9＝5・5/9(km/時)と求まります。
　速さの問題では割り切れないことも多いので、分数を使って早く計算する方法を身につけましょう。

【第4位　周回する旅人算：図を使って問題の条件をまとめられていますか？】

　周回する旅人算では、「1周の長さ÷速さの和＝出会うまでの時間」「1周の長さ÷速さの差＝追いつくまでの時間」といった公式がよく使われます。次の問題で練習してみましょう。

という問題を解いてみましょう。
　　　　

　A君が毎分100mで歩いたときに出会った地点をQ、毎分120mで歩いたときに出会った地点をR、B君の速さを毎分□ｍとして線分図にまとめると図2のようになります。
　

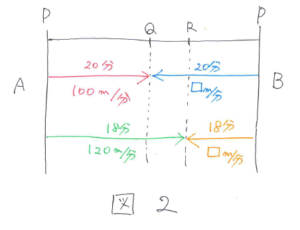
　線分図の左側から見ると、PQ＝100×20＝2000(m)、PR＝120×18＝2160(m)なのでQR＝2160－2000＝160(m)となります。
　また、線分図の右側から見ると、PQ＝□×20、PR＝□×18なのでQR＝□×20－□×18＝□×2となります。
　このことから □×2＝160となり、□＝80(m/分)とわかります。したがって池の周りの長さは (100＋80)×20＝3600(m)と求まります。
　速さの問題でも図に条件をまとめることは大切です。頭の中で問題を整理するのに非常に役立ちますので、いろいろな図を練習してみるといいでしょう。

【第3位　グラフと水量：グラフの値から体積を求められていますか？】

　容器に入った水の体積を求める方法は2つあります。1つは容器のかたちを利用する方法で「体積＝底面積×高さ」、もう1つはグラフを利用する方法で「体積＝1分あたりの水量×時間(分)」です。このように体積を求める方法が2つあるので、体積が計算できる部分に着目するのが、これらの問題を解くためのコツになります。

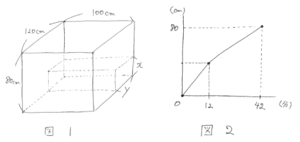
　水量の問題では、図3のような横から見た図をかいて考えると解き易いです。

　上の部分の水量はグラフから、20×(42－12)＝600(L)＝600000(立方cm)とわかります。このことから、ア＝600000÷(100×120)＝50(cm)、x＝80－50＝30(cm)と求まります。
　また、下の部分の水量もグラフから、20×12＝240(L)＝240000(立方cm)とわかり、
イ＝240000÷(30×100)＝80(cm)、ｙ＝120－80＝40(cm)と求まります。

【第2位　3人の旅人算：線分図で整理すると、解答のヒントが見えてきます！】

　3人の旅人算では、3人の中から注目する2人を決めて、その2人で旅人算の公式を使っていきます。問題を読んで条件を整理して、誰と誰に注目して旅人算の公式を使うのか考えて問題を解いていきましょう。

という問題を考えてみましょう。
　AとCが出会った場所をRとし、AとCが出会ったときにBがいる場所をSとして、図にまとめると図1のようになります。

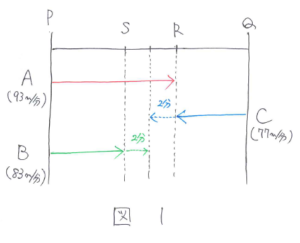
　このあとBとCが2分で出会ったことから SR＝(83＋77)×2＝320(m)とわかります。このS地点とR地点の道のりは、AとCが出会ったときの「BとCの間の道のり」と「AとBの間の道のり」という2つの見方ができます。問題にBとCが出会ったと書いてあるので「BとCの間の道のり」はすぐにわかりますが、R地点でAとCが出会っていることから「AとBの間の道のり」と気付くことができるかがポイントになります。AとBの間の道のりが320mなので 320÷(93－83)＝32(分後)にAとCが出会ったことがわかります。したがってP地点とQ地点の道のりは(93＋77)×32＝5440(m)と求まります。
　条件を図にまとめて、目で見ながら考えるようにすると効果的です。問題文を読んだだけでは気付き難いことも、目で見たらすぐに気が付くという事も多いです。繰り返し練習して身につけましょう。

【第1位　往復の旅人算：2回目に出会うまでの道のりは1回目に出会うまでの道のりの何倍でしょうか？】

　往復の旅人算では、2人が「同じ場所から出発」するのか、「反対側から出発」するのか注意しなければなりません。特に「反対側から出発」する問題は、入試問題でも出題頻度が高い問題の1つです。１回目に出会うときと2回目に出会うときの進行図は覚えるまで練習してもいいと思います。次の問題で練習してみましょう。

　まず進行図をかいてみましょう。1回目に出会った地点をC地点とすると、図1のようになります。2回目に出会った地点をD地点とすると、図2のようになります。

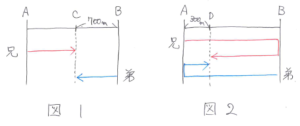
　ここで2つの進行図を見比べると、1回目に出会うまでの兄と弟が移動した道のりの和はAB間1本分で、2回目に出会うまでの兄と弟が移動した道のりの和はAB間3本分になっていることが分かります。つまり、出発してから2回目に出会うまでの時間は、出発してから1回目に出会うまでの時間の3倍になっているということです。
　弟の移動した道のりに注目すると、1回目に出会うまでにB→Cの700m移動しているので、2回目に出会うまでのB→A→Dの道のりは 700×3＝2100(m)と計算でき、このことからAB間の道のりは2100－300＝1800(m)と求まります。
　このように往復の旅人算は、出発してからN回目に出会うまでの時間は、出発してから1回目に出会うまでの時間の□倍になるという関係を利用すると解き易くなります。もちろん問題によって条件は異なりますから、まずは進行図に状況をかきこんで整理して考えることが大事になってきます。

【番外編　第11回から第14回の復習：素因数分解を使った約数の個数の数え方を覚えていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。

　・第11回　円すいの公式、回転体
　・第12回　道順、ぬり分け
　・第13回　倍数の見分け方、試合数
　・第14回　約数の個数、素因数分解の利用

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。