メールマガジン宝箱 Mail magazine

　今回の組分けテストは5年生、4年生ともに図形の問題での得点が偏差値アップにつながります！図形を見て、正解に至るための鍵となる部分に注目できているかどうか、チェックしておく必要があります。

　そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から5年生は第5位から第1位まで、4年生は第3位から第1位までのランキングにまとめました。メルマガを読んで、ぜひ偏差値アップ、クラスアップを実現してください！応援しています！

　さらに、このメルマガの5年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、偏差値アップ実現に大きく近づきます！頑張りましょう！
予想問題はこちらのページで無料公開します！

《5年　第6回組分けテスト》

【第5位　逆比の利用：A×X＝B×Yからすぐに逆比の関係を導けますか？】

　　比の文章題は問題文から比の関係を作り、それをもとに「比の１あたり」を求めていくという手順で考えていくと解き易いでしょう。

という問題を考えてみましょう。

　問題文を線分図に整理すると下のようになります。

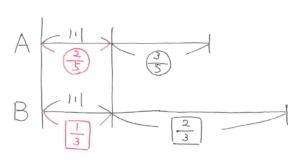
  このことから、A×2/5＝B×1/3とわかり、A：B＝5/2：3/1＝5：６となります。この比の差が10cmなので、マル1＝10cmとなります。

　したがって、Aの棒の長さは　10×5＝50(cm)となり、川の深さは　50×2/5＝20(cm)と求まります。

　A×X＝B×Yという関係式は分野を問わず出題されます。この関係式を見たらすぐにA：B＝1/X：1/Y　という逆数の比(逆比)を作り、A：Bを求めるのが問題を解く手筋になります。繰り返し練習して確実に身につけておきましょう。

【第4位　相似の利用：ピラミッド型やクロス型を見つける目を養いましょう！】

　平面図形の応用問題では「ピラミッド型」や「クロス型」の相似をみつけて、その比を利用して問題を解いていきます。次の問題を使って図形の中から相似を見つける練習をしてみましょう。

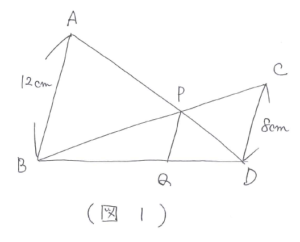
　という問題を考えてみましょう。

　この図の中には、3組の「ピラミッド型」や「クロス型」の相似があります。(図2)

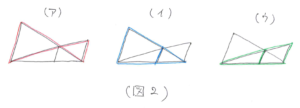
　問題の条件からどの相似の組を使うかを考えていきます。

　(図2)のアを使って、AP：PD＝12：8＝3：2となります。この比がわかったので、(図2)のイが使えるようになります。三角形ABDと三角形PQDの相似比は (3＋2)：2＝5：2となるので、PQ＝12×2/5＝4.8(cm)と求まります。

　相似を見つけられるかどうかは経験値に左右されます。多くの問題を解いて、見たことがある図形を増やすことが経験値を増やすことにつながっていきます。積極的に問題演習に取り組み、経験値を増やしていきましょう。

【第3位　比例式の利用：和一定でも差一定でもない時に比例式を使えていますか？】

　割合と比の文章題では「和が一定」でも「差が一定」でもない場合に、比例式を使って問題を解いていきます。比例式とは、A：B＝C：DのときにA×D＝B×C となる考え方です。

という問題を考えてみましょう。

　はじめの兄の所持金をマル7、弟の所持金をマル4とします。比例式を作ると

　(マル7－250)：(マル4－100)＝8：5

となります。式を整理して

　(マル7－250)×5＝(マル4－100)×8

　マル35－1250＝マル32－800

　これを線分図に整理すると下のようになります。

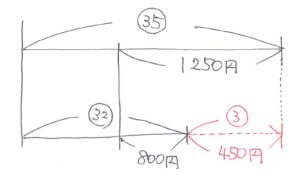
　この図から、マル3＝450、マル1＝150とわかります。したがって、はじめの弟の所持金は 150×4＝600(円)と求まります。

　比例式が利用できると、意外と簡単に解けてしまいます。実はこの方法は「和が一定」のときでも「差が一定」のときでも使うことができます。計算力に自信があるお子さんは、問題文からそのまま比例式を作れればあとは計算するだけなので、かなり早く解くことができます。ぜひ練習して身につけましょう。

【第2位　高さの等しい図形：同じ高さを正確に見つけられていますか？】

　「高さが等しい三角形の面積の比は、底辺の比に等しい」という重要な考え方があります。慣れるまではどこに高さが等しい三角形があるのかを見つけるのに苦労すると思います。次の問題を使って、図形の中から高さが等しい三角形を見つけて利用する練習をしてみましょう。

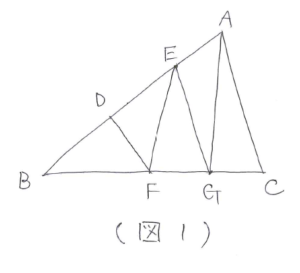
　BF：FG：GCから考えていきます。

　はじめに、BFが辺として使われている三角形を探すと三角形DBFと三角形EBFが見つかります。次にFGを辺として使っている三角形を探すと三角形EFGが見つかります。辺BCの側を底辺にしたときに、三角形EBFと三角形EFGは高さが等しいので、BF：FG＝2：1となります。(図2)

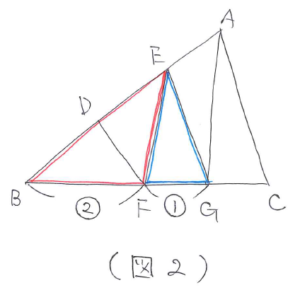
　今度はGCが辺として使われている三角形を探します。すると三角形AGCが見つかります。辺BCの側を底辺にしたときに三角形AGCと高さが等しい三角形を探すと、三角形ABGが見つかります。このことから(図3)のように、BG：GC＝4：1となります。

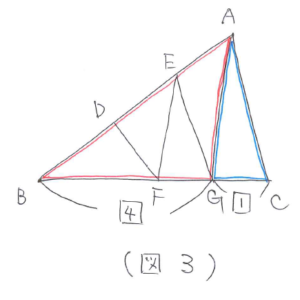
　(図2)と(図3)から同じBGの長さであることから、最小公倍数を使って比をそろえると(図4)のように、BF：FG：GC＝8：4：3と求まります。

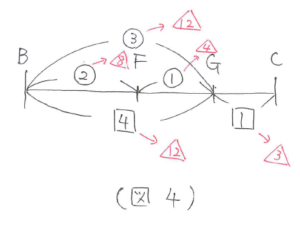
　AE：ED：DBも同じように考えていきます。

　AEが辺として使われている三角形を探すと三角形GAEが見つかり、辺ABの側を底辺にして三角形GAEと高さが等しい三角形を探すと三角形GEBが見つかります。このことから、AE：EB＝1：3となります。

　また、DBが辺として使われている三角形を探すと三角形FDBが見つかり、辺ACの側を底辺にして三角形FDBと高さが等しい三角形を探すと三角形FEDが見つかります。このことから、ED：DB＝1：1となります。

　EBの長さに注目して比をそろえると、BD：DE：EA＝3：3：2(図5)となるので、AE：ED：DB＝2：3：3と求まります。

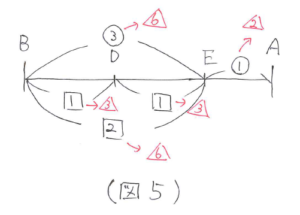
　この問題で目立つ間違いは、高さが等しくない三角形を使って比を作ってしまうというものです。目についた三角形をそのまま使うのではなく、高さが等しいか確認してから使っていきましょう。少しの注意でミスをかなり減らすことができます。

【第1位　比の積・比の商：比のわり算の式を正しく作れていますか？】

　次の問題を考えてみましょう。

　この問題でよくある間違いは、100円玉と50円玉の枚数の比を (100÷3)：(50÷2)＝4：3としてしまう間違いです。数字の意味を考えると「1枚あたりの金額÷金額」となり意味のない式になっています。これはお子さんの経験上、文章題では大きな数を小さい数で割ることが多かったため、数字の意味を考えずに計算してこのような間違いになっていると考えられます。このような勘違いを直すために、

とお子さんに伝えてみてはいかがでしょうか。例に挙げる金額は極端に大きな数にして、「見た目は小さな数でも、もともとは大きな数だったはず」という印象を付けられると今後間違いが減っていくでしょう。

　では問題を解いていきます。「枚数＝金額÷1枚あたりの金額」なので、100円玉と50円玉の枚数の比は (3÷100)：(2÷50)＝3：4 となり、100円玉は 28÷(3＋4)×3＝12(枚)、50円玉は 28－12＝16(枚)と求まります。したがって、お財布には入っていた金額は 100×12＋50×16＝2000(円)と求まります。

　比の積、比の商の考え方は、文章題だけではなく図形などでも使っていきます。しっかり練習していつでも使えるようにしておきましょう。

《4年　第6回組分けテスト》

【第3位　約数と公約数：余りは商より大きくならないことに要注意です！】

　0でない2つの整数A、Bがあり、AがBで割り切れるとき、BはAの約数になります。このことから約数の問題は「割り切れる」ところに着目して考えるとよいでしょう。

という問題を考えてみましょう。

　この問題のポイントは「割られる数から余りを引けばNで割り切れる」ということです。割り切れるという事から約数ですが、条件が2つあるので公約数を考えます。96－6＝90、58－4＝54なので、90と54の公約数を求めます。「公約数は最大公約数の約数」ですから連除法を使って最大公約数を求めます。最大公約数は18と求まるので、公約数は18の約数である｛1、2、3、6、9、18｝となります。ただし、Nは余りより大きい数です。したがって｛9、18｝のうち最も小さい9が答えとなります。

　公約数に気をとられて、余りの条件を見落とすミスが多いです。落ち着いて問題文の条件に当てはまるものを答えましょう。

【第2位　円と正多角形：正多角形の1つの内角の大きさを覚えてしまいましょう！】

　正多角形の問題では辺の長さが同じであることから、二等辺三角形を発見して考えることが多いです。問題文を読みながら、同じ長さのところに印をつけていくと発見しやすくなります。

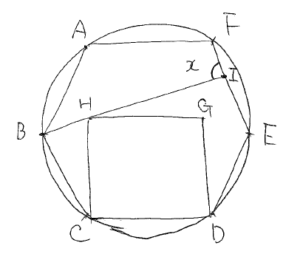
という問題を考えてみましょう。

　円を利用して正六角形の１つの内角を求めます。中心と各頂点を結ぶと、1つの二等辺三角形の中心の角度が360÷6＝60(度)となり正三角形だったとわかります。したがって正六角形の1つの角度は60×2＝120(度)と計算できます。

　正方形の1つの内角は90度なので角BCH＝120－90＝30(度)となります。また、正六角形と正方形は辺CDを共有しているのですべての辺の長さが等しくなっています。このことから三角形CBHが二等辺三角形とわかり、角CBH＝(180－30)÷2＝75(度)となります。

　ここで辺BCと辺EFは平行なので錯角が等しくなり、角CBH＝角BIF＝75(度)と求まります。

　正多角形の1つの内角は頻繁に使うのでこれを機に覚えてしまうとよいでしょう。ちなみに正三角形は60度、正方形は90度、正五角形は108度、正六角形は120度です。

【第1位　倍数と公倍数：2けたの2の倍数を求める割り算を正確にできていますか？】　

という問題を考えてみましょう。

　はじめに、2けたの整数の個数を求めると99－10＋1＝90(個)となります。

　次に、2けたの2の倍数の個数を求めます。99÷2＝49あまり1、9÷2＝4あまり1、49－4＝45(個)となります。このとき、2けたの整数の個数90個を2で割って 90÷2＝45と求めないようにしましょう。同じ数字なのであっているように見えますが、別の数の場合はずれてしまうことがあります。

　今度は2けたの7の倍数の個数を求めます。99÷7＝14あまり1、9÷7＝1あまり2、14－1＝13(個)となります。このとき、2けたの整数の個数90個を7で割って求めると、90÷7＝12あまり6となってしまい個数がずれてしまいます。こうしたずれが起きないように正しい解き方で求めましょう。

　また、2けたの14(2と7の最小公倍数)の倍数の個数は 99÷14＝7あまり1、1けたの14の倍数はないので7個と求まります。

　以上より、2けたの2の倍数または7の倍数の個数は 45＋13－7＝51(個)となり、2の倍数でも7の倍数でもない数は 90－51＝39(個)と求まります。

　このように、式の意味を考えないと間違えてしまうことがあります。気をつけて解いていきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。