メールマガジン宝箱 Mail magazine

　5年生の皆さん、11月のマンスリーは相似、そして流水算・通過算と、自分で手を動かして問題内容を整理できれば得点差を大きくつけることができる単元からの出題が多く含まれるテストです。クラスアップ実現のために、問題の内容に応じた自分だけの復習ポイントを正確に見出しておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　直角三角形の相似：相似の関係を把握するためには同じ角度に印をつけてみましょう！】

　相似の問題で、例えばピラミッド型や砂時計型であれば、どの図形が相似の関係にあるのかを正確に求められるお子さんでも、直角三角形の中に別の直角三角形が含まれるかたちになると、相似の関係を見つけづらくなってしまうことがあります。
　その要因として、図形の向きが変わってしまうだけで、視覚的に相似の関係の把握が難しくなることが挙げられます。

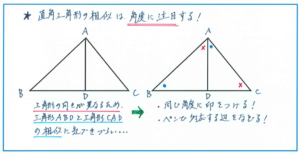
　典型的なピラミッド型や砂時計型は、平行線が見られることで、同位角や錯角がスムーズに見つけられるのですが、上の図のようなかたちになると、どの角度が同じになるのか迷ってしまいがちです。
　まずは右の図のように、同じ角度に印をつけてみると図形の向きが変わっていることへの意識を持ちやすくなります。そのうえで、ペンで三角形の枠をなぞりながら、「Ａ→Ｂ→Ｄと、Ｃ→Ａ→Ｄ」と口に出して対応する頂点を追ってみるとよいでしょう。
　慣れてくれば、視点を切り替えて相似の関係に気づくことができます。5年生のうちに、この直角三角形の相似を苦手と思ってしまわないように、地道な作業を重ねてみましょう。

【第4位　長方形内の相似：いくつかの相似の関係を的確に見つけられていますか？】

　長方形や平行四辺形の中に、対角線を含めた複数の直線が書き込まれた図形の中には、相似の関係が複数含まれることが多くあります。テストでも中盤の大問で出題されることが多く、こうしたタイプの問題を速く正解に行き着くことが、テスト全体の偏差値アップにつながります。
　こうした問題に対した際に、慣れない段階で頭の中だけで解こうとすると相似の関係を見つけづらくなってしまいます。
　そこで、下の図のように2つの長方形をかいて、それぞれに直線を書き込んでみると、それぞれの相似の関係を見出すことができます。

　このタイプの問題も第5位と同じく、慣れてくると問題を見てすぐに複数の相似の関係をつかむことができます。それまでは少し時間がかかっても自分で四角形をかいてみると、砂時計型の三角形を見る目が養われます。

【第3位　通過算：トンネルの長さが変わった時には迷わず状況図を！】

　通過算の問題では、状況図をかいて内容を整理すると一気に解きやすくなりますが、トンネルや鉄橋などの長さが変化するケースでは、状況図が断然の効果を発揮します。
　例えば次のような問題です。

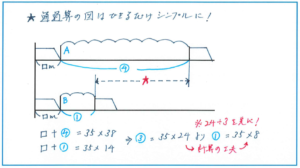
　上記のように状況図にまとめると、★の部分がトンネルBの長さの3倍にあたることが瞬時にわかります。あとは単位換算に注意して計算を進めるだけです。
列車の速さ→126÷3.6（×1000÷60÷60）＝35（m/秒）
★の部分の長さ→35×38－35×14＝35×(38－14)＝35×24（m）
①の長さ（トンネルＡの長さ）→35×24÷(4－1)＝35×8＝280（m）
列車の長さ→35×14－280＝210（m）
と正解に行き着くことができます。
　図をかく際のポイントですが、列車やトンネルを上記のようなシンプルなかたちにすることです。テストでは時間が限られますので、ポイントがわかる範囲で、図は簡単にかく練習をしておきましょう。

【第2位　流水算：変化する量に注意して問題内容を図にまとめられていますか？】

　流水算では様々な値が変化する問題に対応しなければなりません。図のかき方が身についていれば、そうした問題にもスムーズに解き進めることができます。
　例えば次のような静水時の速さ（船そのものの速さ）が変化する問題です。

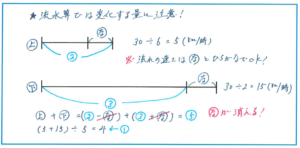
　まず図をかく前に、問題文からわかる数値を算出しておきましょう。
上りの速さ→30÷6＝5（㎞/時）
下りの速さ→30÷2＝15（㎞/時）
　この速さの関係が上の図のようにまとめられます。
　ここからは式の立て方がポイントになります。上りの際の静水時の速さを②、下りの際の静水時の速さを③とすると、以下のように式が立てられます。
　上りの速さ→②－（流れの速さ）＝5
　下りの速さ→③＋（流れの速さ）＝15
　ここで2つの式の（流れの速さ）の前が足し算と引き算になっていることに注目して、2つの式をそのまま足し合わせます。
　②－（流れの速さ）＋③＋（流れの速さ）＝②＋③＝5＋15＝20
　⑤＝20より、①＝4
　4×2－（流れの速さ）＝5より、川の流れの速さが時速3㎞と求めることができます。
　このタイプの問題に慣れてくれば、図をかかなくても式を立てることができますので、それまでは図をかいて問題内容を正確に整理するようにしましょう。

【第1位　流水算：速さの種類が多くなった際に、図を正確にかけていますか？】

　流水算の問題には、上りの速さ、下りの速さ、流れの速さ、静水時の速さと様々な種類の速さが出てきます。それらの関係を把握するためには図を正確にかくことが求められます。また、2つの船が向かい合って進む場合にはイメージをつかむためにも図が有効になります。
　次のような問題を例にして解法を考えてみましょう。

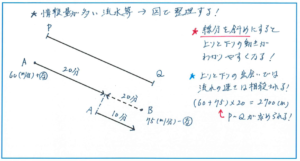
　流水算で2つの船が向かい合って進むパターンの問題では、上のように斜めの線分をかくことで、船の上りと下りの動きがよりわかりやすくなります。
　ポイントとなるのは、上りの船と下りの船が向かい合って進んだ速さの和では、流れの速さが消去されるため、静水時の速さの和になることです。
　船Ａが下る速さ→60（m/分）＋流れの速さ
　船Ｂが上る速さ→75（m/分）－流れの速さ
旅人算の考え方で2つの船の速さを足し合わせると、
　（60＋流れの速さ）＋（75－流れの速さ）＝135（m/分）

次に2つの船が出発して20分後にすれ違っていることから、川の長さが求められます。
　135×20＝2700（m）
ここで図から船Ａの動きに注目します。船ＡはＰ地を出発してから船Ｂとすれ違うまでが20分、それから10分後にＱ地に着きますので、20＋10＝30（分）かけてＰ地からＱ地に進んでいることがわかります。
2700mを30分かけて進んだことから船Ａの下りの速さが、
　2700÷30＝90（m/分）とわかります。
静水時の速さが毎分60mであることから、川の流れの速さが、
　90－60＝30（m/分）と求められます。

　問題文に出てくる速さの種類が増えてきた場合、頭の中だけで解こうとすると、解答の方針がうまく立てられなくなってしまいがちです。そこで図で問題内容を整理できれば、解答への道筋が立てられ、スムーズに式を立てることができます。情報量が多い場合には図が効果的となるタイプのひとつの問題です。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。