メールマガジン宝箱 Mail magazine

　平面図形の相似、速さの比といった入試でも頻出の単元の演習が進み、テスト問題でも比を使いこなす必要がある問題が一気に増えてきます。問題文を正確に読み取って、比を活用する練習を重ねておきたいところです。
　そこで、12/5（土）の実力判定テストの対策ポイントをプロ家庭教師の視点から5つのポイントにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日11/27（金）公開の予想問題と連動していますので、予想問題も合わせてご利用ください！
予想問題はこちらのページで無料公開します！

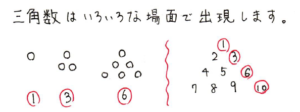
【直前チェックポイント第5位：三角数は和を分解して攻略することが秘訣です！】

　次のような問題には、どのように対応すればよいでしょうか。

　頻出の問題ですが、この数列では不用意に差に着目すると正解が遠のいてしまいます。次のような発想を持つとあざやかに解くことができます。
　1＝1
　3＝1＋2
　6＝1＋2＋3
　10＝1＋2＋3＋4
　15＝1＋2＋3＋4＋5
　和に分解するという発想です。これに気づくと、答えはもう簡単です。
　10番目の数は、1＋2＋3＋4＋5＋6＋7＋8＋9＋10＝55です。
　このような数の並び方を三角数といいます。三角数は、ご石を正三角形型に並べていくときにも表れます。場合の数にも登場したりと、いろいろな場面で本当によく登場しますので、1,3,6,10という並び順に気づいたら、差を取らず、和分解して解いていきましょう。

【直前チェックポイント第4位：速さの単位換算を解く秘訣は自信と要領です！】

　単位換算はできて当たり前という前提で入試問題が作られますが、実際は苦手としているお子さんがとても多いです。意外に多いのは、仕組みは理解しているのだけれど計算値があまりにも微妙で不安になってしまい、正しい計算とは逆の方法をとってしまうという場合です。
　以下の問題でスムーズを正解できているか、チェックしてみてください。

　答えはそれぞれ（分速）1000（m）、3600（分）、1（時間）34（分）、（分速）2（m ）です。
　(1)、(2)について。時速→分速のときは÷60をするのに、時間→分では×60をします。似たような言葉の変換作業でありながら、60をかけたりわったりするので、混乱しがちです。(1)、(2)を同時に出されると混乱してしまうかもしれません。
　しかも、(2)は60×60をしたら答えが大きすぎるのに対し、60÷60をしたらきりがよいので、数字の妥当性を追求した結果、直感に頼って、つい÷60をしてしまう、ということがあえます。
　(3)ですが、テキストでも割り算をメインに解説しているので、つい小数で計算しがちです。しかし、速さの問題では3の倍数が多用されるので、割り切れないことがかなり多いです。割り切れなかったら小数計算に早々と見切りをつけ、分数計算でやりなおすようにしましょう。
　(4)はどうでしょうか。0.12÷60をしようとすると、答えがあまりにも小さすぎて不安になり、直感で0.12×60とやってしまう可能性があります。先に0.12×1000＝120mと単位を換えてから120÷60＝2と計算すれば、つまづかなかないでしょう。

　このように、単位換算はいくら仕組みが理解できても、それが実践できなかったり、要領のよい計算方法を取らないとなかなか正解にたどり着きません。ある程度仕組みが理解できたら、正解できるかどうか、ちょっと不安になるような問題を中心に練習を重ねると効果的です。
　(2)が不安な場合は、テスト前に、第11回本科のオプション理解をこなしたあと、「考えよう1」、「考えよう2」に取り組みましょう。
　(3)、(4)が不安な場合は、テスト前に、第11回本科のオプション活用に取り組んでみてください。

【直前チェックポイント第3位：平均の速さの問題は、定義の確認と情報の整理が正解するための秘訣です！】

　次のような問題で、正しく式が立てられていますでしょうか。

　行きと帰りの速さを足して2で割ったものを平均の速さとは言いません！　直感に反するため、ここでつまづく人が多数います。本科テキストや栄冠、授業のノートを見返してみてください。平均の速さとは、「進んだ道のりの合計」を「かかった時間の合計」で割ったものをいいます。
　ところで、速さの問題が難しいのは、扱う情報があまりにも多いからです。この問題に限っても、行き、帰り、往復、それぞれに道のり・速さ・時間が関わります。なんと、9つもの情報を取り扱わなくてはいけません。
　扱う情報が多い場合は、表に整理してから解くとわかりやすくなります。
　

　このように、速さの問題は、道のり・速さ・時間の関係を表に整理すると理解しやすいです。実際、中高一貫校向けの中学校の数学の教科書でも表を使って整理しており、速さの問題の情報の整理術として今後も使える手法です。

　ちなみに、道のりがわかっていなくても平均の速さを出せます。

　こちらも表に整理してみたいと思いますが、問1と比べると、道のりも時間もわかっていません。圧倒的に情報が少ない場合は、十中八九、比の出番です。
道のりが同じ場合は時間と速さは逆比の関係だということを思い出してください。

【直前チェックポイント第2位：相似の三角形＋高さが同じ三角形の融合問題に慣れましょう！】

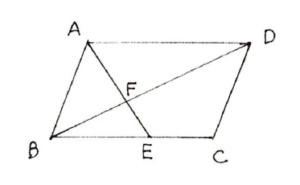
　相似単独の問題だと解けるが、ちょっとでも他の図形が組み合わさると解けなくなる…。そんなお子さんの最初の関門となるような問題です。相似な三角形と、高さが同じで底辺が違う三角形とが融合する問題に、誘導なしで答えられるようになっておきましょう。
ポイントは2つあります。

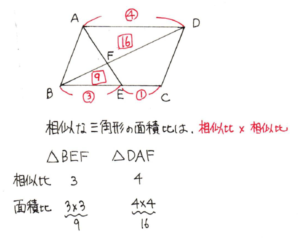
　BE:AD＝3:4なので、三角形BEFと三角形DAFの面積比は9:16になります。相似比と面積比の関係がすぐに出てこない場合は、第10回栄冠のチェックポイント4をおさらいしておきましょう。

　三角形BEFと三角形DAFの底辺であるBE:ADが3:4なので、側辺であるEF:FAも3:4です。ここが鍵です。側辺に視点を変更できるかが攻略の鍵です。
　EF:FA＝3:4ということに気づけば、三角形BEFと三角形ABFの面積比も3:4だということに気づけます。

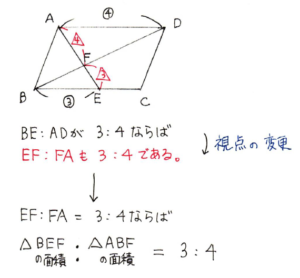
　よって、三角形BEFと三角形DAFと三角形ABFの面積比は以下のようになります。

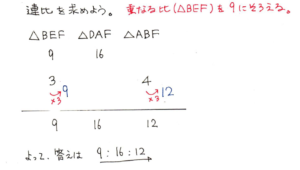
　3つの比、すなわち連比の場合は、2つずつに分けるのがコツでしたね。不安な場合は栄冠第6回のチェックポイント1をおさらいしておきましょう。

【直前チェックポイント第1位：同じ方向に2人が進む進行グラフの2つのパターンをおさえておきましょう！】

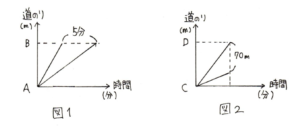
　どちらの進行グラフも三角形ができるのがわかると思います。図1は底辺が時間軸に対して水平の三角形で、図2は、底辺が時間軸に対して垂直の三角形です。
　進行グラフの着眼点はいろいろあるのですが、今回は次のことを覚えましょう。

　比の関係を整理し、2人の差に着目できれば、あとは答えまで一直線です。

　進行グラフが関わる問題は、2つの形態の三角形どちらかに着目して、比の関係に持ち込めば、正解が近づきます。実戦で試したい場合は、予想問題大問6の(1)に取り組んでみてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。