メールマガジン宝箱 Mail magazine

　新5年生の皆さん、1月の組分けでは図形問題、後半の思考力を求める問題で確実に得点を重ねることが偏差値アップにつながります。図形問題では同じ長さや面積を確実に見つける目を、思考力問題では書き出しなどを行い問題文の条件を正しく整理する力を着実に鍛えておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【直前チェックポイント第5位：半径のわからない円の面積の求め方をマスターしましょう！】

　次のような円の半径が分かっていない問題には、どのように対応すればよいでしょうか。

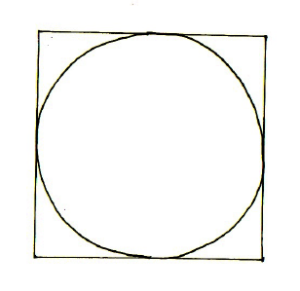
円の半径が求められなくても、半径×半径の値なら求められることがあります。半径×半径の値を求める方法をおさらいしておきましょう。ポイントは正方形を4分割することです。

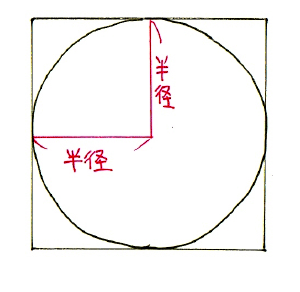
　4分割した正方形の1辺は、4分割した正方形の面積と半径×半径の値は一致します。
　つまり、半径×半径＝40÷4＝10
　よって、円の面積は、10×3.14＝31.4平方cmです。

　次のような問題はどうでしょうか。

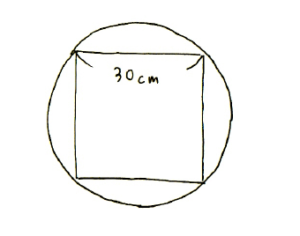
　この問題も正方形を4分割してみましょう。ポイントは対角線で4分割することです。

　直角二等辺三角形の直角をはさんだ2辺（□の部分）がちょうど円の半径です。
　つまり、□×□＝半径×半径です。
　直角二等辺三角形の面積を使って、□×□を逆算で求めましょう。直角二等辺三角形の面積は、正方形の4分の1ですから、30×30÷4＝225平方cmです。
　したがって、
　□×□÷2＝225
　□×□＝450
　よって、半径×半径＝450より、円の面積は、450×3.14＝1413平方cmと求められます。

【直前チェックポイント第4位：2つの部分の面積の和や差を正確に求められていますか？】

　2つに分かれた部分の面積の和や差を求める際に、それぞれの部分の面積を求めるよりも速く正確に解ける方法があります。
　

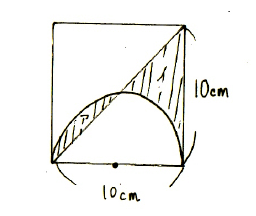
　アとイそれぞれを、単独に求めて足すこともできなくはないですが、無駄が多くなります。面積の和を求める場合は、どちらかを移動させて、一気に求めてしまいましょう。

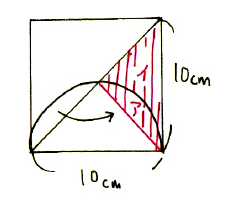
　アとイの面積の和は、おうぎ形から直角三角形を引いたものになります。10×10÷4＝25平方cmです。円周率なんて1回も使いませんでしたね。

　次のような問題でも、解き方をよく考えてから臨みましょう。

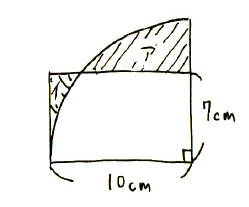
　差を求める場合は、共通になりそうな部分「ウ」をあえて加えて考えます。
　ア－イとは、（アウ－イウ）でもあります。

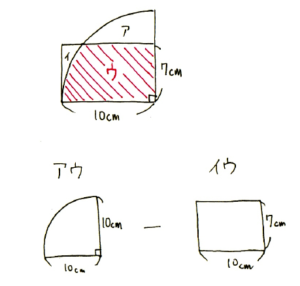
　アウ、イウはそれぞれ求めやすいですね。
　アウ：10×10×3.14×1/4＝78.5（平方cm）
　イウ：10×7＝70（平方cm）より、
　アウ－イウ＝78.5－70＝8.5（平方cm）
と求められます。

【直前チェックポイント第3位：場合の数で、ぬりわけ問題で数え方の工夫ができていますか？】

　場合の数の問題の中でも、ぬりわけ問題は解き方の工夫ができるかどうかで、得点力に大きく差がつく問題です。

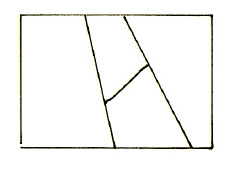
　この問題、4つのエリアに名前がついていません。エリアが名無しのままだと、何かと不便です。4つのエリアに、ア、イ、ウ、エと記号をふってしまうと、一気に解きやすくなります。
　正確に数えることは、算数で問われる基本的な能力の一つです。数えるなんて簡単かと思われるかもしれませんが、名前のないものを数えろと言われても大変苦労します。場合の数では、数えるために工夫して整理できるかが問われていると思ってください。
　
　図のように、エリアに記号をふります。

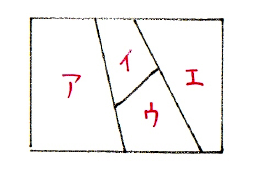
　アから順番に色を決めていきます。
　アは、どの色も使えるので、4通り。
　イは、アで使った色以外を使えるので、3通り。
　ウは、アとイで使った色以外を使えるので、2通り。
　エは、イとウで使った色以外を使えるので、2通り。
　よって、4×3×2×2＝48通りです。

　さらに次のような問題にも取り組んでみましょう。

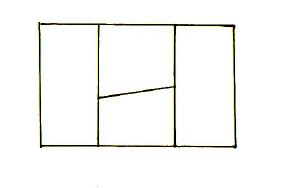
　エリアの数より使う色の数が少ないときは、樹形図を書いて考えるとよいでしょう。
　この問題も、まずは4つのエリアに、ア、イ、ウ、エと記号をふってしまいます。また、それぞれの色に番号をふって、漢字や頭文字（そもそも赤と青の頭文字はどちらも「あ」なので、困った経験があるかもしれません）の代わりに番号で樹形図を書くと、書くわずらわしさも減り、大小関係や順番もわかりやすくなり、頭の中もスッキリします。

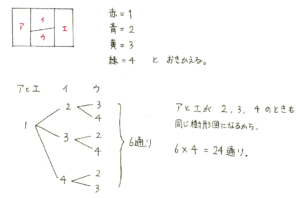
　数え方の工夫や樹形図の活用といった解き方を身につけておけば、場合の数も得点源にできるのです。

【直前チェックポイント第2位：グループ分けする数列で、線を活用できていますか？】

　数列の問題の中で、グループ分けが必要なタイプがあります。

　次のようにグループ分けして考えます。

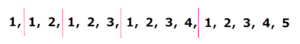
　1から10まで足すと、55になることは覚えておきましょう。
　そうすると、55番目が10グループ目の最後ですから、60番目は、11グループに突入して、5つ進んだ数です。1，2，3，4，5より、答えは5です。
　グループ分けする際は、グループを区別する線を入れると、ミスを防ぐことができます。

【直前チェックポイント第1位：倍数と約数の文章題で数の大小関係をイメージできていますか？】

　倍数と約数の問題はテストの前半で出されることが多いですが、それだけに確実に得点しておきたいところです。

　「16でわる数」とは、☆÷16の☆に当たる数です。イメージとしては、長い棒を16cm間隔でわっていくということです。
　「16をわる数」とは、16÷☆の☆に当たる数です。イメージとしては、16cmの棒を細かくわっていくということです。
　「で」と「を」では意味が違います。言葉に敏感になるようにしましょう。

　16でわって100にもっとも近い数は、100÷16＝6あまり4より、96です。これにあまりの2を足すと、98。これがいちばん100に近いので、答えは98になります。

　次のような問題の解き方も覚えられているでしょうか。

56をわると2あまり、75をわると3あまるような整数のうち、最小の数はいくつですか。

　また、あまりが2と3ですから、3より大きくないといけません。
　こうした数の大小関係を確実にイメージすることが失点を防ぐ大きなポイントになります。
　56をわると2あまる整数は、54の約数、75をわると3あまる整数は73の約数です。2つの最大公約数が18ですから、18の約数は、1、2、3、6、9、18です。このうち、3より大きい数は、6となります。

　いかがでしたでしょうか。中には「倍数、約数の問題であれば楽勝だ」と思った方もいらっしゃるかと思います。しかし、この時期のマンスリーや組分けテストでは、「基礎トレ」レベルの問題が過半数を占めます。　
　にもかかわらず、やったはずの問題、できていた問題を取りこぼすことで失点してしまうお子さんが多いのは、ひとえに基礎を簡単だと思ってしまうからです。何回もていねいに復習するお子さんは、そのたびに新しい発見をします。
1回できたからと安心するのではなく、定着するまで解き直すようにして、じっくり取り組んでください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。