メールマガジン宝箱 Mail magazine

　新6年生の皆さん、2月マンスリーは線分図を使って解く問題でどれだけ正解を重ねられるかが、偏差値アップのポイントです。
　速さと比の問題やニュートン算では、問題内容を正確に線分図でまとめることで、解法のイメージがつかみやすくなります。
問題を読んで、どのように線分図をかけばよいのかがすぐに判断できるように、図のかき方をしっかりと固めておきたいところです。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　食塩水の濃度：「濃さが等しくなる」場合の解き方を覚えていますか？】

　食塩水の濃度の中で、異なる濃度の食塩水を混ぜ合わせるタイプの問題はテストでも頻出です。ビーカー図を使って混ぜ合わせのやりとりを正しく把握することが大事ですが、まず気をつけて頂きたいのが、「混ぜ合わせた結果、濃さが等しくなるパターン」です。
　もとからある食塩水に、水も食塩も足さず、ただ互いにやりとりする場合には、「濃さが等しくなる」のは問題を解く上で大きなヒントになりますので、見逃さないようにしましょう。
例えば次のような問題です。

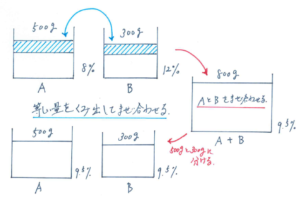
　食塩水の混ぜ合わせですので、面積図や天びん図を使って解くことにはなりますが、くみ出した食塩水の量がわからないので、すぐには図をかき始められないところです。
　そこで、等しい量の食塩水をやりとりしたことに注目してみましょう。Ａの容器の食塩水は500ｇ、Ｂの容器の食塩水は300ｇのままで変わらずに、食塩も水も新たに追加されていません。それで2つの容器の濃さが等しいので、上の図のような、大きなビーカーにＡ、Ｂそれぞれの食塩水を入れてよくかきまぜて、それをＡに500ｇ、Ｂに300ｇ戻したことと同じになります。
　大きなビーカーにある800ｇの食塩水の濃さは、それぞれの容器に含まれる食塩の量を出せば、図なしで求められますが、練習にもなるので、面積図（天びん図）で解いてみましょう。
　大きなビーカーにある800ｇの食塩水の濃さは9.5%になりますので、ここからは容器Ａのみに注目して、解き進めます。
　問題の内容が、「8%の濃さの食塩水と12%の濃さの食塩水を混ぜ合わせて9.5%の食塩水500ｇになりました。12%の濃さの食塩水は何ｇですか。」と変わったことになります。
　ここからは面積図・天びん図を使えば正解に行き着くことができます。500×3/8＝187.5より答えは187.5ｇとなります。
　濃さの混ぜ合わせは必ずビーカーでやりとりを示す、と決めつけず、まずは問題文中から活用できる内容を見つけ出しましょう。

【第4位　Ｎ進法：Ｎは一ケタの数だけとは限りません！】

　Ｎ進法の問題は、解き方に慣れてしまえば難しさは感じないのですが、逆に解き方を覚えていないと、手も足も出なくなってしまいます。特に、問題文を読んで、Ｎ進法を使って解くことに気づけるかどうかがポイントになります。Ｎ進法ならではの問題の表現に注意を払うように気をつけながら演習を進めましょう。
　また、Ｎ進法のＮの数字は必ずしも1けたとは限りません。次のような問題で、Ｎが2けたの数になっても基本的な解き方は変わらないことを確認しておきましょう。

　例えば5進法であれば、一番右の位が「1の位」、その右が「5の位」、その右が「5×5の位」…と数字が大きくなる構成になります。
　それが11進法になっても、位の取り方は同じです。一番右の位が「1の位」、その右が「11の位」、その右が「11×11の位」となりますので、問題の「234」は、11×11×2＋11×3＋1×4＝242＋33＋4＝400と求められます。
　Ｎの数が大きくなっても焦ることなく、基本的な解法をそのまま使って正解できれば、テストで得点差を生み出すことができますので、反復演習で解き方に慣れましょう。

【第3位　場合の数：問題内容に合わせた場合分けはできていますか？】

　場合の数の問題で「場合分け」が重要なことは、このメルマガでも何度かお伝えしてきました。問題を見て、どの部分に注目して場合分けをするのか、すぐに気がつくようになると、テストでも速く正確に解答に行き着くことができます。
　次のような問題で、場合分けの方法を考えてみましょう。

　ここでは、百の位に注目します。3ケタの数を作るにあたって、0は百の位に入ることができませんので、百の位にどの数が入るかによって場合分けをすると、解きやすくなります。
百の位が1の場合：（十の位、一の位）とすると、（02）（03）（20）（23）（30）（32）（33）→7通り
百の位が2の場合：（01）（03）（10）（13）（30）（31）（33）→7通り
百の位が3の場合は、計算で求めます。樹形図をかいてもよいですが、時間がかかってしまうので、計算で解く練習をしておきましょう。
十の位には0から3の4つの数字、一の位には十の位で使った1枚以外の3つの数字が入るので、4×3＝12（通り）になります。
よって、合計して7×2＋12＝26（通り）と求められます。
　あてはまる数を頭の中で浮かべるのではなく、すぐに書き出す習慣を身につけておきましょう。

【第2位　ニュートン算：線分図をかいて解く流れを確実に身につけましょう！】

　今回のマンスリーテストでは、線分図を使って解く問題をいかに多く正解するかが、偏差値アップのポイントになります。
　その代表例のひとつがニュートン算です。ニュートン算は出題のされ方がパターン化されていますので、問題を見てすぐにニュートン算であることがわかりやすいです。ニュートン算の問題かどうかの判断が少しでも曖昧な場合は、デイリーの復習を急ぎ進めてください。
　一方で、解き方がわからないと手も足も出ないのがニュートン算でもあります。典型的な問題を使って、線分図で内容を整理する解法をしっかり固めておきましょう。

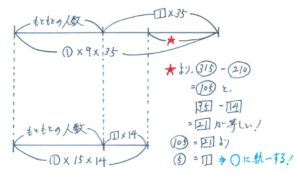
　線分図をかく流れについて整理しましょう。
　まず、上のように2本の線分図をかき、左端にもともとあった量（この問題では、開園前に行列にいた人数）を置きます。
　次に単位量あたりに減る量をマル1、増える量をシカク1とします。
　線分図の差からマル1とシカク1の関係を式にして、どちらかの記号に統一します。
　この流れで進めると、まず窓口を9か所開けた場合は、35分で入園する人数がマル315、15か所開けた場合は、14分で入園する人数がマル210となります。
　線分図の長さの差を、マルとシカクで表すことで、マル315－マル210＝シカク35－シカク14より、マル105＝シカク21からマル5＝シカク1となります。
　そこで記号をマルで統一すると、開園前に行列にいた人数がマル315－マル5×35＝マル140と表せることになります。
　最後に、25か所で1分間に入園できる人数がマル25、1分間に増える人数がマル5となることから、140÷(25－5)＝7より7分と答えが求められます。
　解き方の流れさえ確実に身につければ、テストで得点源にできる単元です。問題文がわかりづらい、と決めつけずにじっくり解法を身につけてください。

【第1位　速さの問題：線分図を使うと、逆比の関係が視覚化できます！】

　速さの問題の中でも線分図を使うと、解法が一気に見えてくる問題が多くあります。特に逆比を使って解く問題の場合には、線分図をかくことで「どの部分の逆比の関係になるのか」が、視覚的にもとらえやすくなり、正解できるチャンスが大きく広がります。
次の問題を例に考えてみましょう。

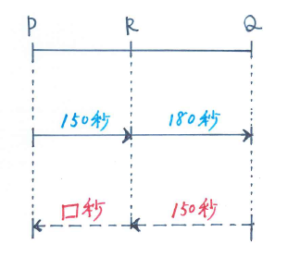
　問題を見た瞬間に「同じ道のりを進む場合に、速さと時間が逆比になる」というポイントはすぐに浮かんでくるでしょう。　　　　　　

　ただ、そこから頭の中だけで解こうとすると、思わぬところでミスをしてしまいます。丁寧にかき過ぎる必要はありませんので、まずは線分図で状況を整理してみましょう。

　上の図のように、Ｐ駅からＱ駅に向かう電車の動きを実線、Ｑ駅からＰ駅に向かう電車の動きを点線とします。このように少し手間がかかっても、それぞれの動きを表す線を別にした方が、ミスを大きく減らせます。
　電車がすれ違う場所をＲとおくと、同じＱとＲの区間を、実線の電車は（330－150＝）180秒で、点線の電車は150秒で進むことがわかり、ここから2つの電車の速さの比は1/180：1/150＝5：6と把握できます。　
　そこでシカクで表した、点線の電車がＲからＰに進む時間は、150×5/6＝125（秒）と求められます。
ここで答えを125秒＝2分5秒、としないように十分に気をつけてください。求めるのは、「発車してからＰ駅に着くまでの時間」ですので、150＋125＝275（秒）より、4分35秒となります。
　線分図を使って解くことで、最後に求めるものを間違わないという効果もあります。すべての問題で線分図を使う必要はありませんが、正確に答えに行き着くためには、線分図の効果がとても大きいことをしっかり意識しておいてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。