メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、6年生は面積比と底辺比の関係がわかるように図形にかき入れたり、規則性の周期をつかむための書き出しをするなど、手を動かして問題内容を把握すること、5年生は問題内容に合わせて線分図や面積図を正確に使いこなすことが偏差値アップのポイントになります！問題の条件を確実につかめているかどうかを、しっかりチェックしておきたいところです。
　そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から6年生、5年生ともには第5位から第1位までのランキングにまとめました。メルマガを読んで、ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このメルマガの6年生のランキングは明日3月5日（金）公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、偏差値アップのための万全の準備が整います！頑張りましょう！
予想問題はこちらのページで無料公開します！

6年第1回組分けテスト

【第5位　和と差に関する問題：ベン図を使って内容を整理できていますか？】

　文章題では条件を図や表などを使って整理すると、見通しが良くなることが多いです。代表的なものとして線分図や面積図、ベン図などがあります。また、その問題特有の図や表をかくこともあるので、ひとつひとつ確認して身につけていきましょう。

　(図1)をベン図にしてみます。

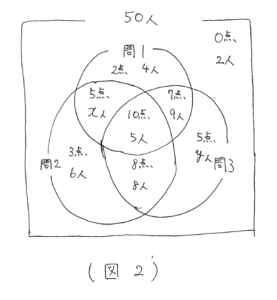
　このとき、5点の場所が2か所あることに注意してください。ここでは、問1と問2を正解した人をx人、問3だけ正解した人をy人としています。
　また、1問まちがいという条件を正確に使いましょう。問1だけをまちがえた人は、3＋5＝8(点)、問2だけをまちがえた人は、2＋5＝7(点)、問3だけまちがえた人は、2＋3＝5(点)になります。(図2)

　以上より、x＋9＋8＝28となり、x＝11(人)とわかります。5点の人は16人いますから、y＝16－11＝5(人)となり、問3を正解した生徒は、5＋8＋5＋9＝27(人)と求まります。
　3つのベン図は、今までに練習する機会が少なかったと思います。重なっている部分が何を表しているかに注意して練習しましょう。

【第4位　場合の数：問題内容に合わせて公式を使い分けられていますか？】

　場合の数では順列や組み合わせを求めるときに便利な公式があります。公式を使うためには前提となる条件が必要なので、公式が使える場面なのかしっかり考えることが重要です。

【第3位　N進法：問題を見てN進法の問題であると正確に判断できていますか？】

　N進法は2つの段階に分けて練習すると効果的です。1つ目の段階は、N進法の基本を理解して「N進法⇒10進法」、「10進法⇒N進法」の計算を迷わずにできるようにすることです。単純に「2進法の1011を10進法に直せ」、「10進法の75を3進法に直せ」といった計算を繰り返します。ちなみに前者の答えは「11」で後者の答えは「2210」です。
　2つ目の段階は問題で使われているN進法に気付いて、それを使い問題を解くことです。これは「何種類の数字を使っている」、「いくつのときに繰り上がっている」といったことから考えられます。次の問題を使って、2つ目の段階を練習してみましょう。

という問題を考えてみましょう。
　まず問題を見て、「4種類の数字を使っている」「4個集まると繰り上がる(3→10、13→20で確認できる)」ことから、4進法であることがわかります。
　4進法は一番右の位が「1の位」で、1が4個集まると繰り上がることから右から2番目の位は「4の位」になります。同様に、4が4個集まると繰り上がることから右から3番目の位は「16の位」、16が4個集まると繰り上がることから右から4番目の位は「64の位」となっています。したがって、4進法の2021を10進法に直すと 64×2＋16×0＋4×2＋1×1＝137 となるので、137番目と求まります。
　次に150番目の数を求めます。これは「10進法の150を4進法で表すといくつか。」と同じ意味です。4進法ですから4個ずつの組を作って考えます。
　 150÷4＝37…2　 ← 4(1を4個組にした)が37個できて1が2個余っている
　 37÷4＝9 …１ ← 16(4を４個組にした)が9個できて4が1個余っている
9÷4＝2 …1 ← 64(16を4個組にした)が2個できて16が1個余っている
以上の事から、、2112と求まります。
　このように問題を読んだ時の着眼点がわかってくるとN進法に気付きやすくなります。いろいろな問題で試してみてください。

【第2位　平面図形：面積比と底辺の長さの比の関係を正確に使えていますか？】

　予習シリーズ5年下の第3回で学習した「高さが等しい三角形の面積の比は、底辺の長さの比と等しい(図1)」を少し応用すると(図2)の関係が成り立ちます。
　　

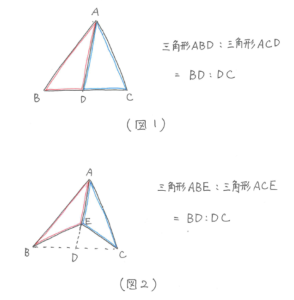
　これを使って、次の問題を考えてみましょう。

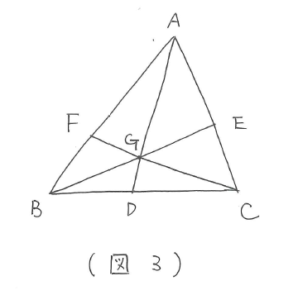
　(図2)の公式から
　BD：DC＝4：5　なので、三角形ABG：三角形ACG＝4：5
　AE：EC＝3：2　なので、三角形ABG：三角形BCG＝3：2
とわかります。ここで連比を作ると、
　三角形ABG：三角形BCG：三角形CAG＝12：8：15
となります。(図4)
　

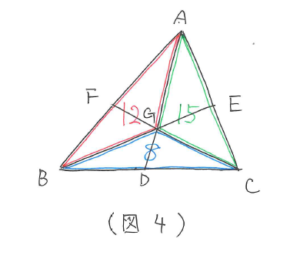
ここで再び(図2)の公式を使うと、AF：FB＝15：8　と求まります。
　平面図形の問題はいろいろな解き方ができることが多いです。問題によっては普段自分が使っている解き方では解き難い問題もあります。そのため、いくつかの解き方を用意して問題によって使い分けられると、対応できる問題が増えておすすめです。少しずつ解き方を増やしていきましょう。

【第1位　規則性：どのような周期かを知るには書き出しが抜群の効果を発揮します！】

　規則性の問題では、計算して出た答えが何を表しているのかを考えながら問題を解くこと(例えば植木算で、「木の本数」なのか「間の数」なのか等)が特に重要です。処理が長くなる問題では途中で混乱しないように気をつけましょう。

という問題を考えてみましょう。
　3と5の最小公倍数は15なので、これを利用してまとめると、(図1)のようになります。

　これは、15で割ったときの余りが同じになる数がたてに並んでいます。余りは｛1、2、4、7、8、11、13、14｝の8個の周期になっています。よって、77÷15＝5あまり2　となるので、8×5＋2＝42(番目)と求まります。
　また、100番目の数は、100÷8＝12あまり4　→　周期の4番目　→あまりが7の列　となるので、15×12＋7＝187　と求まります。
　混乱しないために単位をかきながら計算したり、何を求めているか言葉を残したりすると効果的です。見直しにも使えるので余裕があればかいてみるといいでしょう。

5年第1回組分けテスト

【第5位　割合の基本：公式はまず問題をしっかり読んでから使うようにしましょう！】

　割合はしっかり文章を読んで、「割合」「もとにする量」「くらべる量」を探し出すことができれば難しくありません。しっかり見つけられるようになるまで練習をしていきましょう。
　まずは短い問題から。

　この問題ではすぐに600円と分かりますが、じっくり文章を見ていきます。
　最初に注目するのは「割合」です。「割合」を表す言葉は「△倍」や「A/B」など文章の中から見つけ易いです。この問題では「2倍」です。
　次に探すのは「もとにする量」です。先ほど見つけた「割合」の前に「の」という助詞が入っています。その「の」の前が「もとにする量」になります。
　ここまで考えて式を立てます。「くらべる量＝もとにする量×割合」なので、300×2＝600
となります。しっかり考えるとこうなりますが、実は簡便的なやり方もあります。それは問題文の「もとにする量」と「割合」の間にある「の」を「×」に置き換えると式が出来てしまうというやり方です。
他の問題でも試してみましょう。

　順番に考えていきます。「割合」は「1/5」です。その前に「の」があり、さらにその前の「お母さんの年令」が「もとにする量」になります。したがって、「の」を「×」に置き換
えて式と立てると、30×1/5＝6(才)となります。
　もう1題やってみます。

　まず「割合」は「1/10」です。その前に「の」があり、さらにその前の「クラス全体」が「もとにする量」になります。したがって、「の」を「×」に置き換えて式を立てます。クラス全体の人数を□とすると、□×1/10＝3という式が立てられます。逆算をして、□＝3÷1/10＝30(人)と求まります。
　あくまでも簡便的なやり方なのですべての問題で使えるわけではないですが、基本的な問題では威力を発揮します。ぜひほかの問題でも試してみてください。

【第4位　図形の面積：30度、60度、90度の直角三角形を活用できていますか？】

　3つの角の大きさが、30度、60度、90度の直角三角形(三角定規)は、2つ組み合わせると正三角形になることから、斜辺の長さは1番短い辺の長さの2倍になっています。このことを考えて次の問題で練習してみましょう。

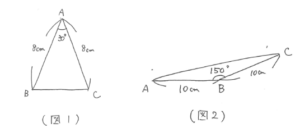
　(図1)は補助線を引くと(図3)のようになります。よって面積は、8×4÷2＝16(平方cm)と求まります。

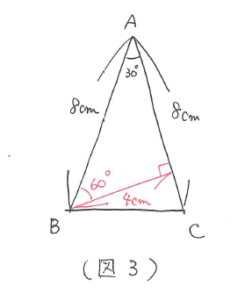
　(図2)は補助線を引くと(図4)のようになります。よって面積は、10×5÷2＝25(平方cm)と求まります。

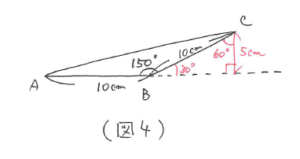
　図形の中に、この三角定規の形が隠れています。いろいろな問題に触れて、見つけられるようになりましょう。

【第3位　約数・倍数：解く「順番」に気をつけると時短で解き進められます！】

　約数・倍数の問題では、問題文にある数字を組み合わせても答えは出ません。順序良く考える練習をしながら、少しずつ量の多い問題が解けるようにしていきましょう。

という問題を考えてみましょう。
　まず「5で割ると3余る数」を書き出します。このとき、一番小さい数が3であることに注意しましょう。(3÷5＝0あまり3)
　3、8、13、18、23、28
　このとき、5と6の最小公倍数である30までの数で考えます。
　続いて「6で割ると5余る数」を書き出します。こちらは同じ数が出るまで書けばいいでしょう。もちろん一番小さい数は5です。(5÷6＝0あまり5)
　5、11、17、23
　調べた結果、23が「5で割ると3余り、6で割ると5余る数」の中で一番小さい数だとわかります。あとは、23から5と6の最小公倍数の30ずつ数が増えていくので等差数列になっています。
　23、53、83、……
　したがって、小さい方から5番目の数は 23＋30×(5－1)＝143 と求まります。
　次に400に一番近い数を求めます。逆算の式をたてて、23＋30×(□－1)＝400 として計算してみます。□＝(400－23)÷30＝12.5… となるので、等差数列の12番目辺りだと見当をつけて調べます。 23＋30×(12－1)＝353、353＋30＝383、383＋30＝413 となり、400に一番近い数は413と求まります。
　書き出したり、調べたりする時間は練習すれば減らすことができます。解き方が決まっている問題で悩まないように、しっかりと考え方を身につけましょう。

【第2位　割合の応用：もとにする量が変わる問題で線分図を使いこなせていますか？】

　もとにする量が途中で変わる問題では、文章をよく読み何をもとにしているのか間違えないようにしましょう。ポイントはやはり「割合」の前の「の」のさらに前が「もとにする量」になるという点です。問題を解いて確認をしてみましょう。

　文章をよく読むと、2/7のもとになっているのは「全体」で、4/5のもとになっているのは「(全体から1日目の分を引いた)残り」だとわかります。このことを考えて、丁寧に図をかくと(図1)のようになります。
　　

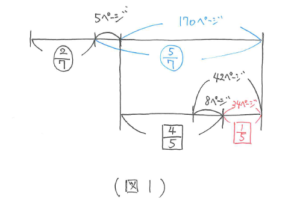
　全体から1日目の分を引いた残りは(42－8)÷(1－4/5)＝34÷1/5＝170(ページ)と計算できます。よって、全体は(170＋5)÷(1－2/7)＝175÷5/7＝245(ページ)と求まります。
　割合の問題は文章が複雑になっても、「割合」→「もとにする量」と考えることは変わりません。しっかり練習していきましょう。

【第1位　平均算：「平均×個数＝全体」の関係を面積図で整理できていますか？】

　平均の問題で「数量の合計＝平均×個数」の関係を使って計算し、途中で行き詰まってしまうときは、面積図を使うと解くことができます。面積図のかき方は、たてに「平均」を書き、横に「個数」を書きます。すると、たて×横で計算できる面積が「数量の合計」になります。次の問題で練習してみましょう。

　条件を図にかきこむと、(図1)のようになります。
　　

　平均とは「平らに均す」ことですから、(図1)のアの部分とイの部分の面積が等しくなっています。
　よって、(150－110)×20＝(110－100)×□、□＝80(冊)となります。この80冊は100円で買った冊数なので、買ったノートは全部で20＋80＝100(冊)と求まります。
　このように面積図を使うとあっさり求めることができます。計算で行き詰まったら、すぐに面積図を思い出して使っていきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。