メールマガジン宝箱 Mail magazine

　いよいよ4年生最後の組分けテストですね！これまでに習った単元が範囲なしで出題される手強いテストですが、クラスアップに制限がありませんので今よりも上位のクラスで5年生のスタートを切る大チャンスのテストです。そこで1月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　計算の工夫：11から15の数の平方数は覚えられていますか？】

　組分けテストでは解ける問題を確実に得点することはもちろん、解答にかける時間をどれだけ短縮できるかが、テスト全体の得点をアップさせるために不可欠となります。
　そこで計算の工夫方法をどれだけ覚えられているか、テスト前にチェックしておきましょう。特に、平方数（同じ数のかけ合わせ）について、11×11から15×15の計算結果までは確実に覚えておきたいところです。この平方数は円とおうぎ形の面積の計算「半径×半径」で使うだけでなく、数列などの規則性の問題でも使うことがあります。例えば、121，144，169，…といった数の並びを見た瞬間に、これが平方数を順に並べた数列であると気づくことができれば、解答にかける時間を大きく圧縮できます。
　また、0.125＝1/8，0.375＝3/8，…といった「1/8シリーズの小数と分数の変換」も覚えておくと、計算を速く正確に解けるようになりますので、1/4シリーズと合わせて、しっかり暗記を確認しておきましょう。

　こうした計算の工夫や覚えておくべき計算の結果を身につけておくことは、今回のテストの点数を安定させるだけでなく、これからの算数のテストで差がつくポイントのひとつとなります。速く正確に計算を行えるように、今のうちに練習を重ねておきましょう。

【第4位　面積図の活用：平均算、つるかめ算だけでなく過不足算でも使える強力な武器です！】

　テストの前半に出題される文章題の小問集合でどれだけ得点を重ねられるかが、今回の組分けの偏差値をアップさせるポイントになります。そうした文章題を解くにあたって面積図を活用することは、問題で何を求めるのかを視覚的にも把握できる効果があり、問題内容を正確に把握でき、結果として得点力を大きく上げることにつながります。
　面積図といえば、平均算やつるかめ算で用いることが多いですが、それ以外の単元、例えば過不足算でも面積図は大いに有効になるのです。例えば「ミカンを1人あたり4こずつ配ろうとすると18こあまり、１人に7こずつ配ろうとすると15こ足りなくなる」といった過不足算の基本パターンで、ただ式の立て方を暗記するのではなく、図で問題内容を整理することによって、視覚的に問題内容をイメージすることができて、式の意味を深く理解することができます。そうなれば、問題の出された方が変わっても、落ち着いて対応できるようになります。

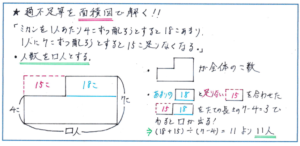
　面積図はこれから使う場面がドンドン多くなって行きます。新5年生になって割合と比の問題はもちろん、速さや比の問題でも面積図はその威力を発揮します。まだ面積図のかき方そのものが身についていない場合は、少し時間をかけても構いませんので、じっくり書き方から復習してみてください。これからの算数の難問を攻略するための強力なアイテムを手にすることができます。

【第3位　速さ：基本公式は間違いなく覚え込めるように徹底的に練習を重ねましょう！】

　この組分けテストから、いよいよ「速さ」がテストの範囲に含まれるようになります。組分けテスト自体には範囲はありませんが、授業で速さを習っていますので、今回のテストでも出題される可能性はとても高いです。「速さ」は中学受験算数の最頻出単元のひとつです。今後、速さの応用問題を解くことになる前に、まずは今の段階で「速さの意味」を理解しておく必要があります。
　例えば「時速40㎞」は1時間あたり40㎞進む、という意味になります。親御様からすれば当たり前に思われるかもしれませんが、この速さの根本的な意味を理解しないままに、暗記で答えようとすると式の立て方で間違えるケースがとても多くなるのです。
　この意味を理解できていれば、「時速60㎞は秒速何mか」といった単位換算の問題（間違える生徒さんがとても多い問題のひとつです）で迷わず式が立てられるようになります。時速→1時間あたりに進む道のり、秒速→1秒あたりに進む道のり、とすることで、まず時速よりも秒速の方が数値が小さくなる、どれだけ小さくなるかと言えば、時間から分で1/60、分から秒で1/60と、式につながる考え方ができるようになります。これをただ1/60×1/60という式を暗記するだけでは、問題の聞き方が少し変わってしまうだけで、急に解けなくなってしまう、という事態になってしまうのです。

　そのうえで、速さの基本公式である「速さ×時間＝道のり」を徹底的に覚え込んでおきましょう。この公式さえ覚えておけば、「速さ＝道のり÷時間」、「時間＝道のり÷速さ」の式にも対応できるようになります。もちろん、3つの式ともに覚えておけば万全ですが、道のりを求める式を覚えておけば、上に示したような還元算の考え方で、速さ、時間を問われても、しっかり答えられるのです。
　5年生からは、速さの問題はまさに加速度的に難しくなって行きます。まずは基本公式を間違えなく答えられるように練習を重ねておきましょう。

【第2位　平面図形：円の中にある三角形の特徴をつかみとりましょう！】

　円とおうぎ形の問題では、単純に弧の長さやおうぎ形単体の面積を求めるような基本レベルの問題だけでなく、四角形や三角形と組み合わせたような問題で正確に得点することが必要になります。特に円の中に三角形が含まれるような問題では、三角形の辺が半径になった場合に二等辺三角形が作られることが多いので、辺の長さの関係をしっかり見つけるようにしましょう。
　また、三角形の角度の問題では外角の性質も見逃さないように注意してください。もちろんこの性質を使わないでも、ひとつひとつ角度を求めて行くことで正解にたどり着くことはできます。それでも外角の性質を使った解き方は、計算自体は簡単ですので短い時間で正解を得られるメリットがあります。

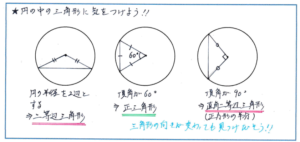
　組分けテストでは、とにかく少しでも時間を短縮して、かつ正確さを失わないような解き方が求められます。円とおうぎ形の問題は頻出の単元ですので、図形の中から短い時間で正確にヒントをつかみとれるような見方を少しでも養っておく必要があります。そのためには自分で図をかいてみることがひとつの有効な練習になります。問題の図を写すだけでも、辺どうしの関係や、同じ角度の関係など、図形の特徴がつかみやすくなります。ぜひ手を動かして図の内容を理解する練習をしてみてください。

【第1位　規則性：書き出しをして規則を見つけ出しましょう！】

　数のならび方の規則を求める問題では、頭の中だけで規則を見つけようとするのではなく、数のならびを自分で書き出してみる方が断然解きやすくなるケースが多くあります。
　例えば、「2,4,6,8,10,12,…」のような、一見してすぐ偶数のならび（差が2の等差数列）と判断できる場合や、「1,3,9,27,81,…」と、3倍ずつ数が増えて行くような数のならびであれば、わざわざ書き出しをしなくても、規則を見つけられます。むしろ書き出しに時間をかけるのは、限られた時間内に多くの問題を解かなければばらないテストでは、避けるべきでしょう。
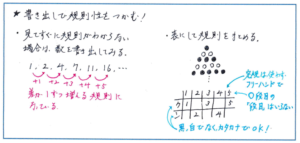
それに対して、例えば、「1,2,4,7,11,16,…」といった場合はどうでしょうか。規則性の問題をまだ数多く解いていない4年生の段階では、この数のならびの規則を瞬時に判断することは難しいでしょう。そこでとなり合う数の関係に注意しながら数を書き出してみましょう。すると、1→2で1増加、2→4で2増加、4→7で3増加、7→11で4増加、11→16で5増加、と差が1ずつ増える規則になっていることがわかります。
また、下の図にあるような、ご石などの図形がならんだ問題では、こ数の関係を簡単な表にすることで、規則を整理できます。白のご石が奇数段目に、黒のご石が偶数段目にあることをわかりやすくするために、白のご石と黒のご石それぞれの表を作るのではなく、どちらも合わせたものにすることで、規則をより正確に知ることができます。
　表をかく場合には、ていねいになり過ぎないように注意しましょう。大事なことは数の関係をつかむことで、キレイな表をかくことではありません。くり返しになりますが、制限時間のあるテストでは作業は「雑にならない限り速く進める」を念頭に置いておきましょう。

　書き出しは手間がかかりますし、面倒に感じるかもしれません。ただ、サピックスのテストでは特に終盤の問題で、「書き出す→問題の条件・規則を見つける→式を立てて計算を行う」といった作業を、速く正確に進める力を試す問題が、これから学年が進むにつれてドンドン多くなってきます。今の段階から手を使って問題内容を把握する習慣を身につけられるように、練習を重ねておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。