メールマガジン宝箱 Mail magazine

　いよいよいよいよ新6年生になる前の最後の組分けテストです！これまでに習った単元が範囲なしで出題され、難問も出題される可能性の高いテストですが、クラスアップに制限がありませんので今よりも上位のクラスで6年生のスタートを切る大チャンスのテストです。そこで1月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　基本ルールの確認：3.14計算、倍数のきまりなどは覚えられていますか？】

　テスト全体の点数をアップさせるには、計算問題を含めた前半の問題で少しでも多く得点を重ねることが必須です。そのためにも公式などの基本ルールを確実に覚えられているかどうか、テストの直前までにぜひチェックしておきましょう。
　例えば計算問題では、1/8＝0.125、1/4＝0.25といった分数から小数への変換がサピックスのテストでは頻出で、数字を見てすぐに変換できるかどうかが、点数を下支えするだけでなく、後半の問題に少しでも時間を割くことができるかの分かれ目になります。また、3の倍数であるための条件が、各位の数字の和が3の倍数であることといった倍数のきまりは、カードを使った場合の数の問題などを解くには不可欠になりますし、円とおうぎ形の問題を解く時間を大きく短縮させるには、3.14計算の結果（1ケタの数×3.14）を覚え込んでおけるかどうかがポイントになります。

　基本ルールでまだ固まっていないところがあるお子様は、紙にまとめて部屋やトイレに貼ってみることも有効でしょう。覚えられているかどうかがテスト結果に大きな差を生み出す基本ルールを、いま一度見直してみてください。

【第4位　平面図形：辺の長さの比の関係から解法を見つけ出しましょう！】

　平面図形では、比を使って解く問題が次第に多くなってきます。実際の入試問題では相似と面積比をはじめとした、比を使った平面図形の問題は頻出で、サピックスのテストでも比を使った問題を数多く出されることになります。
　例えば三角形の面積比において、高さが共通であれば面積比＝底辺比となることは基本中の基本として確実に覚えたうえで、底辺に平行な直線上を頂点が移動する場合には面積が変わらないという「等積変形」もすぐに対応できるようにしておく必要があります。問題によっては自分で平行な線を補助線として加えることも求められますので、底辺に平行な直線を見逃さない意識は常に持っておきましょう。
　また、底辺も高さも異なる図形どうしの面積比を求める際に、面積の公式に比を当てはめることで、単純な計算で正解を得られます。下の図で、平行四辺形ＡＢＣＤと三角形ＥＦＣの面積比を求める際に、平行四辺形の対角線ＢＤを結ぶ線を入れて、三角形ＥＦＣの面積を、平行四辺形ＡＢＣＤ×1/2×3/5×1/3と、三角形ＢＣＤの面積を利用して解くことができますが、それ以外の解法も身につけておくと、出題パターンが変わった際にも対応できるようになります。
　平行四辺形ＡＢＣＤの面積を、「底辺×高さ」の公式に比をあてはめて「5（底辺）×3（高さ）」と、三角形ＥＦＣの面積を「底辺×高さ÷2」の公式にやはり比をあてはめて「3（底辺）×1（高さ）÷2」とすることで、15：3/2＝10：1と簡単に正解に至ることができます。分数計算が苦手な生徒さんはぜひ覚えておくとよい解法です。

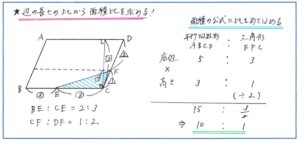
　これからの算数の問題では「比の重要性」がドンドン高まってきます。比を使った解法は多く覚えておくに越したことはありません。普段使っている解法以外でも使えそうな解法があれば、積極的に取り入れて行くようにしましょう。

【第3位　立体図形：水深変化は断面図で解決しましょう！】

　立体図形の中で、水そうの中におもりを沈めるような水深変化の問題で、断面図を使って解く方法はしっかり身についているでしょうか。断面図のかき方に少しでも曖昧なところがある場合には基本的なかき方から復習をしておくようにしましょう。この単元は4年生の後期に習って以降、何度か解くことがあったかと思いますが、この時期になると、比を使うことでより一層速く正確に解き進められるようになります。
　まずは以下の基本的な流れを確認しておきましょう。
正面から見た図（断面図）をかく。
→横の長さは「底面積」の大きさを表す。
→もとの水面をかく。
→おもりを入れた新たな水面をかく。
　そのうえで面積図と同じように、「同じ面積の長方形のたての長さと横の長さは逆比の関係にある」ことを利用して解き進めて行くことになります。
　つまり、図の（ア）の面積と（イ）の面積が同じですので、（ア）と（イ）の高さの比が1：6であれば、横の長さの比、つまり底面積の比が6：1になり、おもりの底面積を240×1/6＝40より40平方cmとして求めることができるのです。

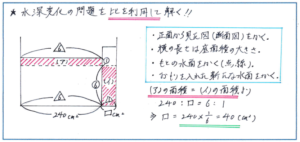
　もちろん（ア）部分の水の体積を求めて計算で解くこともできるのですが、底面積や高さが大きな数になってしまうと計算間違いを起こしやすくなってしまいます。比を習得することには多くのメリットがありますが、複雑な計算を回避できるという点もそのひとつなのです。比を使った解法を少しでも使いこなせるようにしておきましょう。

【第2位　規則性の問題：書き出しを使いこなせていますか？】

　テストの問題の中には、解法のヒントをつかむために「書き出し」が必要になる場合が多くあります。速さの問題で図をかくように、書き出しをすることで問題内容を整理することができるのです。
例えば、規則性の問題で「午前8時ちょうどから、5分おきに光る赤いランプと、午前8時ちょうどから、6分おきに光る青いランプがあります。赤いランプと青いランプが光る時刻が1分ちがうことは、午前8時ちょうどから午前11時20分までに何回ありますか」という問題があるとします。
　これが「同時に光る」という問題であれば「5と6の最小公倍数である30の倍数」を探せばよいので、すぐに式を立てて計算で解き進めることができます。それが「1分ちがう」という要素が入ってしまうことで、問題が複雑になっているのです。こうした場合、頭の中だけで解こうとするとミスが起こってしまいがちです。
　そこで、赤いランプと青いランプが光る時刻を実際に書き出してみましょう。赤いランプは、0、5、10、15、20、25、30、35…と数が並びます。一方の青いランプは、0、6、12、18、24、30、36…といった数の並びになります。こうして書き出してみると、5と6の最小公倍数である30分がひとつの周期になっていることがわかります。その中で「5と6」、「25と24」の2回があてはまり、午前8時ちょうどから午前11時20分までが3時間20分＝200分になることから式が立てられます。200÷30＝6あまり20より、30分の周期が6回あることから2×6＝12（回）、さらにあまりの20分の中に「5と6」が1回あるため、1を加え、12＋1＝13（回）と答えに行き着くことができるのです

　上記のような問題以外にも例えば数の性質の問題で、書き出しでなければ解決できない問題、書き出しが有効になる問題が多くあります。「4で割って1あまり、7で割って3あまる数」のように、あまり共通でも、不足共通でもないパターンでは、それぞれに当てはまる数を書き出して、どちらにも当てはまる最初の数「17」を見つけ、そこから4と7の最小公倍数28ずつ数が増えて行く、という解法で進めることになります。
　書き出しは手間がかかるようですが、問題内容を正確に整理するには効果的な手段であり、また特にサピックスのテストでは、書き出し→法則性を見つける→式を立てる、といった流れで解く問題が終盤の応用タイプで出されることが多くあります。書き出しは有効ですが、雑に対応してしまうと見逃しなどのミスにつながります。速く見やすく書き出しができているかどうか、しっかり見直しておきましょう。

【第1位　速さの問題：ダイヤグラムをつくる時間を短くする工夫はできていますか？】

　速さの問題もこの時期になると、問題内容の複雑さが一気に増してきます。そうなると必要なのが、図での内容整理ですが、図をいかに使い分けるか、また限られた時間の中でどれだけ簡潔に、かつ内容をまとめる図をかけるかがポイントになります。
特にダイヤグラムは、往復運動などの問題を整理する際には圧倒的に有効ですが、完成させるのに多大な時間がかかってしまう可能性も高くなります。ダイヤグラムをかかなくても線分図で十分に内容を整理できるか、ダイヤグラムをかくにしても、問題内容すべてを表す必要があるのか、といった点を考えられるように、図に対する意識づけを高めておきましょう。
　問題のポイントになる部分に絞ってダイヤグラムをかく際の注意点としては、求める時間や距離が含まれる部分であることはもちろんですが、できるだけ変化の少ない範囲に絞ることが重要です。特に速さが一定の範囲に絞ることができれば、断然解きやすくなります。同じ地点からそれぞれ一定の速さで動く、といった変化の少ない部分であればダイヤグラムもかきやすくなります。絞り込む部分がなかなか絞れない場合は、まずはダイヤグラムの全体像を雑なかき方で構いませんのでかいてみて、その上で注目すべき部分を絞ってもよいでしょう。

　ダイヤグラムは、速さや進行方向の変化をひとつのグラフのかたちにまとめられ、また相似を利用した解き方ができる点で大きなメリットがありますが、そのすべてを限られたテストの時間内にかき上げようとすると気持ちの負担も大きくなり、焦った挙句に解答の方針が立たない、という事態に陥ってしまうこともあります。テストまでに、できるだけ多くダイヤグラムを見て、ポイントを絞ったダイヤグラムに対するイメージをしっかり固めておくとよいでしょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。