メールマガジン宝箱 Mail magazine

　新6年生になって最初の組分けテストです！まだ新年度が始まって間もない時期で、新たなカリキュラムに対応するだけでも大変な状況ですが、クラスアップに制限がない組分けテストですので今よりも上位のクラスにジャンプアップできる大チャンスを勝ち取りたいところです。そこで3月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　立体図形の問題：展開図を見るポイントは身につけられていますか？】

　立体図形の中で、展開図の問題は難度こそ決して高くはないのですが、速く正確に解く方法をしっかり身につけていないと、思わぬ失点や時間のロスにつながってしまうことがあります。展開図の問題を確実な得点源にできるように、図の成り立ちをしっかり確認しておきましょう。
　展開図の問題で、組み立てた際に重なる点を求めるタイプのものがあります。例えば下の展開図の点Ｍと重なる点を考える問題であれば、点Ｌを中心に90度回転した点Ｋが該当することは、すぐに求められます。展開図を組み立てるイメージをした場合に、90度回転した点が重なることは思い浮かべやすいでしょう。
　ところが、点Ｅと重なる点となると、すぐに思い浮かばないかもしれません。点Ｅの位置では「90度回転」の考え方が使えないため、点の位置関係が一気にわかりづらくなってしまうのです。
　そこで「立体上で最も遠い点は、展開図の2つの正方形でできる長方形の対角線上にある。」という考え方を使ってみましょう。立体の面を図のように広げてみるとわかるでしょう。そこで、展開図で点Ｅから対角線の位置にある点Ｌが見つけられます。さらに「最も遠い点から見て最も遠い点は、もとの点に戻る」ことに気づけば、点Ｅに重なるのが点Ａ、点Ｉであると、難なく正解に行き着くことができます。

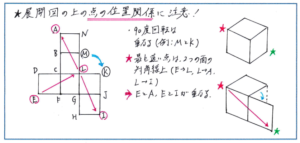
　展開図の問題を正確に解くためには、平面図形から立体図形を正しくイメージできるかどうかがポイントになります。実際に展開図を自分で作って組み立てるという練習方法もありますが、平面図形のままの状態で点の位置関係が把握できるように練習を重ねておきましょう。

【第4位　規則性の問題：数表問題に正確に対応できていますか？】

　規則性の問題の中で、例えば等差数列や、グループ数列といった数が横並びになるパターンではなく、数字が表のかたちになっている場合、その規則の読み取りにはより慎重に取り組む必要があります。　　
　特に「数字が増減する向き」には十分に注意しなければなりません。左の図のような、数が増えるにつれて行や列が改まるかたちであれば、数の位置は求めやすくなります。それに対して右の図のような数のならびになると、偶数列では数が上から下に増えて、奇数列では下から上に数が増えるといった規則になります。この向きを正確にとらえられていないと、問題を解く際に混乱してしまい、得点のチャンスが大きく減ってしまいます。数字の増減の向きには細心の注意を払ってください。
　また、こうした数表の問題では「平方数（同じ数をかけ合わせた数）」が、どの位置にあるかに注目してください。右の図では2行1列に4（2×2）、1行3列に9（3×3）、4行1列に16（4×4）、と、偶数行1列、1行奇数列に平方数があることがわかります。この平方数の位置が、問題で求める数の位置を答える際に大きなヒントになるのです。

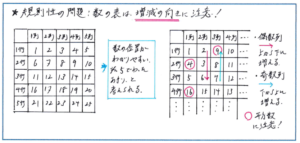
　規則性の問題では、数の書き出しなど手を動かして規則を見つけ出す作業が必要となるケースが多いですが、これから問題の難度が上がって行くと、書き出しよりも前に、まず数の位置関係などといった規則がどのようなものであるかを短い時間でかつ慎重に考えてから、書き出しでその規則を確かめるといった流れで進める必要が出てくるのです。数の並びのどこに注目するかを意識して問題演習をくり返しましょう。

【第3位　平面図形：円・おうぎ形の半径の長さが等しいことを利用できていますか？】

　平面図形の問題は、新6年生になって図形の複雑さが増して行きます。特に、異なるタイプの図形が組み合わさってできる「複合図形」の問題はその数が格段に増えてきます。その中でも、円やおうぎ形が組み合わさってできる図形では、半径が同じ長さであることを利用するケースが多くなります。
　下の図は正方形の中に2つのおうぎ形がかかれたかたちです。点Ｂを中心としたおうぎ形の半径であることから、ＢＣの長さとＢＥの長さが等しくなり、点Ｃを中心としたおうぎ形の半径であることから、ＢＣの長さとＣＥの長さが等しくなります。そこでＢＣ＝ＢＥ＝ＣＥより、三角形ＢＣＥが正三角形であるとわかるのです。この三角形ＢＣＥのかたちが直感的に正三角形であると何となくイメージできるかと思われます。算数では直感はとても大事ですが、直感だけで問題を解き進めることはできません。根拠をしっかりと持てるように、長さの関係には十分に注意して問題に取り組みましょう。

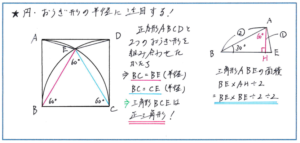
　また上の図ではもう1つのポイントがあります。三角形ＡＢＥ、三角形ＣＤＥの面積をスムーズに求められますでしょうか。この2つの三角形はＡＢ＝ＢＥ、ＣＤ＝ＣＥであることから二等辺三角形となり、頂角（角ＡＢＥ、角ＤＣＥ）は90－60＝30（度）となります。この頂角30度の二等辺三角形の面積の求め方をしっかりと見直しておきましょう。三角形ＡＢＥであれば、点ＡからＢＥに垂直な線分ＡＨを下すことで、面積はＢＥ×ＡＨ÷2の式で求められます。三角形ＡＢＨが「90度、60度、30度」の正三角形を半分にしたかたちですので、ＡＨの長さはＡＢの長さの半分となり、ＢＥ×ＢＥ÷2÷2と求めることができるのです。
　二等辺三角形のうち、頂角が30度の場合の面積の求め方は頂角150度の場合でも使えます。これらの二等辺三角形が見つけられた際には、すぐに、面積の求め方が浮かぶように練習を重ねておきましょう。

【第2位　比の問題：逆比の関係を利用すれば断然解きやすくなります！】

　文章題の中には、比、特に逆比の関係を利用することで、解く速さと正確さに大きな差を生むことができる問題があります。
例えば「キャラメル7個とクッキー10個の値段の合計は1230円で、キャラメル2個の値段とクッキー3個の値段が等しいとき、クッキー1個の値段はいくらですか。」といった問題があるとします。
　2種類の品物があり、それぞれの1個あたりの値段と合計金額、そして値段の関係がわかっているので、消去算で解く方法が浮かんでくるでしょう。実際に、クッキーの値段で統一するために、キャラメル×7＋クッキー×10＝1230の式のキャラメルの部分をクッキーに替えるように、消去算の代入法で解くことができます。キャラメル14個の値段がクッキー21個の値段と同じになるので、キャラメル×14＋クッキー×20＝2460の式のキャラメル×14をクッキー×21に入れ替えて、クッキー×21＋クッキー×20＝クッキー×41＝2460よりクッキー1個の値段が、2460÷41＝60（円）と求めることができます。ただし、式を2倍することで数が大きくなり、計算ミスなどが起こりがちにもなってしまいます。
　そこで、キャラメル2個の値段とクッキー3個の値段が等しいことから、キャラメル×2＝クッキー×3＝1という式が立てられ、そこから、キャラメル×1/2＝クッキー×1/3より、キャラメル1個の値段：クッキー1個の値段＝3：2の比例式を導くことができます。あとは、キャラメル1個の値段をマル3、クッキー1個の値段をマル2として、キャラメル×7＋クッキー×10＝1230の式をマルで表すと、マル21＋マル20＝マル41＝1230より、マル1＝30から、クッキー1個の値段はマル2＝60円と求められるのです。

　この問題に限らず、速さや図形の問題でも逆比の考え方は有効に使えることがあります。特にこれから問題の難度が上がると、いかに速く、間違いが少ない解法を使えるかが偏差値アップのポイントになります。逆比の関係を使った解法を活用できるように練習をしておきましょう。

【第1位　平面図形：相似の関係を見つけ出すことはできていますか？】

　先程も書きました通り、6年生になると平面図形の複雑さが急速に増してきます。その中でも比を使った問題は出題頻度が高く、図形の中からいかに速く正確に比の関係をつかみとるかが得点力アップの大きなポイントになります。
　平面図形と比の問題では、「高さ共通の図形での面積比は底面比と等しい」そして「相似」という2つの要素をいかに的確に使いこなすかが得点差を作り出すきっかけとなります。また、その2つの要素どちらをも使う問題も数多く出されます。
例えば下の図で、長方形ＡＢＣＤの中に線分をかきいれることでできた三角形ＨＩＧの面積に注目すると、ＥＨとＦＧが平行であることから、三角形ＥＨＩと三角形ＧＦＩは相似の関係になり、ＥＩ：ＧＩ＝ＥＨ：ＦＧ＝3：5となります。ここまでは相似の関係で導くことができます。
　そして三角形ＥＨＩと三角形ＧＨＩの関係を見ると、それぞれの底辺をＥＩ、ＧＩとすると高さが共通になるため、三角形ＥＨＩの面積：三角形ＧＨＩの面積＝ＥＩ：ＧＩ＝3：5と、底辺比を利用して解き進められるのです。

　こうした平面図形と比の問題を正確に解き進めるためには、底面比や相似の基本パターンをいかに多く頭の中に植え付けておくかが重要なステップになります。上の図でも三角形ＥＨＩと三角形ＧＦＩは相似の中でも基本的な砂時計型のパターンになっています。平面図形と比の基本パターンが定着していれば、問題の図を見てすぐに「ここが相似になれば解きやすくなる」といった解法の羅針盤を自分の中につくることができます。そうなれば、相似になるためにはどの辺、どの角度に注目をすればよいかといった、思考をさかのぼるかたちで問題の要素を見つけれられるようになるのです。
　実際の入試でも頻出の平面図形と比の問題を攻略するためには、図形のパターンに慣れることです。ただ漫然と図形を見るのではなく、どこかに相似や底辺比を使える部分はないか探し出す意識を強く持って問題に臨むようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。