メールマガジン宝箱 Mail magazine

　新5年生になって最初の組分けテストです！クラスアップに制限がない組分けテストで上位のクラスにジャンプアップするためにも、偏差値アップのポイントとなる問題は確実に得点できるよう、万全の準備をしておきたいところです。そこで3月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　単位換算：面積・容積の単位換算を正確に覚えられていますか？】

　単位換算を正確にできているか確認しておくことは、テスト序盤の単位換算そのものを求める問題で確実な得点をするための対策にとどまりません。例えば立体図形の深さの変化の問題では、水の容積がリットルで表されるケースが少なくありません。そうした場合、リットルから立方cmへの変換をできるだけ速くできれば、時間と得点に差をつけることにつながります。
　単位換算の覚え方としては、1リットル＝1000立方cmと数を暗記するのでもよいですが、下の図のように「1リットルは1辺10cmの立方体の体積」と立方体の形を利用すれば、視覚的に覚えられる効果があります。

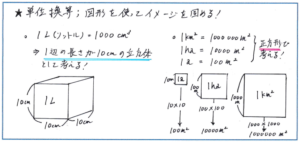
　この図形を使った単位換算の覚え方は、面積の平方m、a（アール）、ha（ヘクタール）、平方kmの換算でも使うことができます。ほんの些細な内容に見えますが、確実に覚えておくかどうかで、思っている以上に得点差を生み出します。新5年生になった今のタイミングこそ、この単位換算が確実に覚えられているかどうか、組分けテストまでにチェックしておきましょう。

【第4位　平面図形：半径がわかっていない円の面積を求められていますか？】

　平面図形の問題は学年が進むにしたがってその難度が増し、図形の成り立ち自体が複雑になってきます。単純な三角形や四角形、円・おうぎ形の面積を公式によって求めるような基本パターンの数は減り、かわりに円・おうぎ形と三角形や四角形が合わさった「複合図形」の問題が多くなってきます。そうした際には図形を見る角度を切り替えたり、補助線を引いて図形を切り取るなどのひと工夫を加えて、自分が使いこなせる基本パターンに持ち込む必要があります。
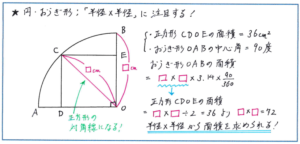
　また、図形の面積を公式で解く際に、使いたい長さがわからない場合があります。その代表格が「半径の長さがわからない円・おうぎ形の面積」です。図のように半径の長さがわかっていないおうぎ形の中に正方形がぴったりと入っているかたちを例に考えてみましょう。
　おうぎ形の面積は半径×半径×3.14×中心角/360度の公式で求められますが、この半径×半径の部分に注目します。もちろん半径の長さがわかっていれば、その値を公式にあてはめることができますが、半径の長さがわかっていなくても、「半径×半径」の値がわかれば解き進めることができます。この図形であれば、おうぎ形の半径と同じ長さになるのは正方形の対角線の長さです。半径×半径を、対角線×対角線に置き換えると、見覚えのある面積公式に近くなります。ひし形の面積の公式は「対角線×対角線÷2」ですが、正方形はひし形の一部（正方形はひし形の内角が90度の時の図形です）ですので、図の正方形の面積が36平方cmであることから、対角線×対角線÷2＝半径×半径÷2＝36より、半径×半径＝36×2＝72と求めることができるのです。よって、おうぎ形の面積は72×3.14×90/360＝18×3.14＝56.52（平方cm）と正解にたどりつくことができます。

　どの単元にもあてはまることですが、算数の問題で少しでも多く得点するには、解法をできるだけ多く持っておく必要があります。そのためにも、解答の方針を自分の知っている基本パターンに持ち込むにはどうすればよいか、その意識を強く持って問題に臨むようにしましょう。

【第3位　つるかめ算の応用：弁償算の問題は図で内容を整理しましょう！】

　つるかめ算と言えば「1本100円のえんぴつと1本120円のボールペンを合わせて20本買ったところ2160円になりました。えんぴつは何本買いましたか。」といった基本パターンがありますが、その応用型として、次のようなパターンがあります。
　「ガラス皿を100枚運びます。1枚運ぶと20円もらえますが、ガラス皿を割ってしまうと1枚につき80円弁償しなければなりません。ガラス皿を運び終えたとき、500円もらいました。全部で何枚のガラス皿を割ってしまいましたか。」といった問題。
　つるかめ算の基本的な考え方は、1つ入れ替えることでどれだけの差が生まれるか、という点にあります。最初に挙げた例であれば、ボールペン1本とえんぴつ1本を入れ替えると120－100＝20（円）の金額の差が生まれます。そこで、「仮に20本すべてがボールペンだったとする」の考え方を使い、120×20－2160で求められる仮の場合と実際との金額の差を、1本あたりの金額の差120－100＝20（円）で割ることで、(120×20－2160)÷(120－100)＝12より、入れ替えた回数が12回、つまりえんぴつの本数が12本と求めることができます。
　この応用パターンは「弁償算」とも言われますが、この弁償算でも基本的な考え方は変わりません。「仮に1枚も割らなかった」として、そこで生まれる実際の金額との差を、1枚割ることで生まれる金額の差で割ることになります。ここでポイントになるのが、1枚割ることで生まれる金額の差が、基本パターンのような金額の差（引き算）ではなく、「金額のたし算」として求めるところにあります。この差がたし算になるという点をよりわかりやすくするために、下の図のような図を用いるとよいでしょう。この図を横にしてもよいのですが、たてにする方が温度計のイメージでとらえることができます。

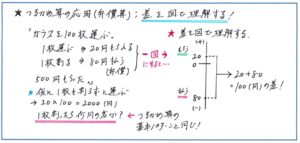
　式としては、20×100－500で仮の場合と実際との金額の差を求めるところまでは基本パターンと同じで、1枚あたりの差を20＋80＝100と、たし算にしてすることに注意しましょう。(20×100－500)÷(20＋80)＝15より、割ってしまった枚数は15枚と求められます。
　つるかめ算の基本パターンでは面積図を有効に使えましたが、この弁償算のパターンでは面積図をかくこと自体が難しくなります。つるかめ算であれば面積図と思いこむのではなく、問題内容を整理するために図を使うことを念頭に置いて、そこから式を立てる流れで解き進めるとよいでしょう。

【第2位　平面図形：同じ面積を見つけ出すことができていますか？】

　平面図形の面積の問題では、同じ面積（等積変形）を速く確実に見つけ出すことが得点力アップのポイントになります。三角形の面積において、「底辺と平行な直線上に頂点がある場合は面積が等しくなる」という性質を使った問題は、特に台形や平行四辺形の中での三角形の面積を求めるタイプとして多く出されます。台形も平行四辺形も向かい合う辺どうしが平行の関係にありますので、この等積変形が成り立つケースが多くなるのです。頂点がどの位置にあっても底辺と高さの関係が変わらなければ面積は同じということが基本的な考え方となります。
　注意すべきは、底辺はいつでも水平の位置にあるとは限らないということです。図のように平行四辺形の辺上に三角形の底辺があることに着目して、その辺と平行な辺上に頂点があれば、頂点を移動させることができるという点を使って等積変形することで、三角形の面積が平行四辺形の面積の半分になるとわかるのです。

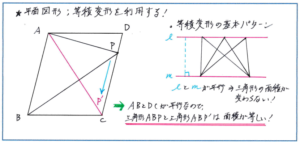
　慣れないうちは図形を回転させて三角形の底辺が水平になるように変えてみても構わないですが、できるだけ図形を回転させないままで三角形の底辺と高さの関係をつかめられるように練習を重ねておきましょう。これからサピックスのテストでは図形が様々なかたちで出題されるようになります。その度にテスト用紙を回転していては、時間がかかるだけでなく、少し図形が複雑になるだけで解き方が見つけられなくなってしまいます。与えられた図形のかたちそのままで、底辺と高さなどの長さ、あるいは角度の関係を速く正確に見つけられることを目標にしましょう。

【第1位　場合の数：「当てはまらない方を求める」解法を使えていますか？】

　算数の問題は単元に関わらず解きやすい方法を速く見つけ出すことがテストでの時間の短縮、それにより時間をかけたい問題に多くの時間を残すことができる効果につながります。特に場合の数は解き方によって計算の負担が大きく変わってきます。
　例えば「1、2、3、4の4つの数を使って4けたの数をつくるとき、1300より大きい整数は何個できますか」といった問題。まず思い浮かぶのは、千の位の値によって場合分けをして、それぞれの場合について樹形図であてはまる数を書き出すといった解法ですが、ここで一度立ち止まって頂きたいのです。もっと早く負担のない解き方がないかどうかを考えてみましょう。
　千の位に注目するのは間違いないことですが、1300より大きい整数の数を求めるためには、4つの数でできる4けたの数から「1300以下であてはまる数」を見つけて、その数を全体から引いても求めることができます。千の位に入る数だけを見ても、1300より大きい場合は1、2、3、4のすべてが当てはまるのに対し、1300以下とすればあてはまるのは1のみ、百の位も2のみと、かなり限定されることがわかります。

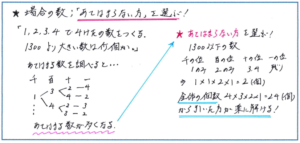
　その上で、全体の数、1300以下のあてはまる数がそれぞれいくつあるかを見つけ出すに際し、樹形図で書き出すこともできますが、計算で進める方法もしっかり確認しておきましょう。
全体の数は、千の位にあてはまる数が4個、百の位は千の位で使った数以外の3個、同じように十の位は2個、一の位は最後に残った1個となるため、4×3×2×1＝24（個）と求められます。
　1300以下の数は、千の位は1のみ、百の位は2のみ、十の位は1と2以外の2個、一の位は残りの1こで、2×1＝2（個）となりますので、1300より大きい数は、24－2＝22（個）となります。
　あてはまる数をそのまま求めようとすると、千の位が2、3、4の場合は、それぞれ3（百の位）×2（十の位）×1（一の位）なので、3×3×2×1＝18（個）、千の位が1の場合は、百の位は3か4、十の位は2個、一の位は残りの1個で、2×2×1＝4（個）で、合計して18＋4＝22（個）となりますが、各位にあてはまる数をもれなく見つけるには精神的な負担も大きくなります。さらにこれを樹形図でまとめようとすると、時間がかかり過ぎてしまうのです。
　場合の数を見てすぐに樹形図、とするのではなく、少しでも解きやすい方法がないか考える習慣を今のうちから身につけておきましょう。それはこれから問題の難度が上がる際に、より必要となる考え方です。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。