メールマガジン宝箱 Mail magazine

　今回の組分けテストは、「速さと比」「立体図形」といった、模試や実際の入試問題でも得点差がつく大事な単元が範囲に含まれます。図を使うなどの解法を使いこなして、これらの重要問題を確実に得点して、クラスアップのチャンスを逃さないようにしたいところです。そこで第2回組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！
　さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　素因数分解の利用：連除法の進め方だけでなく、どのような場面で利用するかを覚えておきましょう！】

　素因数分解を利用する問題としては、ある数の約数を求める問題がまず浮かびますが、それ以外にも様々な問題で利用する場面が出てきます。例えば、分数の約分で分子、分母の公約数を見てすぐに浮かばない際には、迷わず素因数分解を進めるようにしましょう。その過程を積んで行くうちに、数への慣れが生まれて、素因数分解を使わなくてもすぐに約分ができるようになります。
　また、約数の個数を求める問題では、約数を書き出すのではなく、素因数分解をした結果から計算で求める方法を定着させておきたいところです。6年生になると、約数の個数を求める問題で、その数が普段あまり接したことのないような値や、大きな数になることがあります。そうした場合は書き出しに多大な時間を要してしまいます。組分けテストでは時間はできる限り短縮する必要があります。素因数分解→（素因数の数＋1）のかけ合わせ、の流れがすぐに出てくるようにしておきましょう。

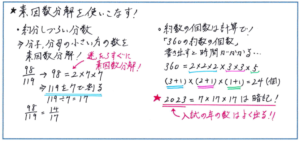
　約数の個数について、「2023」の約数の個数には徹底的に注意しておいてください。2でも割れず、3でも割れないこの数ですが、実は素数ではなく、「2023＝7×17×17」と素因数分解ができ、結果として約数の個数は、(1＋1)×(2＋1)＝6（個）となります。お気づきの通り、6年生の皆さんが受験をされるのは2023年です。入試の年に関する問題が出題されることはこれまでも多く見られ、特にこの「2023」は素因数分解にからめて扱われる可能性が高いと考えられます。素因数分解の結果を覚えていないと、かなり時間がかかってしまいますので、しっかり覚えておくようにしてください。

【第4位　立体図形：回転体の問題で、立体の相似比を使いこなせていますか？】

　立体図形の回転体の問題は、相似比を使いこなせるかどうかで、解答にかける時間と正確さに大きな差が生まれます。平面図形の面積比が（相似比×相似比）となることはすぐに浮かんでも、立体図形になるとうまく利用できない、という状況になってはいないでしょうか。その要因のひとつは、辺の比の関係が平面図形と比べて、立体図形ではイメージしづらいというところがあります。
　そこで、まずは回転体がどのようなかたちになるか、見取り図を正確にかくようにしましょう。正確とは言っても、長さなどを細かくチェックする必要はありません。長さの大小関係や、平行な線の関係を自分で把握できる範囲で構いませんので、まずはしっかり見取り図をかくようにしましょう。
　そのうえで、平行な線に注目して、相似の関係を見つけて行きます。ここで気をつけたいのが、回転体の問題でよく出されるの円すい台（プリンのような形）です。大きな円すいから小さな円すいを引いて体積が求められる立体ですが、ここで相似比が活用できるかどうかがポイントになります。例えば図のように小さな円すいと大きな円すいの相似比が2：3の場合、その体積比は（2×2×2）：（3×3×3）＝8：27となり、円すい台の体積は大きな円すいの、1－8/27＝19/27とすることができるのです。それにより、体積を計算する際に、9×9×3.14×18×1/3×19/27＝18×19×3.14と、かけ算のみの形にできます。

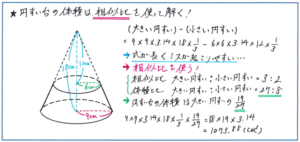
　計算の結果、このような約分がいつもできるとは限りませんが、大きな円すいから小さな円すいを引くといった計算では、分数計算が多くなり、思わぬところでミスを起こしてしまいます。相似比を利用することは計算ミスを防ぐ効果もありますので、相似の関係を見つけることを強く意識しながら演習を進めて行きましょう。

【第3位　旅人算：速さの和と差を見つけ出せていますか？】

　6年生の組分けテストになると、速さの問題も難度が上がってきます。比を使うタイプの問題が難問の代表例ではありますが、もう1点気をつけておきたいのが、つるかめ算や和差算といった文章題の考え方を利用する問題です。
　このうち、つるかめ算については、「6㎞の道のりを時速20㎞でスタートして、途中で速さを時速30㎞に上げ、合計15分かかりました。」といった、速さを変えるタイプの問題として出されることが多くあります。合計時間、速さを変える前後の速さ、合計の道のりといった要素がわかっていれば解ける、というパターンをしっかりおさえておけば、問題を見た瞬間に、つるかめ算を使う、という方針が立てやすくなります。
　一方、和差算を使う問題になると、問題を見た瞬間に和差算と結びつけることが難しいケースがあります。このタイプの問題でよく見られるのが、池の周りを2人が同じ方向に進んだ場合と、反対方向に向かい合って進んだ場合での時間の違いが説明されているパターンです。これを基本として、例えば折り返しや、十字型に進むといった応用パターンにまで出題内容が発展することがあります。大事なのは、速さの問題でも、和差算という他単元の考え方を利用するケースがあることを踏まえ、和と差がわかっていればそれぞれの値が求められるという和差算の基本概念をしっかりと頭の中に入れておくことです。そのうえで、旅人算の基本に立ち返って、どのような場合に速さの和や差が求められるのかを、認識しておきましょう。

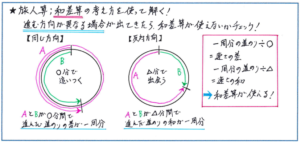
　これからのテストでは、速さなら速さの考え方だけ、といったシンプルな形での出題ではなく、様々な単元が入り混じった複合型の問題が出されるケースが多くなり、そうした問題を確実に得点できるかどうかが、偏差値アップの鍵となってきます。まずはそれぞれの単元の基本的な解法を確認したうえで、それらが複合的に出されることがある、という意識をもって演習に臨みましょう。

【第2位　立体図形：切断の問題で、面を延長させる解き方を覚えられていますか？】

　立体図形の中でも難問となる問題のひとつが切断です。かつては入試において、算数の難問を出す上位校での出題に限られていたこの切断ですが、現在では中堅校でも出題されることが多くなっています。ただでさえイメージが難しい立体図形の中でも、切り口の断面図は、慣れないうちはどのような形になるかが、なかなか頭に浮かんでこない難敵です。
切断面を正確にかく際のおさえるべきポイントは以下の3点です。
1.同じ平面上にある2点を結ぶ。
2.平行な面上にある切り口の線は平行。
3.足りない部分は平面を延ばして考える。
　このうち、最初の2点は基本演習のくり返しで定着させることができますので、まずはこの2点を頭の中に徹底的にすり込むように、基本問題を何度もくり返し練習しましょう。
ポイントは3点目の面を延長させる考え方です。角出し（つのだし）とも言われるこの考え方をマスターできれば、解ける問題の幅が一気に広がります。
　考え方としては、立体を部屋の隅に置いて、2面の壁と床に面が広がるとイメージするとよいでしょう。あとは線のかき込みをして行きますが、相似の関係を的確につかむためのかき込みですので、急ぎ過ぎず、平行線の関係をしっかり確認しながら進めて行きましょう。この過程を雑にせずに、正確に進めることが得点できるかどうかの分かれ目になります。

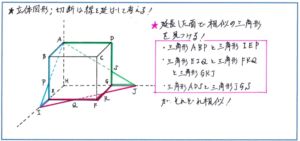
　この角出しタイプの問題で体積を求める場合には、先の【第4位】でご紹介した、相似の立体の解き方が必要になります。くり返しになりますが、大きな図形から小さな図形を引くという解法だけでなく、相似を利用した分数計算に持ち込めるようにいま一度確認しておきましょう。

【第1位　速さと比：比を使った解き方をフル活用するために図で内容を整理できていますか？】

　速さと比の問題では、一見したところ比を使うと思いつかないケースが多くあります。そうした問題では、線分図やダイヤグラムといった図をかくと、問題内容が整理され、比の関係を視覚的にとらえることができます。
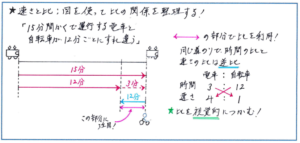
　例えば「電車の線路に沿った道を、自転車で一定の速度で走っている人が、15分間かくで運行している電車と、12分ごとにすれ違いました。電車の速さと自転車の速さの比を最も簡単な整数比で答えなさい。」といった問題を例にしてみましょう。電車が一定の間隔で運行することのイメージはできても、そこからどのように比に結びつけるか、頭の中だけで考えていては、なかなか思いつかないところです。
　そこで線分図で内容を整理してみましょう。電車が15分間隔で進む、というところをどのように図にするかですが、時間の差を線の長さで表現してみましょう。15分後に次の電車が出発する、ということは電車と次の電車の間には、15分にあたる道のりの差があると考えられます。同じように自転車の進む道のりを時間で考えてみると、電車と自転車が12分かけて出会う様子を図にすることができます。ここで、自転車が12分かけて進む道のりを、電車は(15－12＝)3分かけて進むことがわかります。あとは同じ道のりを進む場合、時間の比と速さの比が逆比になる、という基本に基づけば、電車と自転車の速さの比が、1/3：1/12＝4：1と求められます。

　頭の中だけで考えていてはつかみとれない関係性が、図を使うことですぐに理解できるというケースが、速さの難問では多くあります。線分図のかき方に抵抗を感じてしまっている、かえって時間がかかると二の足を踏んでしまっているような場合は、まずは手を使うことを惜しまず、また最初は時間をかけて構わない、という意識を持って作図に取り組んでください。慣れれば図をかく時間は大きく短縮できます。図を使いこなせれば、解答のプロセスをつかむことの負担は見違えるほど減って行きます。手を使って問題内容を整理する習慣を身につけましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。