メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、いくつかの単元を合わせた応用問題（和差算＋つるかめ算など）が出される可能性が高くあります。そうした応用問題で得点をかせぎ、前半の小問集合でも着実に得点を重ねるために、これまで習った各単元の基本内容がしっかり理解できているかどうかチェックしておきたいところです。そこで7月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第5位　場合の数：場合の数をたす場合とかける場合の区別はできていますか？】

　場合の数の問題では、最終的な答えを出すために、求めた場合の数を「たすのか、かけるのか」を瞬時に判断できるようにしておく必要があります。
　場合の数をたす典型的なパターンには、例えばカードの並べ替えで、「1、2、5、6、9の数字が入った5枚のカードを並べ替えて、3けたの数を作る時、偶数は何通りありますか。」といったタイプの問題があります。一の位に入る数で場合分けをして、2が入る場合は、4×3＝12（通り）、6が入る場合も12通りで、この結果をたして、12＋12＝24（通り）となります。ここでは、一の位に2が入る場合と6が入る場合が「同時に起こることがありません」ので、たし算をすることになります。
　ここでの「同時に起こらない」という意味があまりピンと来ない場合には、その逆の「同時に起こる」パターンを確かめてみると一気にわかりやすくなります。
　そのパターンの典型は、例えば「男子2人と女子3人の5人が1列に並ぶとき、男子が両はしにくる並び方は全部で何通りですか。」といったタイプの問題です。男子2人が両はしにくる場合の数は2×1＝2（通り）、男子にはさまれるかたちで女子3人が並ぶ場合の数は3×2×1＝6（通り）となります。この場合、男子が並ぶのと女子が並ぶのは「同時に起こる」ため、かけ算をして、2×6＝12（通り）となるのです。

　組分けテストは範囲がないために、幅広い単元から出題されます。限られた時間内に得点を重ねるためには、基本的な問題は時間をかけずに正確に得点する必要があります。ここでお話ししたような場合の数の問題はテストでも序盤の小問集合で出されることが多いので、確実に得点するために、たすのか、かけるのかといった判断は瞬時に迷わずできるよう練習を重ねておきましょう。

【第4位　規則性：数列の規則性は、まず並んだ2つの数の差から目を付けましょう！】

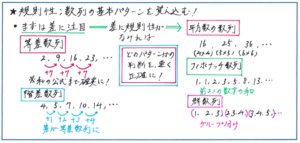
　規則性では様々な規則の数列の問題が出されますが、規則性を見つけ出すために、まずは並んだ2つの数の「差」に着目することから始めましょう。基本パターンの筆頭である等差数列、また差自体が等差数列になっている階差数列については、できれば問題を見た瞬間に判断をしたいところです。そのどちらでもない場合に、どのパターンの数列であるかをどれだけ早く正確に見つけ出すかが、テスト全体の得点を左右するポイントになります。
　真っ先に気づいておきたいのが平方数の並びです。5年生のテストであれば、平方数の数列は121（11×11）、144（12×12）、169（13×13）といった2けたの数の平方数よりも、16、25、36、…といった1けたの数の平方数が問題となり、規則性自体は基本レベルになるケースが多くなります。ただし問題は「19番目の数は何ですか」といった大きな数の計算になることもありますので、筆算をしっかりと行って計算ミスを起こさないように注意しましょう。
　差を使った数列、平方数の数列のどちらでもない場合には、前の2つの数の和が並ぶフィボナッチ数列や、いくつかの数のグループが規則的に並ぶ群数列といった数列になることが多いですが、こうした問題は規則性さえ見つけられれば、答えを求める計算自体の難度は上がらないことが多いです。それだけに規則性をしっかりと見つけられるように、それぞれの基本的なかたちをおさえておくようにしましょう。

　規則性の問題がテスト前半の小問集合に出てくる場合には、比較的得点がしやすくなる一方で失点してしまうと差がつけられてしまう問題にもなります。等差数列の和など基本公式の部分がしっかり覚えられているかどうか、テスト前にチェックしておきましょう。

【第3位　平面図形：図形の回転移動など、おうぎ形の中心が変化する問題に対応できていますか？】

　平面図形の中でも、例えば長方形の辺上を正三角形が回転する問題や、綱でつながれた牛や羊の動く範囲を求めるような問題では、おうぎ形のかたちを正確に求めることが必須です。特に中心と半径がどのように変化するのかを的確につかめるかどうかが、得点の分かれ目になります。対策としては自分で正確に図をかくことに尽きますが、あまり時間をかけ過ぎずに、正確な図をかけるようにしておきたいところです。
　図形が他の図形の辺上を回転移動する問題で注意すべきポイントは、回転する図形に記号を書き入れること、そしておうぎ形の弧が図形の頂点を通過するようにかくことです。そのポイントさえおさえておけば、中心の移動や半径の長さ、中心角の大きさを正確につかむことができます。また、牛や羊の動ける範囲を求める問題では、特に半径の長さの変化に注意しましょう。このタイプの問題は、先の図形の回転移動のように中心、半径どちらの変化にも注意を持たなければならない問題と比べて、図形のイメージがつかみやすいです。半径の長さをつかめていれば得点のチャンスは大きく広がりますので、注意深く取り組んで確実に得点源にできるよう、図のかき方を練習しておきましょう。

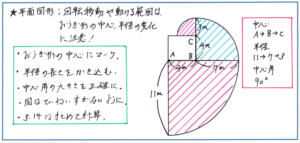
　自分で図をかいて解き進める問題で注意しておきたいのが、図をていねいにかくことにこだわり過ぎて、時間を使い過ぎないように注意することです。特に弧をかく際には、半径の長さの関係、弧が通過する点さえつかめれば、多少曲線がゆがんでしまっても構いませんので、自分が見て内容がわかる範囲での正確さでよい、という意識で問題に臨むようにしましょう。

【第2位　文章題：和と差に関する問題の総まとめはできていますか？】

　まだ「比」を演習していない5年生の7月組分けテストでは、和と差に関する問題、そして速さの問題の難度が高くなる可能性が高いです。このうち和と差に関する問題では、いくつかの要素が複合して出されることがありますので、まずは基本的な内容をしっかり固めておくようにしましょう。
　例えば、平均算では平均を求める式だけでなく「平均×個数＝全体の数」の式を確実に暗記しておくこと、2つの量の和と差がわかっていれば和差算の考え方で2量をすぐに出せることなどは、理解が曖昧になっていないか確かめておく必要があります。
　そして、2つの量の合わせた数と、それぞれの量、合計の量がわかっていれば、つるかめ算が使える、という思考の流れができているかも、テスト前に必ず確認しておきましょう。
　和差算やつるかめ算は、これからは図形や速さの問題でも使うケースが出てきます。そうした問題にもスムーズに対応できるように、「この値がわかっていれば○○算が使える」と、問題を見てすぐに解法が浮かぶようにしておくことが重要です。

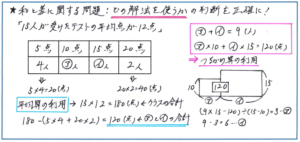
　それぞれの解法を徹底的に理解するためには図の活用も有効です。特につるかめ算では面積図を使うと2量の関係が把握しやすくなりますので、面積図のかき方もしっかりと確認しておきましょう。夏休みに演習する「濃度の問題」でも面積図を使った解き方が基本になります。これからの算数の演習で利用価値が高まって行く面積図を短い時間でかき上げられるように、この機会に練習を重ねておきましょう。

【第1位　速さの問題：線分図やダイヤグラムを使って変化の状況を把握できていますか？】

　速さの問題もまた、比を習っていない現段階では様々な要素が組み合わさった難問が出される可能性が高くあります。特にテスト終盤の応用問題として出題される場合には、長い問題文から必要な情報を選び出す、「算数ならではの問題読解力」が求められるケースがあります。こうした問題の内容を正確に把握するには国語の文章読解のように、大事な箇所に線を引くなどの方法で、解き進めるのに必要な情報を見逃さないようにすることが有効です。そのうえで、線分図やダイヤグラムにそれらの情報を書き込んで、問題で求められているポイントを視覚的にもとらえられるようにしておけば、難度が高く見える問題でも、スムーズに解き進められるようになります。
　図をかく際には、これまで演習してきた基本的内容をしっかり思い出して、それを図に反映させることを強く意識しましょう。例えばより速く動く者が折り返して、遅れて進む者と出会うといった、旅人算の折り返しのパターンでは、2者の進んだ距離の差が、折り返し地点から出会う地点までの距離の2倍になるといった基本的な内容を図から確実に導き出せれば、正解への道筋がはっきりと見えてきます。

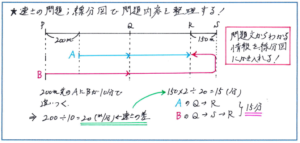
　速さの問題に限らず、長い文章で構成される問題では、小問を解き進めることで問題内容が整理されることが多くあります。つまり、比較的解きやすい(1)の答えが、次の(2)を解くヒントになる、といったケースが多いのです。そうした問題の場合、(1)を解くための情報は問題全文の中のほんの一部となる可能性が高いです。問題文が長いからといってひるむことなく、まずは(1)の問題を読んで、それから問題文に臨むと、意外にも簡単に(1)を解く情報が得られます。時間が短く感じられる組分けテストですから、着実に正解数を重ねるために、先に問題を読んでおくといったテクニックも駆使してみましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。