メールマガジン宝箱 Mail magazine

　今回の組分けテストでは、図形であれば相似と面積比、速さであればダイヤグラムと相似など、これまで習った単元が複雑に組み合わさった難問が多く出される可能性が高いです。まずはそれぞれの単元の基本的な内容を確実に理解できているかどうか確認したうえで、問題のどの部分に着眼すれば解答の方針が立てられるのかをしっかり整理しておきたいところです。そこで7月度組分けテストの対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第5位　N進法：問題を読んですぐにN進法の考え方を使う判断ができていますか？】

　N進法では、問題を読んでN進法の考え方を使うという判断がしづらいタイプの問題があります。例えば、「0、3、5の3つの数を使ってできる数を小さい方から並べると、0、3、5、30、33、35、…となります。」といった設定の問題。規則性の群数列のようにも見えますが、このような3つの数字のみで表される世界は、「3進法」の世界として考えることができます。つまり、0→0、3→1、5→2とおくことで、0、1、2で数が構成される基本的な3進法の問題として解き進めることができるのです。
　この設定のもとで、「3から数えて5番目の数は」、といった問題では基本パターンの3進法に数を置き換えて、1、2、10、11、12、21、…と数を並べると「12」に当てはまることから、それを問題の数の設定に直すと「35」と解くことができます。実際に数を並べてみても、3、5、30、33、35で同じ答えであると確かめられます。
　これが例えば40番目といった、とても並べて調べることのできない数になった場合は、下の図のようなN進法の基本解法である「3で割り続ける」解き方で進めて行きましょう。

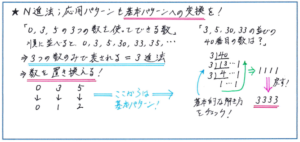
　N進法の問題は塾の演習でも他の単元と比べて解く機会が少なくなりがちですので、解き方の理解が曖昧になりがちです。組分けテストは範囲がありませんので、N進法やニュートン算といった解き方を覚えられていれば簡単で、逆にそれが少しでも曖昧になってしまうと得点のチャンスを逃してしまうような単元は、テスト前に解き方しっかりと見直しておきましょう。

【第4位　平面図形：角度の問題では二等辺三角形に注意しましょう！】

　平面図形の中でも角度を求める問題は、テスト前半の図形の小問集合として出されるケースが多く、テスト全体の得点を高めるためにも何としても得点しておきたい単元になります。
　平行線での錯角や同位角の利用、三角形の外角の性質（2つの内角の和が残りの1角の外角の大きさと等しくなる）といった基本的な考え方を使いこなすことはもちろんですが、より複雑な図形に臨む際には「二等辺三角形」の形を利用することも念頭に置いておきましょう。
　例えば下の図のような長方形に2本の対角線と1本の直線が入ったような形で考えてみましょう。角AGBの大きさを求めるにあたって、いくつかのアプローチ方法はありますが、三角形ABGの内角として考えると、角ABGに関する情報が少ないだけに難航してしまいます。そこで角AGBを三角形BCGの外角として考えてみます。角BCGは与えられた角FAGと平行線の錯角の関係にありますので、同じ大きさになり30度となります。ここで三角形BCEが二等辺三角形であることを利用すれば、角CBEも30度とわかり、それに与えられた角FBGの20度を加えることで、角CBGが50度となることがわかります。そこで外角の性質より、角BCG＋角CBG＝角AGBから角AGB＝30＋50＝80（度）と求めることができるのです。

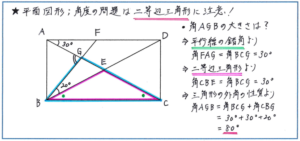
　組分けテストで出されるような角度の問題は、平行線や外角、二等辺三角形などの性質を複合的に利用して解くことを求める高いレベルにまで達する可能性があります。角度を求める方針をスムーズに立てられるように、それぞれの性質をテスト前にもう一度見直しておくようにしましょう

【第3位　濃度の問題：食塩水のやりとりを整理する図を活用できていますか？】

　食塩水の濃度の問題では、テストの後半に、食塩水をやりとりして濃度を変化させるタイプの応用問題が出される可能性が高くあります。これまでの演習で習った、単純な混ぜ合わせ（水や食塩のみを加えるパターンも含め）を面積図や天びん図で正解する流れは確実に理解を固めておく必要があります。この段階までの理解が曖昧な場合は、大至急デイリーやマンスリーで見直しを進めておきましょう。
　そのうえでやりとりの問題に正確に対応するためには、濃度や食塩水の量が変化する様子を視覚的にイメージができるようにする解法が有効です。ひとつのかたちとして、下のような長方形型の図形に、濃度・食塩の量・食塩水の量を書き込めるような図を利用する方法があります。
　この方法でやりとりの内容を記録して行くことで、変化する量が把握できることはもちろんですが、変わらない量が何かを的確に把握することができます。濃度の応用問題で正解を手にするには、変わらない量に注目することがポイントになりますので、いくつかの過程を経ても何が変わっていないのかをつかむ意識を強く持つようにしましょう。

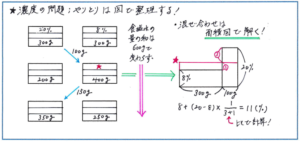
　同じくやりとりの様子を整理する手段としてビーカーの図もありますが、こちらの長方形の図であれば、数値を書き込む場所を統一でき、また変化の様子が見やすいというメリットがあります。組分けテストでは問題内容を整理するのに、あまり多くの時間をかけられません。今回ご紹介した図でもビーカー図でもどちらでも構いませんので、自分が解き進めやすい方法をテストまでに確かめて、練習を重ねておくとよいでしょう。

【第2位　平面図形：比を有効に使うための補助線の引き方はマスターできていますか？】

　平面図形では、相似や面積比といった「比」を使った問題でどれだけ得点を重ねるかが勝負の分かれ目になります。相似の基本パターンである砂時計型やピラミッド型の図形を使いこなし、高さが共通であれば底辺の長さの比が面積比になるといった面積比を正確に導き出すといった基本的な取り組みは、6年の7月組分けでは、スムーズにできることが大前提となります。これらの基本的な図形の関係の把握でつまずいてしまっている場合は、時間をかけてでも復習を重ねてください。テストではそれらを組み合わせた複雑な形が問題の対象になります。
　複雑な図形に対した際にも焦らず図形の基本的要素を活用するためには、補助線の引き方が重要になります。組分けテストにおける図形の問題で、補助線を引くことなく簡単に解き進められるケースはむしろ少ないと思っておいてください。
　有効な補助線を引くためには、自分が解いた問題を見直す際に、どのような補助線が有効であったのかを確かめることです。間違えた問題はもちろんですが、解答の根拠なしに何となく正解できてしまった問題でも、解き方を見直すようにしてください。曖昧な解き方で正解した問題をそのままにしておくと、同じような問題少しでも数値や形が変わってしまうと解けなくなってしまいます。
　また、補助線を引く際には、例えば「相似が使えそうだ」といったような先入観にとらわれないようにしましょう。例えば下の図のような問題で、正方形の辺AB上でAEとBEの長さ比が1：1とわかっているからといって、EからBCに平行な補助線を引いても、解答に時間がかかり、計算が複雑になってしまいます。ここでは面積を求める四角形BFGEを2分割する直線BGを補助線として、相似ではなく面積比の解法で進める方が速く正解に行き着けるのです。

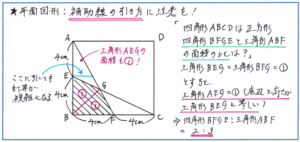
　今回ご紹介した図形はあまり複雑ではありませんが、それでも補助線の引き方ひとつで解答を進め方に大きな差が生まれてしまいます。これがより複雑な図形を扱う応用問題になると、補助線の引き方にさらにいくつかの候補が挙がってきます。その中から自分が最も解きやすい補助線を確実に引けるように、解答に直結した図形の分解方法をしっかり見直しておきましょう。

【第1位　速さの問題：ダイヤグラムと相似を使った解き方を理解できていますか？】

　速さの問題ではダイヤグラムを使って解くような、複雑な動きを題材とした難問が出される可能性が高くあります。まずはダイヤグラムを正確にかくことですが、ここでは問題文の中から必要となる情報（動く者の速さ、時間、道のりなど）を短い時間で取り出し、それをダイヤグラムに正確に書き込むことが必須になります。ここまでの作業は5年生の時にも行ってきましたが、6年生になるとそこから一歩進んで、ダイヤグラムの中から相似の関係を見つけ出して、その関係を利用して道のりや時間を解くという力が求められます。
　ポイントとなるのは平行な直線です。平面図形でも相似の基本は平行な位置関係にある直線ですが、速さを表したダイヤグラムの中に平行な直線が出てくるのは、グラフの傾きが同じ、つまり「速さが同じところ」ということになります。問題文の中から、あるいは内容を整理したダイヤグラムの中から、速さが同じ、グラフの傾きが同じ箇所には、それを強調するようなマークをするなどして、見逃さないように強調しておくとよいでしょう。
　あとは平面図形の相似の問題を解くように、比の関係（ダイヤグラムでは面積比を扱うことはほとんどありませんので相似比の関係です）を見つけ出したうえで、ダイヤグラムに書き込みをして正確に計算を進められるような設定をしましょう。

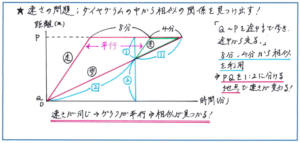
　ダイヤグラムには問題によってはいくつもの直線が交差するようなかたちで表されりものがあります。平面図形の問題を解く際のように、書き込みは雑にならないようにていねいに、見やすく行うように気をつけてください。ほんのちょっとした見間違いを防ぐことができれば、大事な応用問題での得点のチャンスが大きく広がります。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。