メールマガジン宝箱 Mail magazine

今回の内容は以下の4点です。
******************************************************************************
１、 第1回と第2回の算数入試問題がそっくり！? 学習院中等科。
２、過去問演習初期の注意点① 合格者平均点にとらわれすぎない。
３、過去問演習初期の注意点② 合格最低点をまず目標にする。
４、解答用紙から問題傾向を読み解く。
*******************************************************************************

１、 第1回と第2回の算数入試問題がそっくり！？ 学習院中等科。

多くの中学校が第1回入試、第2回入試、第3回入試・・・と複数回の受験機会を設けています。入試問題の大きな傾向は同じものの、当たり前ですが、それぞれの回では違う問題が出題されます。

そんな中、算数の入試問題で、パッと見ただけでは、同じ問題なのではないか！？と思ってしまうほど、第1回入試と第2回入試がそっくりな中学校があります。

それが、学習院中等科です。
第1回と第2回で、とてもよく似た問題が出題されています。

第1回と第2回の問題レベルは同程度で、問題数も同じです。
毎年大問1が計算問題、大問2が小問集合、大問3から大問6までが応用問題という問題構成も第1回、第2回で同じです。

問題の類似ですが、まず大問2の小問集合は完全に同じ単元から出題されます。2022年度は第1回、第2回ともに(1)が植木算、(2)が集合、(3)が通過算、(4)が数の性質からの出題でした。問題の内容が同じで、求める内容が異なる（第1回が速さを求めるのに対し、第2回は距離を求める、など）だけのものがほとんどで、中には数値を換えただけの問題もあります。2022年度は(2)と(4)が数値換えの問題でした。

大問3以降の応用問題も単元が同じで、解き方も全く同じ場合もあります。例えば2022年度は第1回、第2回とも大問3が平面図形から「動ける範囲」の問題、大問4が規則性から「分数の数列」、大問5が速さとグラフ、大問6がトーナメント表を使った条件整理の問題、といった内容で共通していました。

このうち、大問3の図形問題は、糸の先端を図形に付ける問題ですが、第1回の図形が三角形であるのに対し、第2回が四角形というだけの違いで、計算の進め方は全く同じです。
それ以外の応用問題は、題材は同じですが、例えば大問5の速さとグラフの問題では、動き方が異なるためグラフの形状が異なり、解き方も第1回では別のグラフを自分でかいて解く（同校の特徴的な傾向のひとつです）のに対し、第2回は問題のグラフのみで解く、といった違いがあります。

それでも同じ単元からの出題になりますので、第1回入試を受けた受験生は第2回入試でかなり有利になります。

ただ、過去5年間では2020年度と2021年度で、応用問題4題のうち1題は全く異なる単元からの出題が見られました。必ず毎年、全ての問題が同じ単元から出されるとは言い切れませんが、それでもとても類似した問題が出されるという学習院中等科の特徴は変わらず見られています。

中学受験算数に詳しい方々からすると、第1回と第2回の入試問題がそっくり、と聞かれてまず浮かぶのは攻玉社中学ではないでしょうか。

確かに攻玉社と言えば、第1回と第2回の入試問題がよく似ている学校の筆頭に挙がる学校で、2018年度まではまさにそっくりの出題でした。単元が同じなだけではなく、特徴的な図形や表が数値換えで出され、ほとんど同じ解き方で対応できる問題がテストの大半を占めていたのです。小問集合も同じ単元からの出題が目立っていました。

それが2019年度には応用問題で類似した問題の数が減り、2020年度以降はさらに類似する問題が減っています。大問1の約束記号の問題が第1回、第2回ともに出題されていますが、小問集合については同じ単元からの出題がなくなりました。応用問題である大問3と大問4も、単元こそ同じですが、かつてほどの類似性はなくなったのです

例えば2022年度であれば、第1回、第2回とも、大問3が3人の動きを読み取る旅人算で、自分でグラフをかき、そこから比を使って解くところまでは同じですが、3人の動き方が第1回と第2回で異なります。第4問も立体図形で「すい体」を題材に、切断をからめる点は共通していますが、細かな設定や図形の成り立ちは共通していません。

このように、かつての攻玉社らしさが2019年度以降は見られなくなっていますが、それでも、同じ単元からの出題であることには変わりなく、同じような解法で解く問題が含まれることもありますので、第1回入試を受験した方が、第2回入試のみを受験するよりも有利であると言えます。

これらは、出来るだけ多く第一志望の生徒さんに合格して欲しいという中学校の思いの表れでしょう。また、志望校対策をしっかりやってきた子、複数回受験してくれた子がより報われやすいようにしたいという思いが強いのではないでしょうか。

上記の中学校は、第1回と第2回入試がそっくりというとても特徴的な学校ですが、過去問を見ていると各学校とも様々な傾向があることに気づきます。

どの中学校も大きな入試傾向というのは毎年ほとんど変わりませんので、志望校合格に向けては、過去問演習がとても大切なのです。

そこで今回は過去問への取り組みが本格的にスタートするこの時期に意識して頂きたいことについてもご説明させて頂きます。

２、過去問演習の初期の注意点① 合格者平均にとらわれすぎない。

過去問集（声の教育社のものを例にお話致します）に収録されている「入試結果表」には、各年度・各回の数値データが掲載されています。慶應3校など点数が非公表になっている場合を除いては、科目ごとに配点、合格者平均点、受験者平均点といった数値が示されています。最初はどうしても、余裕をもって合格したい、合格を確実なものにしたいという思いから、合格者平均点に注目しすぎてしまうのですが、合格者平均点は言葉の通り、合格した受験生の平均点ですので、特に最難関校の併願校になるような学校では、トップレベルの受験生が高得点を取り、合格者平均点を上げていますので、合格者平均点は必ずしもその学校に合格するためにクリアーすべき基準点とは言えません。合格者平均だけにとらわれることがないようにしましょう。

３、過去問演習の初期の注意点② 合格最低点をまず目標にする。

まず注目すべきは合格者最低点です。合格者最低点を超えていれば、その回の受験では合格することになりますので、合格平均点よりも、まずはこの合格最低点を目標にしましょう。　　

ただ、合格者最低点は4科目の合計で表示されていますので、各科目の合格者最低点は4科目全体と該当する科目の割合で換算するとよいでしょう。例えば、算国が120点満点、理科社会が80点満点の合計400点満点のテストの場合で、合格者最低点が6割の240点だったとすると、算数と国語の合格者最低点は240×120/400（400分の120）＝72点となります。理社の合格者最低点はそれぞれ、240×80/400（400分の80）＝48点です。　　　　

４、 解答用紙から問題傾向を読み解く

解答用紙を眺めるだけで、答えのみを書かせる学校なのか、記述問題が多いのか、ということがすぐにわかります。算数で途中式を書かせる学校などは慣れが必要ですので、解答用紙を実物大に拡大コピーして練習しましょう。また、解答用紙には推定配点（学校配点の場合もあります）が記載されています。以下の写真のように解答用紙をコピーして配点を書き込んでみましょう。どの問題とどの問題を取れれば合格最低点を突破できるのか、得点戦略がぐっと考えやすくなります。

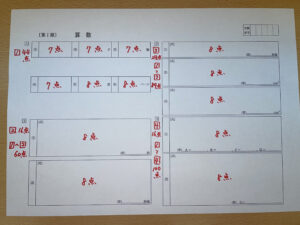
いよいよ過去問の季節が始まります。充実した過去問演習をスタートしましょう！