メールマガジン宝箱 Mail magazine

　今回の5年生第5回組分けは、範囲のないテストとなります。その中でも特に注意すべきは、夏期講習で学習した「比の基本」「相似」「面積比」といった比に関する単元です。中学受験算数の最重要単元「比」については、後期から本格的に取り組むことになりますが、そこで中学受験の算数は一気にレベルアップしたステージに進みます。まずは夏期講習で習った「比」の基本範囲を確実に理解しておきましょう。今回の組分けテスト対策を通して、比に関する基本範囲をマスターして、後期からの学習への備えを万全にしておきたいところです。そこで「比」の単元をはじめ、第5回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

【第1位　面積比・相似：図形の中に共通する部分を正確に見つけられていますか？】

　面積比・相似といった「図形と比」の単元では、相似の関係や面積比を正確に求めるために、図形どうしの「共通する部分」をスピーディーに見つける視点が必要となります。相似では、クロス型やピラミッド型といった基本形では相似比は簡単に求められても、下の図のように向きが異なる図形どうしになると、どの辺とどの辺が対応するかで迷ってしまうことはないでしょうか。そこで図のように、共通する角度に同じ記号を書きこんでおくと、●→○のように記号をつなぐことで、対応する辺が見つけやすくなります。
　また面積比の問題では、平行四辺形や長方形の中に含まれる三角形の面積比を求める問題がありますが、「高さが共通の三角形の面積比は底辺の長さの比」という原則にとらわれ過ぎて、「高さ」に注目しようとしても、実際には高さを表す線が図形内に見られるケースはほとんどありません。そのような場合は、高さではなく、底辺に対する「頂点」が共通していることに着目すれば、底辺の長さの比を断然求めやすくなります。この頂点に着目する習慣が身に着けば、これから演習する面積比の問題がスムーズに解けるようになります。

　相似・面積比の問題は慣れが必要と言われますが、そのためには、様々なパターンの図形の問題で、「共通する部分」にスピーディーに着目する姿勢が大前提となります。相似での角度の記号のように、書き込みをすることも効果的ですので、自分の手を使って解く練習を多く積み重ねてください。

【第2位　食塩水の濃度・売買損益：「変わらない量」に注目して式を立てられていますか？】

　「食塩水の濃度」の問題では、5年の後期以降、混ぜ合わせなど難度の高い問題に対して、主に面積図を使って解くケースがどんどん出てきます。まずはその前段階として、食塩水に水を加えたり、食塩を加えたりする基本タイプの問題に対して、「変わらない量」に着目することでスムーズに式が立てられているかをチェックしておきましょう。例えば「40%の食塩水500gから100gの食塩水を取り出して、かわりに100gの水を入れて、よくかきまぜました。これによってできた食塩水の濃さは何%ですか」と言った問題。順を追って式を立てれば決して難しい問題ではないのですが、このタイプの問題はテストの序盤で出題される正解必須の問題であり、かつスピーディーに解答することが求められます。100gの食塩水を取り出した時点で「濃度」が変わらず。水を加えても「食塩の量」が変わらないことを瞬時に把握して、式を立てるようにしましょう。
　「売買損益」では価格の設定が2段階以上になる問題での対応が重要になります。例えば「ある商品を仕入れ値の2割増しで定価としましたが、売れなかったので定価の15%引きで売ったところ、200円の利益がありました。この商品の仕入れ値はいくらですか。」といった問題では、定価が変動してしまうので、変わらない仕入れ値を1または100と置いて式を立てれば正解に行き着くことができますが、状況をより明確にイメージするためには、下のような線分図をかいてもよいでしょう。

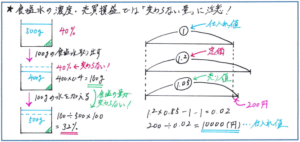
　「食塩水の濃度」も「売買損益」も今回ご紹介したようなシンプルな問題であれば無理に図をかく必要はありませんが、式の立て方で迷うような場合は、テスト前の練習の段階で図をかいて解く作業を積み重ねておくとよいでしょう。

【第3位　通過算・流水算：図をフル活用することがスピーディーに正解するポイントです！】

　速さの問題の中でも「通過算」「流水算」では、問題内容を図で整理できるかどうかが、速く正確に解答に行き着くための分かれ目になります。
　通過算では、列車どうしが追いつき追い越される場面、すれ違う場面を図にすることで、「列車の長さの和を速さの和（または差）で割って時間を求める」という原則を視覚的にもイメージできます。その際に『予習シリーズ』の図にもありますように、例えば列車が別の列車を追い起こす場合には、「追い越す列車の先頭を○、最後尾を●、追い越される列車の最後尾を○、先頭を●として、○が一致する時点から●が一致する時点までの時間を求める」とすることで、列車の長さをどのようにとらえればよいのかがスムーズに理解できます。すれ違う場合には、両方の列車の先頭を○、最後尾を●とすれば同じように長さをとらえやすくなります。また、列車や鉄橋をかく際には、あくまでシンプルに、単純な四角で表して、列車の窓や車輪までかき込むことは避けましょう。時間がかかる上に、図が複雑になって、より見えづらくなってしまいます。
　流水算では、「上り」「下り」の動きを把握しやすくするために、「斜めの線分図」を利用する方法があります。坂道のように線分図を斜めにかき、川の上流と下流の位置を示すことで、上りの速さと下りの速さの関係を視覚的にとらえることができるようになるのです。流水算は今後、船の出会い算や、船が故障して流される、といった様々な出題パターンが出てきます。さらにそれらのパターンをグラフとの関連で解き進めなくてはならなくなります。まだ基本的な問題を扱う今のうちから、上り・下りの船の動きを正確に把握するための有効な図のかき方を身につけておきましょう。

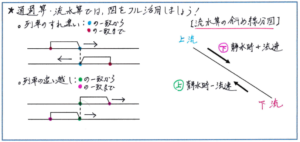
　通過算・流水算ともに様々なパターンの問題に慣れてくれば、必ずしも図を活用しなくても正解に行き着くことができますが、頭の中で正確なイメージを固められているかどうかで、問題の正答率が大きく変わってきます。そのためにも、今のうちに図をかいて解く習慣をしっかり身につけておきましょう。

【第4位　水深の変化：立体を真正面から見た平面で考える習慣が身についていますか？】

　立体図形の「水深の変化」の問題で、水を入れる水そうの形が「腰かけの浴槽の形」や「仕切りが入った形」と複雑になってくると、問題を見た瞬間に「難しそう」というイメージにとらわれて、問題を解く初動が遅れてしまうことはないでしょうか。確かにこのタイプの問題では「段階を分けて解く」という作業が必要なうえ、グラフとの関連にも着目しなくてはならない点で難度は高くなります。それでも、問題内容を解きほぐす図を使った解法で進めれば、水深変化の状況が一気に把握しやすくなります。その図とは、水そうを真正面から見た「断面図」のような平面のことです。このタイプの問題に出てくる水そうの形は、段差がついたり、仕切りが入ったりと複雑になっても、「奥行きの長さ」は一定であるケースがほとんどです。そこで、一定の奥行きの長さで立体の体積を割って求められる平面で考えることができるのです。
　下の図のように、平面を「区分け」することで、平面の中で起こる変化を水深の変化につなげて考えることができます。さらにはグラフの変化と「区分け」された平面の関係を把握することで、水深の変化とグラフの関係も正確につかむことができるのです。

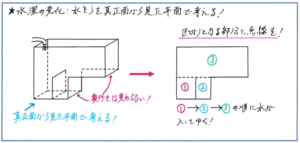
　このタイプの問題は組分けテストでも後半に出題されるケースが多く、大問すべてを得点できなくても、(1)(2)で出題されるような立体の成り立ちを理解すれば解ける問題で正解できるだけでも、テスト全体の得点を大きくアップさせることができます。そのためには、立体を立体のまま考えるのではなく、平面に変換させることが立体の成り立ちを理解するための重要なステップとなります。また入試でもこのタイプの問題は頻出ですので、図をかいて解く流れをしっかりつかんでおきましょう。

【第5位　点の移動：面積の変化を「場面分け」して考えられていますか？】

　平面図形の中で「点の移動」の問題は、【第4位】の「水深の変化」と同じく、時間の経過とともに起こる変化を正確に把握することがポイントとなります。この「点の移動」の問題も、夏休み明けの5年後期以降は、図形が複雑な形になったり、移動する点の数が増えるなど、難度が急激にアップしてきます。そうした問題への対応力をつけるために、まずはシンプルな形を題材として、点の動きによる面積の変化を「場面分け」してつかむ練習をしておきましょう。その際に、グラフとの関係についての理解度を必ずチェックしておくようにしてください。このタイプの問題では、点が動く時間と面積の変化の関係を表したグラフがセットで出されるケースがほとんどです。
　例えば下のような長方形の辺上を点が動いた際の三角形の面積の変化を題材とした問題。点が長方形の頂点を通るごとに、面積の変化の状況は変わってきます。その状況の変化を「場面分け」として、ひとつひとつ確実につかむことが大前提となります。
　そのうえで、このタイプの問題で多く出される、「三角形の面積が2回目に三角形ABCの面積の3分の1になるのは何秒後ですか」といった内容に対応するには、グラフをもとに考える解法が有効です。相似の考え方に慣れれば、グラフの中に三角形を見つけて解き進めることもできますが、相似を習って間もない今の段階では難しいかと思われます。そこで、グラフから三角形PBCの面積が「1秒間に何平方cm増える（減る）か」を導き出して、それをもとに計算で解き進めればよいでしょう。

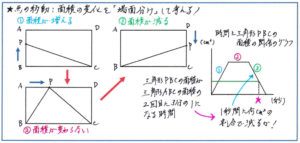
　出題の内容に関わらず、まずは面積の変化を正確に把握することが、このタイプの問題を解く際の大原則です。ここでも頭の中だけで解き進めようとすると、思わぬところでミスが発生してしまいます。場面分けした図形を自分の手で、簡単な形で構いませんのでかき出すことで、面積の変化を正確にイメージできるようになります。手を使うことを惜しまず図を活用する習慣を身につけておくことが、今回の組分けテストだけでなく、後期からの学習にも大きな効果をもたらします。ぜひ自分で図をかく作業を積極的に行うようにしてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。