メールマガジン宝箱 Mail magazine

　新6年生になって最初の組分けテストです。今よりも上位のクラスにジャンプアップできる大チャンスですが、これまでに習った単元すべてが出題対象になるため、どこから復習を進めればよいのかを見定めるのがとても難しくなります。さらに、6年生になったばかりで、新たなカリキュラムに慣れるだけでも大変な時期にあり、重要単元でどこまで理解が固められているか、できるだけ時間をかけずにしっかりと確かめておきたいところです。そこで新6年3月度組分けテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形：相似と面積比を的確に使い分けられていますか？】

　平面図形の問題では、1つの図形の中から、「相似」と「高さ共通の図形での面積比は底面比と等しい」という2つの要素を的確に見つけ出して、解答のために使いこなせるかどうかがポイントになります。例えば下の図で、「台形ＡＢＣＤの辺ＡＤと辺ＢＣが平行で、辺ＡＤの長さと辺ＢＣの長さの比が2：5のとき、三角形ＣＤＥの面積は台形ＡＢＣＤの面積の何倍ですか」といった問題にはどのように対応すればよいでしょうか。
　まずは辺ＡＤと辺ＢＣが平行であることから、三角形ＡＤＥと三角形ＣＢＥが相似であることを瞬時に判断して、図に比の値をかき込みます。次に三角形ＡＣＤに着目すると、三角形ＡＤＥと三角形ＣＤＥは高さが共通な三角形で、ＡＥ：ＣＥ＝2：5（三角形ＡＤＥと三角形ＣＢＥの相似比が2：5のため）であるため、三角形ＡＤＥの面積と三角形ＣＤＥの面積が2：5になります。また、三角形ＡＢＣと三角形ＡＣＤも高さが同じなため、面積比はＡＤ：ＢＣの2：5となります。以上より、三角形ＡＣＤの面積は台形ＡＢＣＤの面積の2/7倍となり、三角形ＣＤＥの面積は三角形ＡＣＤの面積の5/7倍であることから、三角形ＣＤＥの面積は台形ＡＢＣＤの面積の、2/7×5/7＝10/49（倍）と求めることができます。

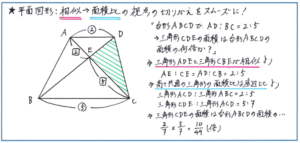
　新6年になると、相似と面積比を組み合わせた問題が多く出されるようになります。今回の問題にあったような典型的な相似のパターンを頭の中にしっかりインプットしておけば、図形の中から相似の関係にある図形を見つけ出すことに大きな負担はないでしょう。重要なのは、そこから高さの等しい三角形の面積比の関係へと視点をスムーズに移行させることです。まずは相似の典型的なパターンを確実に覚え込んだうえで、比の関係が視覚的につかめるように、図に比の値をかき込むという流れをテストの際に行えるように、くり返し練習をしておきましょう。

【第2位　速さと比：速さの比と時間の比の逆比関係を使いこなせていますか？】

　速さの問題で、「距離が同じ場合は、速さの比と時間の比が逆比」という関係を使う問題は、これまで何度も解いてきました。この関係は今後も使うケースが多くあり、様々なパターンで出題されるようになります。これまでのような、問題を見てすぐに逆比を使うと着想できるようなレベルではなく、長い文章から逆比の関係を使うことを気づかせたり、グラフの中で逆比を使わせるなど、難度がアップしたかたちになるため、考え方をしっかり固めておく必要があります。
　例えば「Ｐ地点からＱ地点まで、Ａ君は一定の速さで進み、Ｂ君は途中のＲ地点で速さを変えて進みます。Ｐ地点からＲ地点まではＡ君の方がＢ君より毎分10m速く、Ｒ地点からＱ地点まではＢ君の方がＡ君よりも毎分20m速く進みます。Ａ君とＢ君は同時にＰ地点を出発して、30分後に2人同時にＱ地点に到着しました。Ｂ君が速さを変えたのは、Ｐ地点を出発してから何分後ですか」といった問題。
　この問題を、グラフを使って解いてみましょう。下のように、Ａ君がＰ地点からＱ地点まで進む様子は一直線に、Ｂ君はＲ地点で速さが変化するため、折線のかたちになります。2人が同時にＰ地点を出発して、30分後に同時にＱ地点に着くので、Ｐ地点とＱ地点で2人の動きを表すグラフは重なります。
　ここで、Ｂ君がＲ地点に着いた時点での2人の間の距離（★）は、Ｂ君がＰ地点からＲ地点に進むまでに「毎分10mの割合で開く」2人の間の距離であり、またＢ君がＲ地点からＱ地点に進むまでに「毎分20mの割合で狭まる」2人の間の距離でもあります。ここに、「距離が同じ場合は、速さの比と時間の比が逆比」の関係が成り立ち、Ｐ地点からＲ地点までにかかった時間と、Ｒ地点からＱ地点までにかかった時間の比が、速さの差の比の10：20＝1：2の逆比である2：1となります。よって、Ｂ君が速さを変えたのは、30×2/(2＋1)＝20（分後）と求められます。

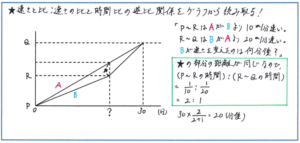
　問題内容をグラフで表すという作業は、手間と時間がかかるために避けてしまいがちですが、動きを視覚的にとらえる効果だけでなく、比の関係も断然把握しやすくなります。特に、速さと時間の逆比の関係をグラフからつかめるようになると、難問を解く力が一気にアップします。面倒に見える作業にチャレンジすることで、問題を解くスピードが大きく上がることをぜひ体感してください。

【第3位　立体図形：(底面積の比)×(高さの比)＝(体積の比)の関係を使いこなしましょう！】

　テスト全体の中で、比を使って解く問題の占める割合がどんどん高くなる中で、立体図形でも比を用いるケースが増えてきます。互いに相似の関係にある立体で、相似比がa：bのとき、体積が、(a×a×a)：(b×b×b)となるといった基本パターンはもちろん、体積の公式である[底面積×高さ＝体積]を利用して、(底面積の比)×(高さの比)＝(体積の比)となることを利用した解き方にもスムーズに対応できるようにしておく必要があります。
　例えば「底面の半径の長さが4cmの円柱Ａと、底面の半径の長さが6cmの円柱Ｂの体積の比が28：45のとき、2つの円柱の高さの比を最も簡単な整数の比で求めなさい」といった問題では、体積比が28：45であることから、仮に円柱Ａの体積を280立方cm、円柱Ｂの体積を450立方cmとおいても、3.14が計算に含まれるため、高さを求める仮の計算がとても複雑になってしまいます。そこで、底面積の比が(4×4)：(6×6)＝16：36＝4：9であることから、(底面積の比)×(高さの比)＝(体積の比)を利用すれば、高さの比を、28/4：45/9＝7：5と求めることができるのです。

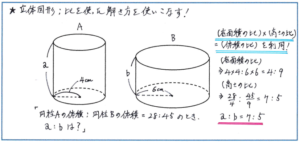
　この解き方をしっかり身につけておけば、複雑な計算をすることなしに正解に行き着くことができます。もちろん、冒頭に挙げた相似比から求められる体積比を使って解く問題、そして表面積で、相似比から求められる面積比を使って解く問題も出題される可能性は高くありますので、まずは基本をしっかりおさえて、比を使って立体図形の問題を解く方法に慣れておきましょう。

【第4位　場合の数：あてはまらないケースを確実に選び出せていますか？】

　場合の数の問題を解く際に注意して頂きたいのが、「あてはまらないケースを確実に除外すること」です。6年生のテストとなると、単純にあてはまるケースを選び出すだけでなく、問題内容を正確に読み込んで、どのような場合に条件に合わないケースとなるのかをおさえて解き進める力も求められます。例えば、「サイコロを何回か振って、出た目の数だけ時計回りにコマを進めるゲームをします。コマはＡから出発して、Ａにちょうどつくとゴールとなってゲーム終了です。サイコロを2回振ってコマを進めた時点で、Ｃにコマがあるとき、1回目と2回目のサイコロの目の出方として考えられるものは全部で何通りありますか」といった、すごろくタイプの問題では、どこに注意して解き進めればよいでしょうか。
　Ａからスタートして、サイコロを2回振ってＣにコマがあるのは、サイコロの目の数2回分の合計が、2か7か12になるときです。目の数の合計が2になるのはコマの出方が（1、1）のときのみ、12になるのは（6、6）になるときのみです。ポイントは出た目の数の合計が7になるときで、数の合計だけを考えれば、（1、6）（2、5）（3、4）（4、3）（5、2）（6、1）の6通りありますが、このうち（5、2）は1回目のサイコロの目が5となり、Ａにコマがついてゲーム終了となってしまいますので、除かなくてはなりません。よって、あてはまるケースは全部で7通りとなります。

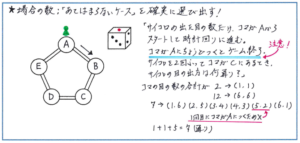
　この問題のようにサイコロの目を使った問題では、使える数が1から6までの整数という大前提がありますが、これからのSAPIXのテストでは、さらに一歩踏み込んだ条件が含まれるケースが圧倒的に多くなります。この条件の読み取りが難しい点が、場合の数の問題の難度を大きく上げる要素になりますが、まずはじっくり問題文を読んで条件を整理する意識を持つこと、そして何より、解いた問題を見直す中で自分がどの条件を見逃してしまっていたのかを、必ずチェックしておくようにしましょう。そうした地道な見直し作業の積み重ねが、場合の数だけでなく、速さなどでも見られる複雑な設定の問題を攻略する力を養います。

【第5位　比と割合の問題：逆比と連比を問題内容に合わせて使いこなせていますか？】

　比と割合の問題でも場合の数の問題と同じく、問題文が長く、条件が複雑に設定されるケースが多くなります。そこで、逆比、連比をいかにスピーディーな判断のもとで効果的に使えるかで、難度の高い問題での得点力が大きく変わってきます。
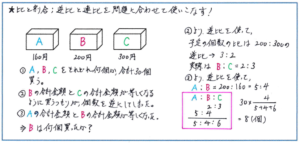
　例えば、「1個あたりの値段が、160円の商品Ａ、200円の商品Ｂ、300円の商品Ｂの3種類を組み合わせてそれぞれ何個か、合計で30個買いました。商品Ｂの合計金額と商品Ｃの合計金額が等しくなるように買うつもりが、商品Ｂと商品Ｃの個数を逆にして買ってしまったので、商品Ａの合計金額と商品Ｂの合計金額が等しくなりました。このとき、商品Ｂは何個買いましたか」といった問題はどのように解き進めればよいでしょうか。
　問題文も長く、複雑に見えますが、解き方の道筋さえしっかり見つけられれば、苦もなく正解に行き着くことができます。まず、合計金額がわかっておらず、全体の個数がわかっていて、そこから商品Ｂの個数を求めるという問題内容から、商品Ａ、商品Ｂ、商品Ｃの個数の比が連比でわかれば、正解に大きく近づくことがわかります。そこから、商品Ｂと商品Ｃの個数の比、商品Ａと商品Ｂの個数の比それぞれがわかればよい、とさかのぼって考えることが大事になります。ここで、「合計金額が等しくなるように」という点に注目すれば、合計金額が等しい場合には、個数の比は単価の比の逆比というポイントに行き着くことができます。これより、商品Ｂの個数：商品Ｃの個数は、200：300＝2：3の逆比の3：2の予定が逆になったので、実際には2：3、商品Ａの個数：商品Ｂの個数は、160：200＝4：5の逆比の5：4とわかります。これより連比の解き方で、商品Ａの個数：商品Ｂの個数：商品Ｃの個数＝5：4：6となることから、商品Ｂの個数は、30÷(5＋4＋6)×4＝8（個）より、8個と求められます。

　今回ご紹介しましたような複雑に見える問題でも、逆比、連比の基本的な使い方をしっかり習得していれば、解答までの道筋がハッキリと見えるようになり、それは今後の算数の問題に臨むうえで大きな自信を手にすることにつながります。特に逆比は【第2位】でご紹介した速さの問題など、多くの問題で大いに効果を発揮します。どのような場合に逆比を活用できるのかを意識しながら解き進めるようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。