メールマガジン宝箱 Mail magazine

　7月度組分けテストは、前期の総仕上げとして、現段階での算数の習熟度をチェックし、本格的な志望校対策に取り組むための足場づくりができているかを確かめる大事なテストとなります。基本から応用まで、じっくりと単元ごとの理解度を確かめたいところですが、7月組分けの対策にあてられる時間は限られています。

　そこで、これまで培ってきた解法が定着できているかどうかチェック頂けるように、6年7月度組分けテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形（相似と面積比）：相似の利用、比のそろえ方といった解法は定着できていますか？】

　平面図形では、相似、面積比を組み合わせた標準以上の難度の問題がテストの後半に出されるケースが多くあります。特に面積比を求める際に、図形の中にある相似の関係を利用し、さらに異なる比をそろえるといった解法の流れを的確に使いこなす力が試されるため、それぞれの解法の理解を確実にしておく必要があります。

　例えば下の図のような長方形ABCDの中に引いた2本の直線によってできる三角形CDPの面積が、長方形ABCDの面積の何倍かを求める問題。三角形CDPを含む三角形DCF（または三角形CDE）がありますので、この三角形DCFが長方形ABCDの面積の何倍かを求め、そこから三角形CDPが三角形DCFの何倍かがわかれば、スムーズに正解に行き着くことができます。

　三角形DCFの面積については、さらにそれを含む三角形BCDの面積が長方形ABCDの面積の1/2であることを利用、そこから面積比＝底辺の長さの比を利用して、三角形DCFの面積が三角形BCDの面積の2/3倍であることがわかりますので、三角形DCFの面積が長方形ABCDの面積の、1/2×2/3（倍）と求められます。ここで1/2×2/3＝1/3と計算をしてしまっても構わないのですが、さらにこの後に分数のかけ算が続くことがわかっていますので、最後にまとめて約分計算をすべく、式のままに残しておくことも有効です。

　あとは三角形CDPの面積と三角形DCFの面積の関係ですが、DP：FPの比がわかれば、ここでもまた、面積比＝底辺の長さの比を利用することができます。DP：FPについては、三角形DEPと三角形FCPが相似となるため、その相似比として求めることができます。この相似の関係は典型的な砂時計型ですので、瞬時に把握できなくてはいけません。2つの三角形で長さがわかっているのは、DEとFCで、DEについてはAE：DE＝1：3、FCについてはBF：FC＝1：2となり、AD＝BC（長方形の対辺）より、AD、BCの長さを(1＋3＝)4と、(1＋2＝)3の最小公倍数12にそろえると、DEが12×3/4＝9、FCが12×2/3＝8より、三角形DEPと三角形FCPの相似比が9：8と求められます。

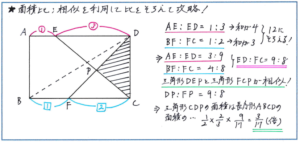
　これで解答の材料がそろいました。三角形CDPの面積は、三角形DCFの面積の9/17倍となるため、長方形ABCDの、1/2×2/3×9/17＝3/17（倍）と求めることができます。

　平面図形の問題を攻略するためには、今回ご紹介したような解法の組み合わせを駆使できるように、各解法の使い方を徹底しておきましょう。過去のマンスリーを見直して、理解が曖昧な解法をチェックしておくとよいでしょう。

【第2位　速さの問題：「相似」を使ってグラフを読み取ることができていますか？】

　速さの問題では、速さが変わる、往復するといった複雑な動きが含まれる難問が出される可能性が高くります。そこで、グラフを的確に使えれば、解答方針が圧倒的に立てやすくなります。まずはグラフを正確にかくことが重要ですが、そのためには問題文の中から必要となる情報（動く者の速さ、時間、道のりなど）を短い時間でピックアップして、それをグラフに正確に書き込むことが必須になります。さらに、グラフの中から相似の関係を見つけ出して、その関係を利用して道のりや時間を解くという力が求められます。

　ポイントとなるのはグラフの中にある平行な直線を見出すことです。平面図形でも相似の基本は平行な位置関係にある直線ですが、速さを表したグラフの中に平行な直線が出てくるのは、グラフの傾きが同じ、つまり「速さが同じところ」ということになります。問題文の中から、あるいは問題内容を整理したグラフの中から、速さが同じ、グラフの傾きが同じ箇所には、それを強調するようなマークをするなどして、見逃さないようにしておくとよいでしょう。

　例えば下のような、QからPまでを「走って進む場合」「歩いて進む場合」「途中まで歩いてそこから走って進む場合」がグラフで表された場合、「走った」部分のグラフが平行になります。

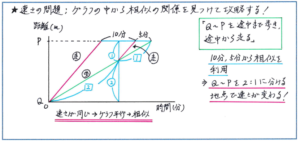
　あとは平面図形の相似の問題を解くように、比の関係（グラフでは面積比を扱うことはほとんどありませんので相似比の関係です）を見つけ出したうえで、グラフに書き込みをすれば、どの地点で速さが変わったのかを求められます。

　問題によってはいくつもの直線が交差するようなかたちでグラフが表されるものがあります。平面図形の問題を解く際のように、書き込みは雑にならないようにていねいに、見やすく行うように気をつけてください。ほんのちょっとした見間違いを防ぐことができれば、大事な応用問題での得点のチャンスが大きく広がります。

【第3位　割合と比：問題内容を整理する線分図を正確にかけていますか？】

　割合と比の単元からは、様々なタイプの問題が出題されます。どのような問題であってもそれを攻略するためには、図をかいて内容を整理することが重要となります。例えば次のような問題にはどのように対応すればよいでしょうか。
「ある仕事を春子さんが6時間したあとに、秋子さんが5時間するとちょうど終えることができます。また、この仕事は春子さんが3時間したあとに、秋子さんが10時間してもちょうど終えることができます。このとき、春子さんと秋子さんが1時間でできる仕事量の比を最も簡単な整数の比で答えなさい。」

　問題としてはテスト前半に出されるタイプのものですが、それだけに失点は何としても防がなくてはなりません。しかも後半の問題にかける時間を考えると、少しでも短時間で正解まで行き着くことが必須となります。

　仕事の進め方が2つのパターンで示されています。春子さんと秋子さんのうちどちらかの仕事した時間が同じであれば容易に解けるものですが、2人ともに時間が異なるために問題内容が複雑に感じられます。このような場合も下のように線分図を用いて内容を整理すると、対応しやすくなります。

　仕事量全体を表す線分を2本、上を「春子さん6時間＋秋子さん5時間」のケース、下を「春子さん3時間＋秋子さん10時間」のケースとします。そして、春子さんの1時間の仕事量をマル1、秋子さんの1時間の仕事量をシカク1とします。上の線は、「マル6＋シカク5」、下の線が「マル3＋シカク10で」と表すことができます（メルマガではマル→赤、シカク→青としてあります）。

　そこで上下の線分図を見比べることで、マル6－マル3＝マル3の長さが、シカク10－シカク5＝シカク5の長さと同じになることがわかります。ここでマル3＝シカク5より桜子さんが3時間でできる仕事量と桃子さんが5時間でできる仕事量が等しいことから、2人が1時間でできる仕事量の比は(1÷3)：(1÷5)＝5：3と求めることができるのです。

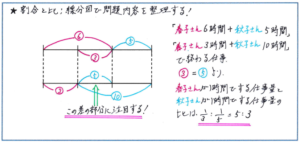
　慣れてくれば、線分図をかかなくても、例えば「春子×6＋秋子×5」という式と、「春子×3＋秋子×10」という式をたてに並べ書いて、春子×3＝秋子×5とすることもできますが、まずは図をしっかりかいて、視覚的イメージを固めたうえで内容を整理することが大切です。線分図をかく時間を余計に感じられるかもしれませんが、問題をスムーズに解くには解答方針が必要で、その方針を速く正確に立てるためには線分図が有効となります。

【第4位　規則性に関する問題：問題内容に合わせた的確な書き出しができていますか？】

　規則性の単元からも、数列、図形の規則性など様々な問題が出されると考えられますが、群数列に関する問題では、規則をつかむために有効な書き出しが必要となります。例えば次のような問題。

　　「長い紙テープを、10、10、20、10、20、30、10、20、30、40、10、…（単位はすべてcmです）と、ある規則にしたがって左から切っていきます。例えば、20cmのテープを3本切り取るには、8回切る必要があります。このとき、60cmのテープを2本切り取るには、何回切る必要がありますか。」
　
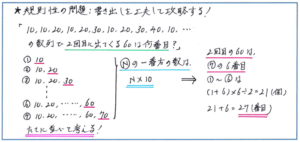
　この数の並び方が、左から「10」「10、20」「10、20、30」と、ひとつずつグループに含まれる数が増えて行くような群数列であることはすぐに把握できるでしょう。ポイントはここで、数列のグループが変わるところに「／」を入れるだけでは解答への道筋が見えづらく、違ったかたちの書き出しが必要になるという点です。

　数列の1番目のグループを「10」、2番目を「10、20」、3番目を「10、20、30」、…としたうえで、見やすくなるように、各グループの1番はじめの数である10がたてにそろうように、グループごとにたてにかき並べてみます。すると、1番目→10、2番目→20、3番目→30と、「グループを表す数を10倍した数が、グループの最後の数として右端にくること」がわかります。これにより、60が最初に出てくるのが6番目のグループの最後、2回目に出てくるのが7番目のグループの6番目となります。

　そこで、60cmのテープを2本切り取るための回数は、6番目のグループの最後の数までにある数の個数の和に、7番目のグループの6を加えることで求められます。各グループに含まれる数の個数は1番目に1個、2番目に2個、…となりますので、6番目の最後までの個数の和は、(1＋6)×6÷2＝21、よって21＋6＝27より、テープを27回切る必要があると求められます。

　規則性の問題では、与えられた数列に書き込みをすることで解決できるものもありますが、今回の問題のように、さらにもう一工夫を加えた書き出しが有効にあるケースがあります。内容を整理しやすいかたちで書き出しをすることで規則を確実に把握し、式を立てられるように練習を重ねましょう。

【第5位　立体図形（水深変化）：「もしもおもりの高さよりも…」の考え方を使えていますか？】

　立体図形の中で、水の入った容器の中におもりを入れた際の水の深さについて考えさせる問題があります。もちろん大前提となるのは、「沈めたおもりの体積の分だけ水面が上がる」という考え方で、断面図を用いて水面の高さを確認するという解法が鉄則となります。

　ここで注意しておきたいのが、上がった水面の高さとおもりの高さの関係です。例えば、容器に入れるおもりの高さが容器よりも高い場合であれば、水面の高さは必ずおもりの高さよりも低くなりますので、底面積の変化のみで考えることができます。それに対して、上がった水面の高さがおもりの高さよりも高いか低いかわからない場合には、解き方が変わってきます。

　仮説を立てるという言い方は中学受験生の皆さんにとってわかりづらいと思われますが、「もしも上がった水面の高さがおもりの高さよりも高かった場合」として考える方法を使うことになります。
まず、水面の高さがおもりの高さを超える、つまりおもり全てが水の中に沈むとして、水面の高さを求めます。これはおもりの体積を容器の底面積で割ることで求められますが、この計算で求められる水面の高さがおもりの高さよりも低くなった場合、はじめの条件である「水面の高さがおもりの高さを超える」が間違っていることになります。

　よって水面の高さはおもりよりも低くなりますので、容器の底面積からおもりの底面積を引いた部分を底面積として、水の体積を割れば、水面を求めることができます。

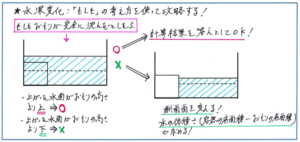
　水深変化の問題の全てで今回のような「もしも…」の考え方を使う必要はありませんので、問題文をよく読んで、容器とおもりの関係を正確に把握することが必要になります。また、場合分けをしなくとも、実際に計算をしてみて、おもりの高さを超えるはずであるのに計算結果が異なることに気づけば、そのまま条件を変えて解き進めることができます。

　ただ、解答方針をしっかり持っていなければ、「おもりの高さよりも高くなるはずなのに低くなった」と困惑してしまう事態に陥ってしまいます。確かな方針を持って問題に臨むことも組分けテストでは求められますので、そのためにも解法のひとつひとつの理解を深めておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。