メールマガジン宝箱 Mail magazine

　今回の5年生10月度グノレブ実力確認テストでは、旅人算をはじめ、流水算、時計算、通過算といった速さに関する単元がそろってテスト範囲となります。特に単元を問わず、「速さと比」という中学受験算数の最重要要素をどれだけ正確に使いこなせるかが高得点のポイントとなります。今回のグノレブ対策を通して、速さ・時間・距離の比の関係を的確に理解することが、今後の算数の得点力アップにつながります。

　また、「流水算」「時計算」「通過算」では、それぞれの単元に合わせで「図」を利用することが、応用問題での得点力を大きくアップさせます。

　「速さと比」の基本を徹底的に固めて、速さの応用問題を解くための図の活用方法を万全にしたうえでテストに臨みたいところです。そこで「速さと比」を中心に、10月度グノレブ実力確認テストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、グノレブ実力確認テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　旅人算：速さ・時間・距離の比の関係を正確に使いこなせていますか？】

　今回のグノレブは速さに関する問題が幅広くテスト範囲となりますが、どの単元においても基本としておさえておくべきが「比」を使った解法です。その中でも「旅人算」では、比の関係を使いこなせなければ解けない問題、比の関係を使いこなすことでより正確にスピーディーに解ける問題が多く出されます。

　速さにおける比の関係を使ううえでベースになるのは、「変わらない量（一定の量）」に着目することです。速さが一定であれば、距離の比と時間の比は等しくなり、時間が一定であれば、速さの比と距離の比が等しくなります。そして使う頻度がとても高くなるのが、距離が一定の場合の、速さの比と時間の比が逆比の関係になる点です。この逆比関係を正確に使いこなせれば、得点のチャンスが大きく広がりますので、理解が曖昧にならないように、徹底的に復習しておきましょう。

　速さと比を使うことで、通常の解法よりも計算が圧倒的に進めやすくなるケースもあります。例えば、「A君は分速75m、B君は分速45mで、200mはなれた地点から出発して同じ方向に進みます。A君は何m進んだところでB君に追いつきますか」といった問題では、比を使った解法の効果が発揮できます。

　比を使わない場合には、200÷(75－45)の式で、A君が追いつくまでの時間を求めて、その時間に75をかけることで距離が求められますが、ここで最初の式の結果が200/30と分数になることで、計算ミスが起こる可能性が上がってしまいます。

　そこで、同じ時間に進む距離の比が速さの比と一致することから、A君がB君に追いつくまでの時間に2人が進んだ距離の比が、75：45＝5：3となり、この比の差(5－3＝)2が200mにあたることから、200÷2×5＝500（m）と、距離を求めることができます。

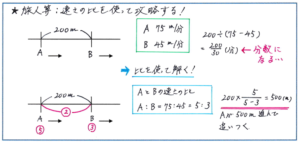
　速さと比に限ったことではありませんが、単元の理解が機械的になってしまうと、テストで解法を使いこなせなくなってしまいます。上のように、図にかき込みをするなどの方法で、比の関係を視覚的にもとらえるように進めて、理解を固めて行きましょう。

【第2位　旅人算：往復の旅人算で得点するために線分図を正しくかけていますか？】

　「旅人算」には、3人の旅人算や、時間よりも遅れたり早く着いたりするタイプの問題など、様々なパターンの問題が含まれます。その多くにおいて、図を的確に使うことが得点のポイントとなります。

　特に注意しておきたいのが、往復運動をする2人が出会うまでの様子を題材とした問題です。2人が動いた距離の和が、片道の何本分か、といった基本的な考え方をもとに、そこに比の考え方を加えるためには線分図での整理が必須となります。

　例えば、「太郎君がP地点を、次郎君がQ地点を同時に出発して、太郎君は、P→Q→Pと、次郎君はQ→P→Qと進みます。PQ間を3：1に分けるR地点で2人が2度目に出会ったとき、太郎君と次郎君の速さの比を求めなさい。」といった問題があるとします。

　複雑そうに見える問題ですが、線分図で問題内容を整理すると、一気に解答方針を立てることができるようになります。図は丁寧になり過ぎないように、アルファベットのＳのようなかたちで線をひくことができればそれで十分です。

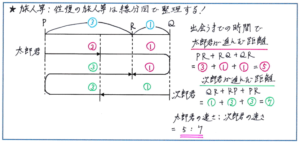
　ここで取り上げたような線分図を使って解くタイプの問題で比の関係を正確に使いこなせると、得点のチャンスが大きく広がります。図をかいて、そこに比の値をかき込むことで問題内容を整理することができますので、ためらわずに図をかけるように、練習を重ねておきましょう。

【第3位　流水算：流速が変化する問題について線分図を使いこなせていますか？】

　流水算では、静水時の速さ、流れの速さ（流速）、上りの速さ、下りの速さと、ひとつの問題で複数の速さが扱われますので、それぞれの関係を的確につかんでおくことが大前提となります。（上りの速さ）＝（静水時の速さ）－（流速）、（下りの速さ）＝（静水時の速さ）＋（流速）といった基本的内容については、できれば図を使わずに即時使えるようにしておきたいところです。

　同様に、2つの船が2つの地点から向かい合って進む場合に、旅人算の考え方で導き出すことができる、（船Aの下りの速さ）＋（船Bの上りの速さ）＝（船Aの静水時の速さ）＋（流速）＋（船Bの静水時の速さ）－（流速）＝（船Aの静水時の速さ）＋（船Bの静水時の速さ）と、2つの船の静水時の速さの和で解き進めることができる点も、必須内容としておさえておきましょう。

　注意すべきは静水時の速さや流速が上りと下りで変化するタイプの問題で、こうした問題を確実に得点できるようになれば、テスト全体の点数に安定感が生まれます。このうち静水時の速さが変化する問題については、変化する前後の状態を式にすることで、消去算の考え方を利用して解く方法が進めやすくなります。

　一方の流速が変化するタイプの問題では、下のような線分図を利用することで、変化の様子を的確につかんでスムーズに式を立てることができるようになります。

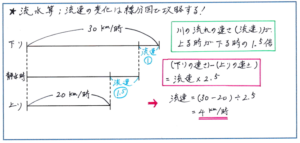
　もちろん、流速が変化するタイプの問題でも、消去算の考え方を利用して解くことができますが、図を使うことによって、計算する要素を最小限にとどめることができます。テスト全体からすると、流速が変化するタイプの問題はできる限り時間をかけずに得点しておきたいところです。図を使うと時間がかかりそうですが、計算の負担を大きく減らすことができますので、図をかく練習をしっかり重ねておくようにしましょう。

【第4位　時計算：計算を楽に進めるために、時計の図を活用できていますか？】

　時計算の基本としてまず注意しておきたいのが、「毎分5.5度」という数値を機械的に覚えて使うことがないようにすることです。1分間に6度進む時計の長針と、1分間に0.5度進む時計の短針の1分あたりの進む角度の差を表したのが「5.5度」ですので、問題によって、長針と短針の進む角度の和を使う必要がある際には当然使えなくなります。問題内容を正確にとらえて式を立てるように注意しましょう。

　そして問題を解く際には、時計の図を活用することが必須となります。例えば「3時と4時の間で時計の長針と短針が重なる時刻は3時何分ですか」といったタイプの問題であれば、旅人算の追いつきのパターンを使って、90÷(6－0.5)という式を、図をかくことなくしても立てられるでしょう。

　それに対して、例えば「4時と5時の間で、時計の長針と短針が反対方向をさして一直線になる時刻は4時何分ですか」といったタイプの問題では、頭の中で針の動きと角度の大きさをイメージするのは難しく、得点を逃してしまう結果になりかねません。そうした場合は必ず時計の図をかいて、針の動きをつかむようにしましょう。

　まずはスタートの4時ちょうどの図をかき、その時点で2つの針の間に120度の開きがあることをつかんだうえで、それから2つの針が重なるまでは角度は縮み続け、重なってから後に今度は角度が広がって行くため、そこから180度の開きになるまでの時間を求めればよいことがわかります。

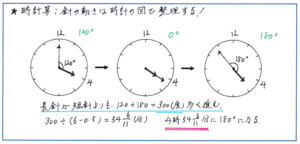
　時計算の応用問題になると、より2つの針の作る角度の大きさをイメージしづらくなります。時計の図を短時間で、ポイントをおさえるかたちでかけるように、普段から図をかく習慣を身につけておきましょう。

【第5位　通過算：長さの違いに着目して式を立てることができていますか？】

　通過算では、旅人算のような人が動くタイプの問題と異なり、動くものに「長さ」が加わる点が特徴となり、その長さを正確に扱うことが安定して正解を重ねるためのポイントとなります。そのためには、電車が移動する様子を図に表す解き方を習得する必要があります。

　単に電車Aが電車Bに追いついて追い越すパターンや、すれ違うパターンであれば、図を使わなくとも、電車Aと電車Bの長さの和を、速さの差（追い越すパターン）か、速さの和（すれ違うパターン）で割るという式がすぐに立てられますし、むしろ、図なしでも式をスピーディーに立てられるように練習を重ねておくことが必須となります。

　それに対して、例えば「ある電車が線路のそばに立っている人の前を通過するのに24秒かかります。また、この電車が480mのトンネルを通過するのに64秒かかります。この電車の長さは何mですか。」といった問題では、簡単にでも下のような図をかくことで、時間の差の(64－24＝)40秒が、トンネルの難が差480mを電車が進む時間にあたることが、すぐに把握できます。

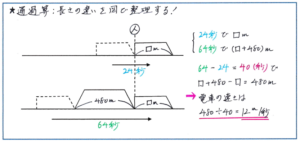
　この他にも、異なる速さ、長さの2つの電車が、同じトンネルを通過する時間がそれぞれ与えられているような問題でも、それぞれが通過する様子を図にすることで、どの部分の違いに着目すればよいのかを瞬時につかむことができます。

　流水算、時計算と同様に、図をかいて解くことのメリットは大きいですが、一方で図をかく時間に多くの時間をかけ過ぎてしまうことは、テスト全体を進めるうえで時間配分を難しくしてしまいます。図はポイントがかき込めればよいので、例えば電車の図などは、シンプルに、丁寧になり過ぎないように注意しながら、図をかく練習を重ねておくようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。