メールマガジン宝箱 Mail magazine

　今回の5年生第6回組分けテストでは、夏期講習で基本的な内容を演習した「比」について、それを応用させた倍数算、平面図形といった様々な問題を通して、レベルアップした比の活用方法の理解度を確かめる問題が多く出されます。

　次回（11月）の第7回組分けでは、速さと比など、さらに難度の高い問題が待ち受けていますので、基本から発展への重要な「つなぎ」となる今回の内容を確実に理解できているかどうか、しっかりチェックしておきたいところです。さらにつるかめ算の応用と年令算という入試頻出の重要単元も含まれる大事なテストです。

　そこで「比」に関する単元を中心に、第6回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形と比：三角形の共通する角度を見つけ出す視点を身につけられていますか？】

　今回の組分けテストの中でも特に注意すべき単元は『予習シリーズ5年下』の第2回・第3回で演習した「平面図形と比」です。平面図形の問題を比を使って解き進めて行くのですが、この単元は実際の入試でも出題頻度が非常に高く、得点差が大きくつく問題になるケースがとても多いです。

　特に、三角形を題材とした問題では、相似、面積比どちらの場合でも「共通する角を持つ三角形」を正確に見つけ出すことがポイントになります。相似における三角形の問題で特に注意しておきたいのは、三角形や長方形を折り曲げるタイプの問題です。ここでは、基本的なクロス型やピラミッド型の図形とは異なる見方が必要になります。

　対策として、折り曲げによって生まれる三角形の角度のうち、どの角度が共通しているかについて、実際に図形の中にマークや記号を書きこむことで、視覚的にとらえるようにすることが有効となります。図を見たままに頭の中で角度の関係をつかもうとすると、思わぬミスが起きてしまいます。三角形の向きが変わるだけで見間違いが多くなりますので、書きこみをして共通する角度を見つけ出し、解答の材料にしましょう。

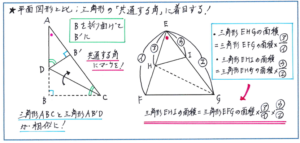
　面積比の問題では、「共通の角を持つ三角形の面積の関係」について、予習シリーズでも33ページの枠内で示された分数式の積のかたちで表す方法をしっかりとおさえておきましょう。この式については、長さを取り違えないように気をつけて暗記しておけば正解となるチャンスが大きく広がりますが、忘れてしまった場合でも、上の右の図のように式の成り立ちを振り返えればよいでしょう。

　相似の問題では図形の「向き」にも気をつけておきたいところです。向きの変化に惑わされて長さを取り違えてしまうと、基本的な難度の問題でも得点を逃してしまいます。ミスを起こさないように、マークや記号を図に書き入れて解く方法を練習しておきましょう。

【第2位　平面図形と比：平行四辺形の内部にある長さの比を正確に求められていますか？】

　平面図形と比の問題では、長方形を含む平行四辺形を題材とする問題の頻出度が、三角形をしのぐほどに高く、組分けテストでも出題される可能性が高くあります。向い合う2組の辺が平行という平行四辺形の性質から、相似の関係にある図形が生まれやすく、また「高さが共通」のケースが多くあることで、「面積比＝底辺の長さの比」もまた多く使われるというのがその理由です。

　特に平行四辺形の問題で注意しておきたいのが、「1つの長さを2つの異なる比で分ける」タイプの問題です。バラバラの比について、それぞれの比の値を足した数字を最小公倍数にそろえて、比の数を変化させるという方法で解き進めますが、この解法は今後、速さの問題でも使われることがありますので、今回の演習で解法を確実に理解しておきましょう。

　基本となるのはクロス型の相似の関係ですので、まずは平行四辺形（長方形）の中にあるクロス型の相似の関係を見つけ出すことに集中しましょう。平行四辺形や長方形の問題が出されたら、まずクロス型を見つける、というスタンスを徹底するとよいでしょう。相似の関係が見つかったら、下の図のように相似比を図の中に書きこみます。この書きこみをしておけば、長さを取り違えることなく、最小公倍数を求める段階に進むことができます。

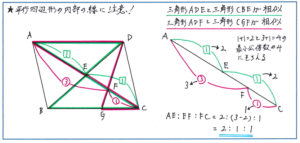
　最小公倍数を用いて比の数をそろえた後は、図をよく見て求める比の長さを選んで行けばスムーズに正解に行き着くことができます。

　一見すると複雑に感じられる問題ですが、ひとつひとつの手順を正確に行えば、大きな負担なく正解へと行き着くことができます。主にテストの中盤から後半の大問の中で出されることが多い問題であるため、得点できれば差がつけられますので、解法を確実に固めておきましょう。

【第3位　比の利用：解き方を丸覚えする前に、式で理解を固めましょう！】

　5年の後期からは夏期講習で習った「比の基本」を踏まえて、様々なタイプの文章題に取り組んで行きますが、すべての問題において、比の基本の理解が大前提となりますので、少しでも理解が曖昧な部分が見つかった場合には、すぐに夏期テキストに戻って復習しましょう。

　特に逆比、連比の考え方・求め方は、今後の速さや図形の問題で数え切れないほど使うことになりますので、確実な理解が必要です。基本的な解法を丸覚えするのではなく、式のかたちで理解を固めることに注意しましょう。

　例えばA：B＝4：3の場合の逆比の求め方で、4と3を入れ替えれば3：4とすぐに答えを求められるのですが、そうした機械的な覚え方に頼ってしまうと、今後、今後、A：B：C＝4：3：2と3つの比についての逆比を求める際に、どのように解けばよいのかわからなくなってしまいます。

　4：3の逆比を求める際には、4と3を分母に、分子を1とした「分数の比」が逆比の姿であることをしっかり踏まえておきましょう。その解き方を固められていれば、A：B：C＝4：3：2の逆比であっても、1/4：1/3：1/2＝3：4：6と求められます。「逆比だから入れ替える」という考え方ではなく、分数の比を利用することを徹底しましょう。

　また、「比の積・比の商」で扱う「金額の比」では、基本となる「枚数＝（合計代金）÷（1枚の代金）」の式に立ち返るように注意しましょう。例えば、「10円玉と50円玉が何枚かあり、10円玉だけの合計金額と50円玉だけの合計金額の比が2：3のとき、10円玉と50円玉の枚数の比を求めなさい。」という問題でも、基本の式に立ち返れば、10：50＝1：5より、2/1：3/5＝10：3と正解に至ることができます。

　中学受験算数の最重要単元である比だからこそ、ただ解き方を機械的に丸覚えするのではなく、基本となる式の理解をしっかり固めるようにしてください。それがこれからの算数の演習の理解度を大幅にアップさせる重要な足がかりになります。

【第4位　つるかめ算の応用：様々なタイプのつるかめ算の解き方を使い分けられていますか？】

　『予習シリーズ5年下』の第4回で演習する「つるかめ算の応用型」には、様々なタイプの問題が含まれます。この単元については、それぞれの解き方を確実に理解していないと、式を立てることもできず、大問の(1)でさえ得点ができなくなってしまいます。逆に解法さえ確実に理解できていれば、パターンに合わせた解き方で正解を得ることができる単元でもあります。まずは『予習シリーズ』の解説をじっくりと読み込んで、基本的理解を徹底的に固めてください。

　今回の組分けテスト対策で特に注意しておきたいのが、条件不足のつるかめ算の中にある「いもづる算」です。通常のつるかめ算では1つあたりの量と個数の合計、そして全体の量が与えられるのですが、この中の個数の合計がわかっていない場合の解き方がいもづる算（不定方程式とも言います）です。

　一見するとあてはまる数の組合せが無限にあるように感じられて、どこから手をつければよいのかわからなくなってしまいますが、まずは問題の内容を正確に式にすることに集中しましょう。そして、その式を約分の考え方で簡単にした後からがポイントになります。ここで手間を惜しむことなく表をかいて、あてはまる数の組合せを選び出して行きましょう。

　表をかくと聞くと面倒に感じてしまうお子様が多いですが、いもづる算でかく表はいたってシンプルですし、枠の線なども丁寧にかく必要はありません。フリーハンドで枠をかいて、あとは数を書きこむだけです。いもづる算で大事なことは、数の増減の規則を確実につかむこと。「aが4減る代わりに、bが7増える」といった増減の規則が、表を使うことでよりはっきりと把握できるのです。この表を残しておくことで、見直しが進めやすいという大きなメリットもあります。

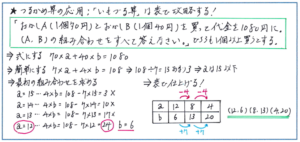
　今回の組分けテストのメインとなるのは、やはり「比」に関連する単元ですが、このつるかめ算の応用型も問題のタイプによって解法を柔軟に当てはめる力が試される点で、決して軽視できない重要単元です。比の対策に注力し過ぎて、このつるかめ算の応用型、そしてこの後に解説する年令算の対策がおろそかにならないように、十分に注意してください。

【第5位　年令算：3人以上の年令の変化に正確に対応できていますか？】

　年令算では、年数が経つことで、問題に出てくる誰もが同じだけ年をとることから、「年令の差は常に一定である」ことが大前提となります。この点を踏まえれば、基本的な問題は線分図を利用することでスムーズに正解に行き着くことができます。

　注意すべきは「3人以上」の年令の関係が問題の対象となった場合です。例えば「現在、父が40才、母が34才で、2人の子どもが9才、5才のとき、父と母の年令の和が、2人の子どもの年令の和の3倍になるのは、今から何年後ですか」といった問題。ここで父と母の2人に対して、子どもの人数が3人や4人と、2人とは異なる場合には、マル1年後の年令の和を式に表して、分配法則を利用するという解法を使うことになりますが、この問題のように、子どもの人数が、父と母と同じ2人である場合には、より簡単に解き進めることができます。

　父と母の年令の和が1年後に、1＋1＝2（才）増えるのに対して、2人の子どもの年令の和も、1＋1＝2（才）増えるので、何年経っても、父と母の年令の和と2人の子どもの年令の和は変わらない、つまり「年令の差は常に一定」という年令算の大原則にそって解き進めることができるのです。

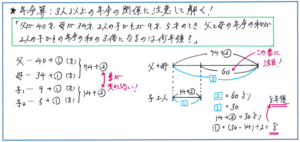
　扱う人数が増えたからといって、マル1年後という式のかたちで解く、と決めつけるのではなく、大人2人に対して子供も2人なのだから、年令差は変わらない、と柔軟に対応する必要があります。そうした点に気づけるかどうかも、どれだけ「年令の差」に着目できているかによります。

　解答を求める際に、最後に2で割って年数を求めることにも十分に注意しておきましょう。計算で答えが求められた後に、実際にその年数をあてはめて、父と母の年令の和が2人の年令の和の3倍になっているのか、すぐに確かめるとよいでしょう。年令算は検算（見直し）がやりやすい特徴がありますので、式をしっかり残しておけば、短時間で見直すことができます。ぜひ見直しの方法まで練習しておくようにしてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。