メールマガジン宝箱 Mail magazine

　今回の5年生11月度グノレブ実力確認テストでは、仕事算、倍数算、相当算・還元算、ニュートン算といった、「比と割合の文章題」の単元がそろってテスト範囲となります。数量を比で表して式を立てる、線分図を活用して問題内容を整理するといった比と割合を使った解法をどれだけスピーディーに、正確に駆使できるかが高得点のポイントとなります。今回のグノレブ対策を通して、比と割合を使った解法を定着させることは、単元を問わず今後の算数の得点力アップにつながります。

　数量を比で表す方法、線分図の正確なかき方をしっかり覚え込んだうえでテストに臨みたいところです。そこで、重要単元「比と割合の文章題」がテスト範囲となる11月度グノレブ実力確認テストの対策ポイントを、第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、グノレブ実力確認テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　倍数算：和一定でも差一定でもない「倍数変化算」の解法を定着できていますか？】

　「倍数算」の中で、例えば「姉は1200円、妹は800円持っていて、2人とも同じ金額を使ったところ、姉の所持金と妹の所持金の比が3：1になりました」といった差が一定の問題や、「兄と弟の所持金の比が4：1だったところ、兄から弟に200円を渡すと2人の所持金の比が3：2になりました」といった和が一定の問題であれば、線分図をかく、あるいは比をマルで表して、比例式で解くといった解法パターンを使って式を立てることがスムーズにできます。

　こうした「同じ量」に着目して解く問題は、今回のグノレブの中で必答問題になりますので、ここでの理解が曖昧な場合はすぐにテキストの復習を進めてください。

　得点の分かれ目になるのは、「同じ量」が見つからない、「倍数変化算」を確実に得点できるかどうかです。例えば、「AさんとBさんの所持金の比は3：2でした。Aさんは400円をもらい、Bさんは800円使ったので、Aさんの所持金とBさんの所持金の比が5：2になりました」といった問題。

　ここで、はじめのAさんの所持金をマル3、Bさんの所持金をマル2とすることまでは必須としたうえで、ここからは2つの解法を使うことができます。

　一つ目は、現在のAさんの所持金をシカク5、Bさんの所持金をシカク2として、下のように、Aさん、Bさんの所持金の変化を式にするパターンです。シカクの5と2を最小公倍数の10にそろえて、消去算の考え方で解く方法です。

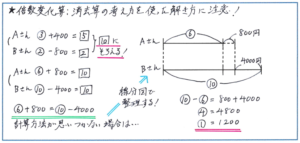
　二つ目は、(マル3＋400)：(マル2－800)＝5：2といった比例式を立てて、ここから「比の内積＝比の外積」の性質を使い、2×(マル3＋400)＝5×(マル2－800)の式から、マル6＋800＝マル10－4000の式にして解くパターンです。

　どちらの解法においても共通して注意したいのが、数の加減でミスをしないようにすることです。グノーブルでは数学でいう「移項」の考え方を早期から学習しており、数のプラスマイナスの扱いには慣れていると思われますので、マル6＋800＝マル10－4000から、マル4＝4800にスムーズに移行できるでしょうが、迷ってしまいそうな場合は、上記のような線分図を簡単にかいて解くことをおすすめします。

　「倍数変化算」で確実に得点するために、問題内容を正確に式にすることに徹底的に注意しましょう。

【第2位　相当算・還元算：やりとりの問題で、数の変化を図で整理する解法が使えていますか？】

　「相当算・還元算」の中には、問題文が長く複雑に見える問題が多く含まれます。今回のグノレブはテスト全体の問題数が多くなることが予想され、制限時間内に少しでも多くの問題を解くためには、そうした問題文にボリュームがある問題をスピーディーに解き進める必要があります。

　問題文を整理するためには図が必須になりますが、図をかくのに時間をかけ過ぎることは何とか避けたいところです。そのためにも普段の演習から図をかく練習を重ねて、それぞれのパターンでどこに注意して図をかけばよいかをおさえておくようにしましょう。

　まずは、「やりとり」の問題です。例えば「春子さん、夏子さん、秋子さんの3人がリンゴを合わせて81個持っていました。まず、春子さんが持っていたリンゴの1/3を夏子さんに渡し、次に夏子さんがそのとき持っていたリンゴの2/5を秋子さんに渡し、次に秋子さんがそのとき持っていたリンゴの1/4を春子さんに渡したところ、3人の持っているリンゴの個数が等しくなりました。はじめに春子さんは何個のリンゴを持っていましたか」といった問題を考えてみましょう。

　ここから3人のやりとりの様子を図にして考えるのですが、ポイントとなるのは2点。まず、3人の持ているリンゴの合計個数が81個であることが変わらないこと、そして図を完成させるにあたっては、実際のやりとりの順番通りではなく、最後の状態から「さかのぼって」うめる必要があることです。

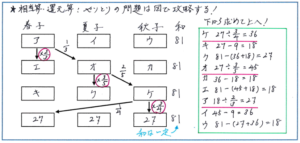
　数値を埋めるにあたっては、リンゴを渡す前の個数に着目しましょう。例えば、冬子さんが春子さんに持っていたリンゴの1/4を渡したということは、残ったリンゴの個数が渡す前の3/4になった、といった考え方です。

　また、図をかく際には、上記のような枠までかかなくても構いませんので、数字の変化が正確にわかるように、間隔をあけて数字を埋めて行くようにしましょう。

【第3位　相当算・還元算：もとにする量が変化する問題を線分図で整理できていますか？】

　相当算・還元算の中で、【第2位】で取り上げた「やりとり」と同じく、お金を段階を分けて使うようなタイプの問題もまた、問題文の分量が多くなることがあります。例えば、「冬子さんは持っていた金額の1/4より150円少ない金額でケーキを買い、残りの金額の2/3で本を買いました。その後、父から300円をもらったので、そのときの金額の2/5よりも60円多い金額で果物を買うと420円が残りました。冬子さんがはじめに持っていた金額は何円ですか」といった問題は、どのように考えればよいでしょうか。

　こうした問題も図を使って整理する点は「やりとり」と同じですが、図のタイプが全く異なり、線分図が有効となる点に注意しましょう。使った金額は分数で表されますが、この問題のように「もとにする量」が次々に変化する場合は、整数を使うと計算が圧倒的に進めやすくなります。

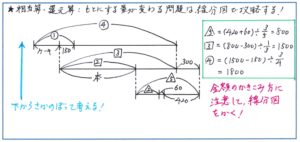
　この問題でも「やりとり」のように、実際にお金を使った順番とは逆に、残った金額からさかのぼって数値の変化をとらえて行きます。問題によって、解答の出発点がどこになるのかに気をつけて解き進めることを、強く意識しましょう。

【第4位　仕事算：「休み」が出るパターンの式の意味を正しく理解できていますか？】

　仕事算の中で、複数の人数で仕事に取り組む際に、どちらかがある日数を休んでしまう場合がありますが、このタイプの問題の式の意味を正しく理解できているでしょうか。

　例えば「ある仕事をするのに、Aさん1人では24日かかり、AさんとBさんの2人では15日かかります。この仕事をAさんとBさんの2人ですることにしましたが、途中でAさんが8日休みました。仕事を終えるまでに全部で何日かかりましたか」といった問題について考えてみます。

　仕事の全体量を24と15の最小公倍数の120とすると、Aさんの1日の仕事量が、(120÷24＝)5、2人合わせての1日の仕事量が、(120÷15＝)8になる、という段階まではスムーズに進められるでしょう。もちろん全体の仕事量を1として、Aさん、2人合わせての1日の仕事量をそれぞれ、1/24、1/15としても構いません。ここでは分数計算を極力少なくするために、最小公倍数で進めています。

　ここから、Aさんが8日休んだので、その分の仕事量、(5×8＝)40を全体の仕事量120に足して、(120＋40＝)160としたうえで、それを2人合わせての1日の仕事量である8で割って、160÷8＝20（日）として求められますが、この「休んだ仕事量を足す」という考え方がなぜ成り立つのかまで正しく理解せずに、ただ解法を丸暗記してしまうと、問題の出され方が少しでも変わった際に、対応できなくなってしまうことがあります。

　そこで下の図のように問題内容を整理すると、休んだ分の仕事量を足すことの意味をつかめるようになります。

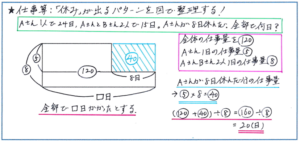
　上記の図のようなかたちで一度問題内容を整理しておけば、問題の設定が複雑になった場合でも正しく対応できるようになります。この問題に限らず、解法をパターンで覚えることに終始せず、なぜそのような式になるのか、と意識する習慣を5年生のうちに身につけておくことが、6年生になってからの得点力のアップにつながります。

【第5位　ニュートン算：長さの違いに着目して式を立てることができていますか？】

　ニュートン算は独特な問題設定のため、難度が高いという印象を持たれがちですが、解法を確実に理解できれば、出題パターンは限られますので、テストで得点源にすることができる単元です。

　そのための大前提となるのが、線分図を使って問題内容を整理することにあります。問題の中には、線分図を使わなくとも式が立てられるタイプの問題もあり、それらはテキストの前半に収録されていますので、解説をよく読んで、式の立て方をマスターしておくようにしましょう。

　ここでは、線分図を使って解く典型的な問題を題材とします。線分図をかく際のポイントは、わからない数値について記号を使って表すことにあります。例えば次のような問題です。

　「ある牧場では、はじめにある量の草が生えていて、さらに毎日一定も割合で草が生えてきます。この牧場で、もし羊26頭を放し飼いにすると40日で生えている草がなくなります。また、もし羊46頭を放し飼いにすると20日で生えている草がなくなります。どの羊も1日に食べる草の量は同じであるものとします。この牧場に羊31頭を放し飼いにすると草は何日でなくなりますか」

　ニュートン算の解きづらいところは、増える量と減る量が同時進行で進むところにあり、そうした状況を図にするにあたって、例えば相当算や年令算などの問題とは違った難しさが感じられてしまうかもしれません。

　気をつけるのは、分からない数を記号にすることで、ここではまず、はじめに生えている草の量をサンカクとします。そしてポイントは、羊1頭が1日に食べる草の量をマル1とすることです。羊は、はじめに生えている草と、後から生えてくる草を「合わせて」食べることになります。このようなまとめて処理をする量をマルとすると、図がかきやすくなります。ポンプで井戸の水をくみ出す場合であれば、ポンプ1台が決まった時間にくみ出す量をマル1とすることになります。

　あとは、羊26頭の場合と羊46頭の場合にわけて線分図にして、後から生えた草の量を、それぞれはじめに生えている草の量につなげれば、図は完成です。

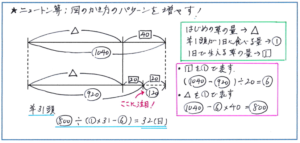
　解法の手順は、1日で生える草の量をマルで表す→はじめに生えている草の量もマルで表す→羊31頭の場合をマルで計算する、といった流れになります。この流れもしっかり頭の中に定着させておくようにしましょう。線分図のかき方、そこからの解法の流れをマスターできれば、複雑に見えるニュートン算も攻略することができます。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。