メールマガジン宝箱 Mail magazine

　今回の5年生12月度グノレブ実力確認テストでは、面積比、相似形、かげ・折り返し、図形の移動といった、図形と比の単元が目白押しです。まさに入試頻出の図形問題のオンパレードとなります。

　与えられた図形の中から相似の関係、面積比と共通の長さの比をいかに正確に見つけ出すか、同じ長さ、角度の関係を解法に利用できるかが高得点のポイントとなります。今回のグノレブ対策を通して、図形問題での比を使った解法を定着させることは、入試問題で出題される図形問題を攻略するための重重要な基礎固めにつながります。

　面積比、相似形の基本的な解法の理解をがっちりと固めたうえでテストに臨みたいところです。そこで、重要単元「図形と比」がテスト範囲となる12月度グノレブ実力確認テストの対策ポイントを、第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの算数予想問題と組み合わせれば、グノレブ実力確認テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　相似形：相似の関係を利用するための補助線の引き方は理解できていますか？】

　「相似形」では、まずは砂時計型やピラミッド型の典型的な形での長さの比の関係を間違えないように注意することが大前提となります。テキストのはじめに出てくるような典型的な形で比の取り方に間違えがある場合には、徹底的に反復練習をして、解き方を固めてください。

　そのうえで注意すべきは、与えられた図の中に相似の関係がない場合に、自分で補助線を引いて相似の関係を作り出すパターンです。ここで何よりも優先して着目するのは「平行線」です。相似の基本は平行線にありますので、自分で相似の関係を作る場合にも、平行線を見逃さないように気をつけてください。

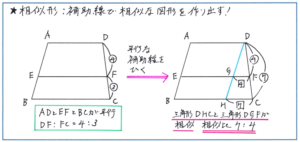
　例えば下の左の図の場合、ADとEFとBCが平行になりますが、台形ABCDと台形ADEF、台形EFBCはどれも相似の関係にはありません。そこで相似の関係にある三角形を作るために、Dを通ってABに平行な直線を引いて、BCとの交点をH、EFとの交点をGとすると、三角形DHCと三角形DGFというピラミッド型の相似を作り出すことができます。

　ここで気をつけて頂きたいのが、GF：HCと等しいのはDF：DCであってええ、DF：FCではないということです。これは先に触れた相似の基本でも注意すべきポイントですが、補助線を引くという作業をひとつ加えることで、つい比の基本の関係を間違えてしまうというケースが、実際のテストの緊張感の中で起こりがちです。基本的な部分での取りこぼしがないように慎重に取り組みましょう。

　ここでご紹介した内容は、補助線を引くパターンの解法の中でも基本的なものになります。問題の難度が上がると、より複雑な図形の中に補助線を引くことが求められ、図形の外側に線を延長させる「角（つの）出し」といった解法が必要になることがあります。まずは、上記のような基本的な補助線の引き方を確実に理解して、平行線に着目する意識をしっかり高めておきましょう。

【第2位　相似形：1つの直線を2種の比で分ける解法は確実に使いこなせていますか？】

　相似形の問題の中で、図形の中にある直線を「AD：DE：EF」のような3項の比に分けるかたちの比を求めさせるタイプの出題があります。問題としてはテスト中盤から後半の、例えば小問3題構成の大問の(2)で出されるケースが多く、まさに得点の分かれ目となることが多いです。

　こうした問題を解くうえで必要となるのが、「比をそろえる」という考え方です。具体的な図でその内容を考えてみましょう。下の図では平行四辺形ABCDに対して、対角線の交点をE、BG：GC＝1：2として、BF：FE：EDを求めるといった場合、どのように解き進めればよいでしょうか。

　対角線BDに注目して、BDを含む三角形の相似の関係を見つけ出して行きます。基本となるのはクロス型の相似の関係ですので、まずは平行四辺形の中にあるクロス型の相似の関係を見つけ出すことに集中してみると、三角形ADEと三角形CBE、三角形ADFと三角形GBFという2つの相似の関係を見つけることができます。この問題に限らず、平行四辺形や長方形の問題が出されたら、まずクロス型を見つける、というスタンスを徹底するとよいでしょう。

　相似の関係が見つかったら、下の図のように相似比を図の中に書きこみます。この書きこみをしておけば、長さを取り違えることなく、最小公倍数を求める段階に進むことができます。

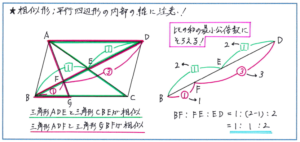
　そしてポイントとなるのが、1：1と1：3という2つの比の和（1＋1＝2と1＋3＝4）を、最小公倍数の4にそろえるという解法です。この比をそろえる解法は、この後の【第3位】にも出てきますし、速さの問題でも使う重要な方法です。

　一見すると複雑に感じられる問題ですが、ひとつひとつの手順を正確に行って解法を着実に身につければ、大きな負担なく正解へと行き着くことができ、得点できれば差がつけられますので、解法を確実に固めておきましょう。

【第3位　面積比：長さの比を「そろえて」面積比を求める解法を覚え込めていますか？】

　面積比の問題では、「高さが同じ図形の面積比は底辺の長さの比と等しい」という考え方が基本になります。

　典型的な基本問題では、ひとつの三角形の頂点から向かい合う辺に引いた線で分けられる三角形の面積比を、底辺の比から求めるといったタイプの出題になります。また、同じ高さの三角形と台形の面積比を求める際には、三角形の底辺の長さと、台形の「上底の長さと下底の長さの和」の比で考えることに注意が必要です。

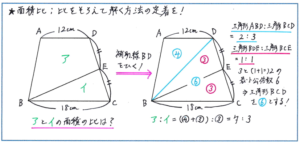
　それを応用した下の図のような問題で、解答方針をスムーズに立てられているでしょうか。

　四角形ABCDはADとBCが平行な台形であることから、BとDを結ぶ線を引くと、三角形ADBと三角形BCDは高さが共通のため、面積比は、12：18＝2：3となります。

　次に三角形BCDに着目すると、CDを底辺とするとDE：CE＝1：1より、三角形BDEの面積と三角形BCEの面積の比は1：1となります。

　ここで三角形BCDの面積を、3と1＋1＝2の最小公倍数6から⑥とすると、三角形ADBの面積は、⑥×2/3＝④、三角形BDEの面積は⑥×1/2＝③となります。このように、【第2位】と同じように最小公倍数を利用して比をそろえることが、このタイプの問題を解くうえでのポイントとなります。

　以上より、四角形ABEDの面積は④＋③＝⑦、三角形BCEの面積は③となることから、アの面積とイの面積の比を、7：3と求めることができます。

　このタイプの問題は、補助線を引く、最小公倍数を利用して比をそろえるといった重要な考え方を組み合わせて解く力が求められるため、要注意の問題です。スムーズに解き進められるように、解答のポイントをしっかりおさえておきましょう。

【第4位　折り返し：同じ長さ、同じ角度の移動を正確に追いかけられていますか？】

　「折り返し」の問題では、折り返しによって生まれる相似の関係を的確につかむことが、正解を得るために必須となりますが、そこで生まれる相似の関係が、ピラミッド型や砂時計型といった基本的なパターンではないために、ちょっとした見逃がしで、相似の関係を見逃してしまうことがあります。

　そうした事態を防ぐためにポイントとなるのが、「同じ長さ、同じ角度の移動」を正確に追うことです。特に角度について、90度をはさむ角度の大きさに注目できるかどうかが、得点の分かれ目になります。

　例えば下の図のように、正方形を折り返した場合、どの図形が相似の関係にあるか、瞬時に把握することができるでしょうか。

　まずは元の図形が正方形であることから、90度を含む三角形に着目します。そしてポイントとなるのが、三角形BMHと三角形CFMで、角BMHを○、角CMFを×とすると、角HMFが90度であることから、○＋×は、180－90＝90（度）となります。ここで、三角形BMHにおいて角HBMが90度であるため、角BMHと角BHMの和が90度になり、角BHMが×となります。

　同じ流れで、三角形CFMにおいて角CFMが○になるため、三角形BMHと三角形CFMは相似になります。

　また、三角形BMHと三角形GEHにおいて、角MBH＝角EDH＝90度、角BHM＝角GHE＝×（対頂角）より、三角形BMHと三角形GEHが相似になり、角GEHは○と表すことができます。

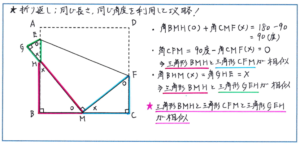
　これにより、三角形BMHと三角形CFM、三角形GEHという3つの三角形が相似の関係にあることがわかりましたが、注意すべきは、この相似の関係を使って長さを求めさせるケースがほとんどですので、相似の三角形の中で、互いに対応する辺をおさえておく必要がある点です。そのため、○、×の記号はそのまま残して、○→×の方向が同じ辺が対応する（MHとFMとEH）と視覚的に把握できるようにしておけば、その後の作業が断然楽になります。

　複雑な図形が出来上がる「折り返し」ですが、同じ角度を記号で統一して図形に記号をかき込む作業を定着させておけば、一気に難度のハードルが下がります。

【第5位　図形の移動：重なりの面積が2回あるときの解き進め方に要注意です！】

　図形の移動の問題には、円や三角形が多角形の内部や外部を転がって移動するタイプの問題や、おうぎ形や三角形が直線上を回転しながら移動するタイプの問題がありますが、どのタイプも共通して、自分で図をかいて移動の様子を的確に把握する解法が必要となります。普段の演習から、特に回転移動の場合は「角度」に注意して、自分で図をかいて遠く練習を積み重ねておきましょう。

　回転移動ではなく、直施上を図形が平行移動して、図形の重なり部分の面積を求めるタイプの問題では、あてはまる面積が2回あるパターンの解き方に注意が必要となります。

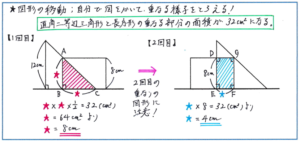
　例えば下の図のように、直角二等辺三角形が長方形に向かって直線上を移動して、2つの図形が重なる部分の面積が32平方cmになる場合を求める際に、1回目の重なりの図形は、もとの直角二等辺三角形と相似の関係にある直角二等辺三角形となるため、三角形の面積の公式で長さを求めることができます。

　ポイントになるのは2回目に重なりの部分の面積が32平方cmになる場合で、ここでは回転移動と同じように、自分で図をかいて、重なりの部分がどのような図形になるかを確かめる必要があります。図をかく場合には、丁寧にかき過ぎると時間がかかってしまいますが、少なくとも長さの関係が正確にとらえられるようなかき方をするように注意しましょう。

　また、平行移動の場合、移動した長さを正確に求めるためには、図形そのものの移動で考えるよりも、移動する図形の1つの頂点に印をつけて、その頂点が移動した長さでとらえる方がミスを防ぐことができます。細かなミスがないように注意深く進めましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。