メールマガジン宝箱 Mail magazine

　今回の6年生5月度グノレブ実力確認テストは、「2量の関係」「小数・分数」「立体図形」といった、パターン化された解法を正確に使いこなす力が求められる重要単元がテスト範囲となります。

　立体図形の切断での切断面のつくり方、時刻のずれでの比の使い方、単位分数の和を題材とした問題での式の立て方といった解き方のルールをしっかり覚えて臨むことで、複雑に見える難問でも、スムーズに正解まで行き着くことができます。

　問題内容に応じた解き方のパターンをしっかり覚え込み、解答方針を立てる力が試される5月度 グノレブ実力確認テストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、グノレブ実力確認テスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　立体図形：おもりを沈める問題では水面の高さに要注意です！】

　立体図形の水深が変化する問題の中で、おもりを沈めるタイプの問題では、「水面の高さとおもりの高さの関係」に十分に注意する必要があります。

　おもりを沈めるタイプの問題で共通して大前提となるのが、「沈めた部分の体積と、上がった水面の分の体積が等しい」ことです。まずはこの大前提にしたがって、体積を求める計算を正確に進められるように、基本問題で確認しておきましょう。

　そのうえで気をつけるべきは、おもりを沈めた際の水面の高さが、「おもりの高さの上に来るのか、下に留まるかの違い」です。この違いによって解き方が大きく変わってきますので、確認を曖昧にしておかないようにしてください。

　例えばおもりを沈める前から水面の高さがおもりの高さよりも上にある場合には、おもりの体積を水そうの底面積で割る、といった解き方に迷わず進むことができます。ただ、そのような高さの違いが明らかな場合ではなく、「おもりを沈めた際に水面の高さがおもりの高さを超えるかどうかがわからない場合」に注意が必要になるのです。

　そのような場合は、「仮に」の解き方で進めます。下の通り、まずは「おもりが完全に水の中に沈む」という前提のもとで計算を進めます。その結果出た水面の高さがおもりの高さを超えた場合はそのまま進めることができます。

　一方、計算で出した水面の高さがおもりの高さより低かった場合は、前提が間違っていたとなりますので、水面はおもりの高さよりも低いことになります。その場合は、水の体積を、「水そうの底面積からおもりの底面積を引いた面積」で割れば、スムーズに正解に行き着きます。

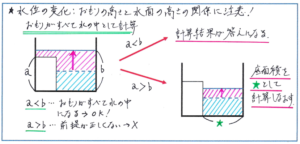
　中学から習う数学では、この「仮に」の解法は多く使うことがありますが、中学受験生のお子様方にとっては、なかなか理解しづらい解法になります。この水位の高さの問題は、「仮に」の解き方の基本を身につける絶好の機会となりますので、ぜひじっくりと理解を固めてください。

【第2位　立体図形：切断の基本ルールを正確に覚え込まれていますか？】

　今回のグノレブにおける立体図形の重要単元のひとつが「立体の切断」です。立方体や直方体、さらには三角すいといった立体を切断する平面によってできる面積や体積、長さを求めるといった問題で、かつて中学入試では男子難関校で多く出題されていましたが、現在では男子校・女子校を問わず中堅校まで幅広く出題対象とされています。それだけに今回のグノレブ対策を通じて、しっかり理解を固めて問題対応力を高めておきたいところです。

　まずはテキスト【立体図形(2)】の最初のページで問題となっている10個のパターンを徹底的に頭の中にたたき込んでおきましょう。できれば何も書かない状態のテキストのコピーをとって、何度でも練習できるようにしておくと理解をガッチリと固められます。

　この5個の中で特に気をつけておきたいのが、(6)の等脚台形になるパターンで、このパターンはテストでの頻出度がとても高いです。「向かい合う面に引かれた切断線が平行になる」という大前提のもと、台形の上底・下底にあたる線を速く正確に引くことができるようになるまで練習を重ねましょう。

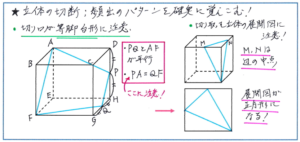
　また、上の右の図のような、立方体を1頂点と2つの中点で切断（テキストの(2)のタイプ）してできる三角すいの展開図が正方形になるというパターンもテスト頻出ですので、しっかりおさえておきましょう。

【第3位　2量の関係：パターン化された解法を的確に使いこなせていますか？】

　今回のテスト範囲の「2量の関係」では、問題ごとのパターン化された解法を覚え込み、的確に使いこなす力が試されます。

　特に、タクシー料金に代表される、2つの量の変化が特徴的な問題、そして一定の割合で遅れたり、進んだりする時計を扱う「時刻のずれ」の問題では、解き方が固まっていないと時間ばかりがかかって結果、正解に至れないケースが多くなってしまいますが、パターン化された解法を確実に使いこなせれば、得点源にできる可能性が大きく広がります。

　タクシー料金型の問題については、「加算された回数」の把握がポイントとなります。グノーブルのテキストでは、この「加算回数」について、グラフでは解説されていませんが、式の成り立ちの理解を促し、イメージを固めるうえでは、グラフもひとつの有効ツールとなりますので、ここではグラフをご紹介します。すでに「加算回数」について理解を固められている場合であれば参考で構いませんので、解法を確認してみてください。

　くり返しになりますが、ポイントは「加算回数」を間違わないことにあります。そして、計算で求められた加算回数を正確に用いて、幅のある値のどこが求められているのかを間違わないように注意しましょう。

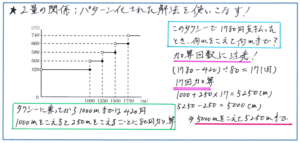
　そして、「2量の関係」では、「時刻のずれ」も要注意単元となります。比較対象となる正しい時刻とずれた時刻をわかりやすくかき出して、それぞれの進む速さの比を求めるという鉄則にしたがって、注意深く解答を進めるようにしましょう。この「時刻のずれ」の問題も今回のグノレブで出題される可能性が高くありますので、テキストの解説を熟読して、一連の解法の流れをしっかり覚え込んでおいてください。

【第4位　立体図形：展開図を利用した解き方は使いこなせていますか？】

　立体図形の中では、展開図を利用して解く問題にも注意が必要です。具体的には、テキスト【立体図形(1)】の2ページ目に出てくるような、「円すいの側面にそって引いた線が最短距離となる場合」や、「直方体の頂点を面にそって引いた線が最短距離となる場合」といった、「最短距離」に関連する問題が圧倒的に多くなります。

　円すいの展開図がおうぎ形と円の組み合わせになることや、直方体の展開図のパターンはすでに頭の中に入っていると思われますが、気をつけておきたいのが、作業を最小限におさえて、解答時間を短くすることです。

　例えば、直方体の面上を通る直線が出題対象となった場合であれば、直方体の展開図をすべてかく必要はなく、あくまで直線が通過する面のみで長方形を作図すればよいことになります。円すいでも、もちろん底面の円は必要なく（中心角も計算で求められます）、あくまで側面のおうぎ形のみで解き進められます。

　当たり前のように感じられるかもしれませんが、問題数が多いグノレブにおいて、この単元からの出題はテスト前半になると予想され、ここで時間を少しでも縮めることが、テスト全体の点数をアップさせるうえで重要な戦略となります。

　また、下の図のような四角すいの側面上を直線が通る場合も、全体の展開図の中から、該当する2つの三角形のみをかき出せば解答を進められます。立体の形が変わっても、最小限の展開図で解き進めることをいま一度強く意識しておきましょう。

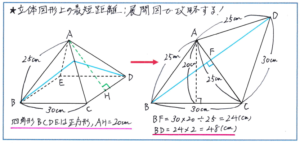
　今回のグノレブでは「立体図形」からの出題が多くなりますが、立体図形の問題を攻略するうえで作図は必須となります。それだけに、作図に時間をかけてしまうと、テスト全体の時間の使い方に支障をきたしてしまいます。いかにして作業を少なく、かつ解答に必要な情報を正確に得られるかを意識しながら、日々の演習を進めて行きましょう。それがそのまま有効な入試対策につながります。

【第5位　小数・分数：単位分数の和の解法の流れを確実に覚えられていますか？】

　小数・分数の単元からは、素因数分解を利用した問題が多く出され、特に「既約分数の和」の問題で、分数の並びを両端からたして行くという解法を正確に使いこなすなど、ここでもパターン化された解法をどれだけ理解できているかが試されます。

　その中のひとつが、「単位分数の和」の問題です。テキスト【小数・分数】では6ページ目に出てきますが、手間がかかるように見えても、解き方を固められていれば、着実に正解に向ってまい進することができます。一方で、解法を覚え込められていないと、解法に迷ったまま、結局は抜かす判断をしなければならないといった事態になってしまいます。

　単位分数の分子が1であることから、比較対象となる分数の分子を1とすべく、分母を計算するのですが、ここでの計算結果は整数で割り切れるケースはほとんどありませんので、小数・分数計算を正確に進めることがポイントとなります。

　あとは分数の大小関係を分母で見極めますので、分母が大きい程、分数は小さくなるといった基本中の基本の部分で間違わないように注意してください。言われるまでもないこととは思いますが、テスト会場では想定外に焦ってしまい、普段はしないようなミスをしてしまうことがあります。分数の大小関係もうっかり取り違えてしまうケースが多いので、普段からミスをしない意識を高めて演習を重ねましょう。

　今回のグノレブでは「立体図形」や、時刻のずれをはじめとした「2量の関係」で難問が出される可能性が高くあります。単位分数の和などの「小数・分数」の単元から得点源を少しでも多く確保できるように、自分がどの部分でミスしやすいか、といった誤答分析を徹底しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。