メールマガジン宝箱 Mail magazine

  5年生は「時計算」「流水算」「通過算」といった速さの問題、さらには「容器と水量」「ニュートン算」と、様々なタイプの重要単元がテスト範囲になります。共通する攻略ポイントは図を活用することです！図を使うことで、計算で求めた値が何を意味するのかが視覚的にとらえられるようになり、それが問題文のどこにポイントがあるのかを把握する大事なきっかけとなります！問題に応じてそれぞれの図のかき方をしっかり練習してください！

　4年生も場合の数や割合など、入試頻出の単元からの出題となります。場合の数では樹形図、割合では線分図と、内容を整理するために不可欠な図をいかに使いこなすかが勝負の分かれ目になります。テスト本番まで、とにかく図をかく練習を積み重ねてください。それが5年生以降に、問題を見て出題のポイントをつかむスピードに断然の差を生み出します！
　入試でも頻出の重要単元が範囲に含まれる組分けテスト！そこで今回は、ぜひ気をつけて頂きたいポイントを、5年生は第5位から第1位まで、4年生は第3位から第1位までのランキングのかたちにまとめました。ぜひクラスアップを実現してください！応援しています！
　さらに、このメルマガの5年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する攻略ポイントと予想問題を合わせれば、確固たる自信をもってテストに臨めます。予想問題はこちらのページで無料公開します！

《5年　第8回組分けテスト》

【第5位　時計算：長針と短針が1分間に進む角度を式で求められますか？】

　時計算で覚えておきたいものは「文字盤の数字と数字の間は1つ30度」「長針は1分間に6度回転する」「短針は1分間に1/2度回転する」の3つです。できれば丸暗記ではなく、数字を導く計算式も一緒に覚えておきましょう。入試では、8等分した時計(1日に3周する)や24等分した時計(1日に1周する)の出題も見られます。

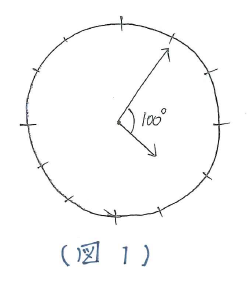
という問題を考えてみましょう。
　よくある間違いは、いつもの時計と同じだと考えて4時5分と答えることです。実際に4時5分のときの長針と短針の作る角度を計算すると、120－(6－1/2)×5＝92・1/2(度)となり(図1)と一致しません。この問題のポイントは、「短針は1時間に文字盤の数字1つ分しか回転しない」ということです。

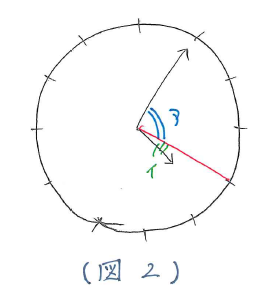
　したがって(図2)のように角度を分けると ア＝30×3＝90(度)、イ=100－90＝10(度)となり、短針は10度回転していることがわかります。このことから 10÷1/2＝20(分)経っていることがわかり、長針がさしている場所が文字盤の数字の4であることがわかります。よってこの時刻は7時20分だと求まります。
　このように一見変わった問題であっても、考え方の基本は先に挙げた3つになります。まずは時計の図をかいて、どの様な時刻かイメージを掴むことが大切です。繰り返し練習して身につけていきましょう。

【第4位　通過算：和差算の解き方は確実に覚えられていますか？】

　通過算の基本的な問題に「すれ違い」と「追い越し」があります。すれ違うときの公式は「列車の長さの和÷列車の速さの和＝すれ違いにかかる時間」、追い越すときの公式は「列車の長さの和÷列車の速さの差＝追い越しにかかる時間」です。この2つの公式を見比べてみると、「列車の長さの和」が両方の公式に入っていることがわかります。このことを利用すると次のような問題を解くことができます。
　「列車Aと列車Bが出会ってからすれ違い終わるまでに6秒かかりました。また、列車Aが列車Bに追いついてから追い越し終わるまでに24秒かかりました。列車Bの速さが時速60kmのとき、列車Aの速さは時速何kmですか。」
　この問題では列車の長さはわかりませんが問題を解くことができます。
　列車Aと列車Bの長さの和が一定なので、速さの比と時間の比が逆比になり、(列車の速さの和)：(列車の速さの差)＝1/6：1/24＝4：1＝8：2 となります。ここでは 4：1 ではなく 8：2 としておく方がいいでしょう。「和と差がわかる⇒和差算を使う」は見た瞬間に対応すべき必須のパターンです。そのため計算し易いように工夫をして 8：2 としたわけです。和差算より、列車Aの速さは (マル8＋マル2)÷2＝マル5、列車Bの速さは(マル8－マル2)÷2＝マル3 となります。マル3＝60(km/時)、マル1＝20(km/時)、マル5＝100(km/時)となり、列車Aの速さは時速100kmと求まります。
　このように列車の長さの和が一定であることを利用すると、速さの比と時間の比を上手く使うことができます。「すれ違い」と「追い越し」の問題では計算の省略にもなるので、解き方の一つとして身につけておきたいですね。

【第3位　容器と水量：簡単な問題で練習して面積図を徹底的に習得しましょう！】

　この単元が得意になるか苦手になるかは、面積図がかけるかどうかで決まります。複雑な問題になればなるほど、状況を図にまとめて考えることが要求されます。簡単な問題で図に状況をまとめる練習をして、応用問題でも図がかけるようにしていきましょう。

という問題で図のかき方を練習してみましょう。面積図はたてに「高さ(深さ)」、横に「底面積」をかき込みます。
　まず絶対にやってはいけないのは円周率を使うことです。計算がものすごいことになってしまいます。問題にあるからといって円周率を使う必要はありません。
　では何を使うかといえば比を使います。底面の円の相似比は (容器)：(棒)＝15：6＝5：2です。よって底面積の比は (容器)：(棒)＝(5×5)：(2×2)＝25：4 となります。

　はじめの状況を面積図に整理すると(図1)のようになります。比を使って水の量を表すと マル25×7＝マル175 となります。実際の水の量ではなく、比を使って水の量を決めることがポイントです。

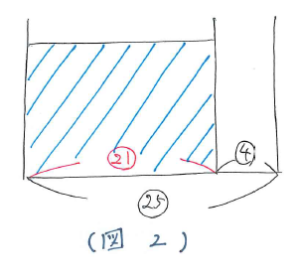
　次に棒を入れた後の状況を面積図に整理すると(図2)のようになります。容器の底面積をマル25、棒の底面積をマル4とかき込みますが、このとき棒の位置は左か右に寄せてかくようにします。すると水が入っている部分の底面積が マル25－マル4＝マル21 とわかるので、水の深さは マル175÷マル21＝8・1/3(cm)と求まります。
　　　

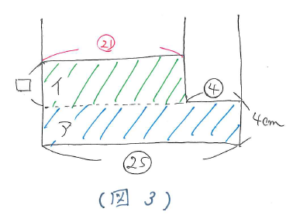
　最後に棒を引き上げたときの状況を面積図に整理すると(図3)のようになります。すると下から4cmは底面積がマル25の部分に水が入り、それより上では底面積がマル21の部分に水が入っていることがわかります。アの部分の水の量は マル25×4＝マル100 となるので、イの部分の水の量は マル175－マル100＝マル75 と計算できます。底面積がマル21なので、□＝マル75÷マル21＝3・4/7(cm) とわかります。したがって、水の深さは 4＋3・4/7＝7・4/7(cm) と求まります。
　このように基本的な問題で面積図のかき方を練習していけば、沈めるおもりが複雑になったり、おもりを複数沈めたり引き上げたりしても対応できるでしょう。繰り返し練習して確実に身につけていきましょう

【第2位　ニュートン算：内容を整理する線分図がかけていますか？】

　ニュートン算は苦手にしてしまうお子さんが多い単元の1つです。しかし、線分図をかくだけでかなり見通しが良くなります。しっかり線分図のかき方をマスターして苦手を得意に変えていきましょう。
　線分図のかき方ですが、まず線分図を1本かいて途中で区切ります。区切った左側の上の部分に「はじめの量」を書き、区切った右側の部分に「増加分」を書きます。線分図の下側全体に「減少分」を書き、これで完成(図1)です。実際に問題を解いて練習してみましょう。

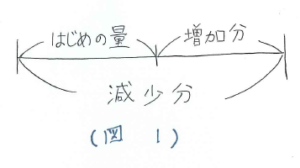
　ポンプ1台が1分間にくみ出す水の量をマル1とし、1分間にわき出る水の量をシカク1とします。シカク1がマル1の何倍なのかを求めるのが最初の方針です。
　わかっている状況が2つあるので線分図を2本たてに並べてかきます。このとき「はじめの量」をそろえてかき、「増加分」は90分水がわき出した2本目の方が長くなるようにかきます。すると線分図の長さに違いができるので、この部分の上に「増加分」の違いを、下に「減少分」の違いを書き込みます。上はシカク1×90－シカク1×45＝シカク1×45となり、下はマル1×5×90－マル1×8×45＝マル90となります(図2)。

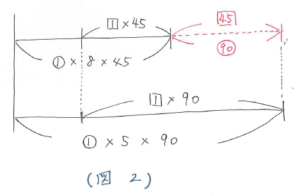
　よって、シカク1＝マル90÷45＝マル2と求まります。次に「はじめの量」がマル1の何倍なのかを求めます。1本目の線分図にシカク1＝マル2を代入して計算すると、はじめの量＝マル360－マル2×45＝マル270となります。最後にポンプ11台の場合を考えます。ポンプ11台が1分間にくみ出す水の量は、マル1×11＝マル11ですが、わき出る水の量が1分間にマル2なので、池全体としては マル11－マル2＝マル9 の水がくみ出されることになります。したがって、マル270÷マル9＝30(分)と求まります。
　このように線分図をかいてみると、計算して求められる箇所が目で見てわかるようになります。思考時間を大幅に減らすことができるので、線分図のかき方を身につけられるように練習を繰り返しましょう。

【第1位　流水算：逆比を正確に使いこなせることが攻略のポイントです！】

　流水算の応用問題では、今回学習した「静水時」「川の流れの速さ」「上りの速さ」「下りの速さ」の4つの速さの関係と、予習シリーズ5年下の第6回で学習した「道のりが一定のとき、速さの比と時間の比は逆比になる」という考え方が組み合わさった問題が多いです。このことに着目して問題を解いてみましょう。

　AB間の道のりは一定なので時間の比は 兄(上)：兄(下)：弟(下)＝40：20：30＝4：2：3となり、速さの比は兄(上)：兄(下)：弟(下)＝1/4：1/2：1/3＝3：6：4＝6：12：8 となります。川の流れの速さ＝(下りの速さ－上りの速さ)÷2 で求めるので、 川の流れが整数になるように 6：12：8 としておきます。川の流れの速さは (マル12－マル6)÷2＝マル3となります。したがって弟の上りの速さは マル8－マル3×2＝マル2と計算できます。また、AB間の道のりは比を使って マル6×40＝マル240 と決められます。よって弟が上るのにかかる時間は マル240÷マル2＝120(分)と求まります。
　流水算が苦手なお子さんは「流水算」が苦手なのではなく、それ以前の「速さの3公式」があやふやだったり、「速さと比」が上手く使えなかったりすることが多いです。シリーズ5年下第12回で速さの基本的な単元はすべて終わりました。これを機に速さの総復習をして、より理解を深めるようにしましょう。

【番外編　第6回から第9回の復習：あと一歩で得点できなかった問題を中心に復習を！】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第6回　速さと比　速さのつるかめ算
　・第7回　旅人算と比
　・第8回　影の問題　折り返しの相似
　・第9回　数表の問題

《4年　第8回組分けテスト》

【第3位　消去算：式の立て方を少し工夫すれば、代入法が使いやすくなります！】

　消去算で多くのお子さんが苦手としているのは、代入法を使う問題です。具体的には分配法則を使うときに、後ろの項にかけ忘れるミスが目立ちます。このミスは少し発想を変えるだけで解消できます。次の問題を使って考えてみましょう。

　まず普通に式をたてると、リ×5＋ミ×3＝590…(A)、リ×1＝ミ×3＋10…(B)となります。
　ここで(B)の式を(A)に代入して、(ミ×3＋10)×5＋ミ×3＝590 として分配法則を使うのではなく、(A)と(B)のリンゴを加減法のときと同じように最小公倍数にそろえるようにします。
　すると、リ×5＝ミ×15＋50…(B’)なり「ミ×15＋50」を(A)の式の「リ×5」と置き換えてミ×15＋50＋ミ×3＝590 ミ×18＝540 ミ×1＝30(円)となります。したがってリンゴ1個の値段は 30×3＋10＝100(円)と求まります。
　代入法が苦手であっても、加減法なら解けるというお子さんは非常に多いです。ですから代入法特有の解き方ではなく、加減法でも使った解き方に近づけることでミスを減らすことができます。また、式をしっかりかくこともミスを減らす方法です。繰り返し練習しましょう。

【第2位　場合の数：正しく場合分けができるように、問題文を丁寧に読みましょう！】

　この単元で差がつくところは、自分で場合分けして求める問題です。「偶数」や「5の倍数」を求めるときに、一の位に注目して場合分けをしていきましょう。

という問題で練習してみましょう。
　この問題では、一の位の数字が0、2、4のとき偶数になります。そこに注目して場合分けをしていきます。0が百の位の数になりえないことにも気をつけておきましょう。
(1) 一の位が0の場合
　百の位が1のときに、120、130、140の3通りあります。百の位が2、3、4のときも同じだけあるので、3×4＝12(通り)あります。
(2) 一の位が2の場合
　百の位が1のときに、102、132、142の3通りあります。百の位が3、4のときも同じだけあるので、3×3＝9(通り)あります。
(3) 一の位が4の場合
　(2)の場合と同じなので9通りです。
　したがって、12＋9×2＝30(通り)となります。
　また、書き出して調べる方法に、今回学習した樹形図があります。樹形図は慣れるまでは、曲がってしまって数え間違えたりします。樹形図は場合の数の基本です。ある程度曲がってしまうのは仕方がないですが、たてはそろえるようにしましょう。それだけでミスによる失点はかなり防げます。繰り返し練習して樹形図のかき方に慣れましょう。

【第1位　割合：線分図で、どの値がどの割合にあたるのかを把握しましょう！】

　お子さんが苦戦する問題の1つに「割合」「もとにする量」「くらべる量」が少し見つけにくい問題があります。このタイプの問題でもしっかり文章を読むことで解法の糸口が見つけられます。次の問題を考えてみましょう。

　状況を整理するために線分図を使います。まず、砂糖を使う前の線分図をかきます。線分図を途中で区切り、区切った左側をビンの重さ、右側を砂糖の重さとします。砂糖全体の重さを「もとにする量」として線分図の右側の下に「1」と書き込みます。また全体の重さが1100gなので、線分図の上側全体に1100gと書き込みます。次に使った後の線分図をかきます。ビンの重さは変わらないので、その部分をたてにそろえてかきます。砂糖を使ったあとの重さが560gなので、線分図の上側全体に560gと書き込みます。すると線分図の長さの違いが使った砂糖の部分だとわかります。ですからこの部分の下側に「3/5」と書き込みます。線分図を並べてみると、重さの違いが砂糖の重さの3/5だとわかります。したがって (1100－560)÷3/5＝900(g) と計算できます。これが砂糖全体の重さですから、ビンの重さは 1100－900＝200(g) と求まります。
　割合の問題では「くらべる量」÷「割合」で求められるのは「もとにする量」です。大事な式ですが、この式で求められた値が問題の答えになるとは限りません。最後まで気を抜かずに問題を解きましょう。

【番外編　第6回から第9回の復習：分数、小数の計算も十分に復習を！】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第6回　分配算　やりとりの問題
　・第7回　小数のかけ算、わり算　およその数
　・第8回　分数のたし算、ひき算
　・第9回　方陣算

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。