メールマガジン宝箱 Mail magazine

　今回のテストでは、30度60度90度の直角三角形の特質を利用して解く平面図形の問題や、等差数列の問題が多く出題される可能性が高いので、ズバリ偏差値アップのポイントは、まずは解法のパターンを丸暗記してしまうことです。次に、その解法の成り立ちまでを正確に理解することです。式の成り立ち（式が成立する過程）をしっかり理解しておけば、記憶に頼らなくても確実に正解に行き着けるようになります。そうした姿勢で算数に対峙し続けることは、自分で考える力を培い、初見の難問をも解ける力を一気に向上させ、結果として算数の偏差値を高く安定させることにつながるのです！
　これからご紹介する3つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題を合わせれば偏差値のジャンプアップを実現できます！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：30度・60度・90度の直角三角形の長さの比の意味を理解できていますか？】

　平面図形の中で、そのかたちの特性を利用することで、解ける問題の幅が一気に広がるものがあります。ここでご紹介する「30度・60度・90度で構成される直角三角形」はその代表格です。この図形の辺の長さの関係を活用できれば、図形の問題を解くスピード、正確さがこれまでとは別次元にまで向上します。下の左の図が基本形です。同じ図形を線対称の位置に置いて付けると正三角形になることから、最も長い辺（図のＡＢ）と最も短い辺（図のＢＣ）の長さの比が2：1となることがわかります。

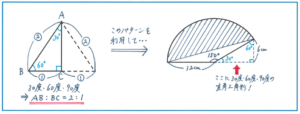
　この長さの比を活用すると、右の図のような中心角150度のおうぎ形の一部（斜線部）の面積も簡単に求められます。おうぎ形全体の面積から二等辺三角形の面積を引けば斜線部分の面積になりますので、以下の式から答えを導き出せるのです。
12×12×3.14×150/360―12×6÷2
＝188.4－36
＝152.4（平方cm）
　このような円の問題では半径の長さが同じであることを利用して、二等辺三角形と複合させたかたちで面積を求める問題が出されるケースがとても多く、例えば2017年度の慶應義塾普通部の最終問題で出題されたように、入試問題でもこの円にからめた30度60度90度の直角三角形のかたちが出題対象となる頻度は高いので注意しておきましょう。長さの比が2:1であることを確実に覚えておく必要がありますが、上記の左図のような図形の成り立ちを理解しておけば、どの辺の比であるかを忘れた場合にも、問題なく対応できます。辺の長さの比を丸暗記するのではなく、なぜその比になるのか、を必ず確かめておくようにしましょう。

【直前チェックポイント２：等差数列の和の公式について式の成り立ちを理解できていますか？】

　規則性の中で以下のような問題があります。

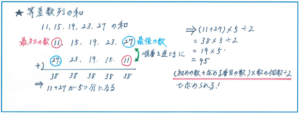
　まずは問題にある数の並びのきまりが、「11から始まり、数が4ずつ増える」ことに気づくのが大前提です。これから様々なタイプの数列の問題を解くことになりますが、まずは上記のような差が一定の「等差数列」であるかどうかからチェックする習慣をつけておくとよいでしょう。そのうえで、15番目までの和を求めるにあたり、「等差数列の和＝（初めの数＋求める番目の数）×数の個数÷2」の公式を確実に覚えて活用する必要があります。ただ、もしも公式を忘れてしまった場合には、上記のような図にすると、公式の成り立ちが説明できます。問題そのものを使ってもよいですが、時間を短縮させるには、例えば「11から23までの4個」と数を少なくして公式を確かめる方が楽でしょう。公式の成り立ちさえ思い出せれば後は計算になるので、記憶の掘り起しにかける時間はできるだけ短くしましょう。
　この問題では、15番目の数が、11＋4×(15－1)＝67なので、公式に当てはめて以下のように答えに行き着くことができます。
(11＋67)×15÷2＝585
　公式は使いこなせれば強力な武器となりますが、丸暗記して対応しようとするとほんの少しの記憶のほころびで正解を逃してしまうリスクもあります。公式を忘れないように、例えばゴロを使って唱えるのでもよいのですが、それよりも「なぜその公式になるのか？」といった原点に戻ることをぜひ優先されてください。式が成り立つまでの過程を確認することは理解を強固にするだけでなく、数に触れる機会を増やすことで数の感覚を研ぎ澄まし、さらには自分で考える習慣が身につく効果もあります。なぜ？の姿勢は算数の力をアップさせる要素となります。

【直前チェックポイント３：食塩水の問題では比の活用が効果的です！】

　ここまでは公式を丸暗記せずにその成り立ちから理解することの必要性について述べてきましたが、ここでは少し視点を変えて、食塩水の濃度の問題での比の活用についてご説明します。
　次のような問題にはどのように対応すればよいでしょう。

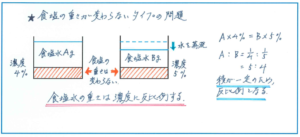
　問題の内容に合わせて、初めの食塩の重さを求める→その食塩が5%にあたる食塩水の重さを求める→初めの食塩水の重さとの差が蒸発させた水の重さにあたる、という流れで進めれば、解きづらい問題ではないでしょう。予想問題でも上記の解法で進めています。
　ここで比を使った別の解法をご紹介します。ポイントは食塩の重さが変わらないこと。水を蒸発させる前の食塩水の重さは200ｇとわかっていますが、ここではあえてＡｇとします。そして水を蒸発させた後の食塩水の重さをＢｇとすると、食塩の重さは以下のような式で表すことができます。
蒸発させる前…Ａ×4%
蒸発させた後…Ｂ×5%
この2つの式で表される食塩の重さは同じですので、以下の等式になります。
Ａ×4%＝Ｂ×5%
積（かけ算の答え）が一定になることから、食塩水の重さ（ＡとＢ）は、濃度（4%と5%）に反比例します。
Ａ：Ｂ＝1/4：1/5＝5：4　…★
となります。Ａが200ｇですので、Ｂは200×4/5＝160（ｇ）となり、蒸発させた水の重さは200－160＝40（ｇ）と求めることができます。
　このように、食塩水の濃度で水を蒸発させて食塩の重さが変わらないタイプの問題では、食塩水の重さが濃度に反比例することを利用すると計算が楽になるメリットがあります。今回の問題のように濃度が4%、5%といった計算しやすい場合は、無理の比を使う必要はありませんが、例えば32%が48%になった、といった場合には、0.32や0.48のかけ算が発生します。それが比を利用すれば、32：48＝2：3となることから、計算はだいぶ楽になるでしょう。
　必ずどちらかで解く、とはせずに解き方をいくつか持っておけば、問題に応じて解きやすい方法を選ぶことができます。また、比を利用した解き方を忘れてしまった場合には、★の式に戻れば式を立てられるようになるでしょう。ここでも今回のテーマである、解法を丸暗記しないことが当てはまるのです。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。