メールマガジン宝箱 Mail magazine

　今回のテストでの偏差値アップのポイントは、間違えたけれど授業での説明を聞いたり、テキストの解説を読めば理解ができた問題、つまりあと一歩で正解に行き着けた問題について、徹底的にくり返し解き直すことです。6年生の4月になると、テストでは応用問題が増えてきます。そうした問題の中で、解説を読めば理解できるような問題は、すでに習得している基本的な解法を組みあわせれば解けるものであったり、より慎重に取り組めば正解できたものであるケースが多くあります。そうした問題をひたすらくり返し解き、寝ていても解けるくらいにまで解法を吸収しておけば、応用問題で正解するため解答のプロセスを自分のものにすることができます。そしてそれが偏差値を跳ね上げるための強固な地盤づくりにつながるのです！
　これからご紹介する3つのポイントをしっかりおさえて、偏差値アップ、クラスアップを実現してください。応援しています！
さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題を合わせれば偏差値をこれまでにないステージにまで引き上げることができます！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：循環小数の周期を確実にとらえられていますか？】

　例えば、以下のような規則性の問題であれば、数字をグル―プ分けして答えまで行き着くことは難しくないでしょう。

　上記の数字の並びであれば、［1,5,3,7,8］の5つの数字が1つのグループになり、このグループがくり返し並んでいますので、100÷5＝20より、余りが発生しませんので100番目の数字はグループ最後の、8と求められます。
　ここで、8と1の間に「/」をかき込むことで、グループ分けが視覚的にもとらえられます。
　同じような考え方で次の問題に取り組んでみましょう。正確に「/」をかき込むことはできるでしょうか。なお、分数は「分子／分母」のかたちで表記します。

　9/7＝9÷7を筆算して、数字の並びを確かめるというシンプルな問題ではあるのですが、注意深く取り組まなければ足元をすくわれてしまいます。筆算の結果を見ると、9÷7の答えは以下のような数の並びになっていることがわかります。
　9÷7＝1.285714285714…
　小数第1位以下は285714という6個の数字の並びがこの順にくり返されていますので、小数第50位の数字は、50÷6＝8あまり2より、8となります。
　注意すべきは整数部分の1を循環に含めない判断ができるかどうか、という点です。最初にご紹介した規則性の問題では、最初の数字の1も含めてグループ分けをしました。それと同じように考えて、筆算の途中（小数第5位）に1が出てきた瞬間に「最初に戻ったからここまでがグループだ」と判断してしまうと正解に行き着けないのです。慎重に計算を続けて、数字の並び方の反復が確認できたところで「/」をかき込んで規則性を見出す、という流れを徹底しましょう。得点源にできる問題での失点は何としても避けたいところです。シンプルに見える問題でも慎重な取り組みを忘れないでください。

【直前チェックポイント２：場合の数で道順を求める問題で正確なかきこみができていますか？】

　場合の数では、道順を求める以下のような問題があります。

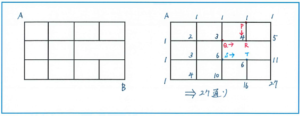
　このタイプの問題では、「カドに数字をかき込む」という解き方で進められれば正解に行き着けるのですが、ただ数字をかき込むとだけ丸覚えしてしまうと、右の図の点Ｒや点Ｔにどの数字をかき込めばよいのかがわからなくなってしまいがちです。かき込む数字はそこに行き着く道順が何通りあるかを表しています。点Ｒであれば、上の点Ｐからと左の点Ｑから行く道順がありますので、それを合わせて、1＋3＝4がかき込めます。一方の点Ｔですが、左の点Ｓからの道順はありますが、下から上ってくる道はまわり道になってしまいますので、こちらは含まれません。よって点Ｔに入る数字は6です。同じような位置にあっても算出の方法が異なりますので注意しましょう。
　このように、解き方がハッキリしている問題では解き方の丸覚えでは、少し出され方が変わっただけで対応ができなくなってしまいます。得点差がつきやすいタイプの問題ですので、根本的な理解をガッチリと固めておきましょう。

【直前チェックポイント３：速さと周期が合わさった問題に対応できていますか？】

　速さの問題の中で、線分図やグラフではなく、有効なかき出しをすることで正解に行き着けるタイプの問題があります。次の問題にはどのように対応すればよいでしょうか。

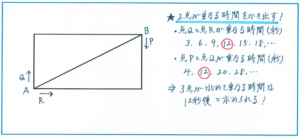
　点の移動のかたちをした旅人算の問題ですが、ただ2点どうしが向かい合った距離の72÷2＝36（cm）で出会う時間を求めても、そこから3点が出会う時間にどのように結びつければよいのかが、なかなか思い浮かばない問題です。かといってグラフを使える問題でもない。
　そこで、点Ｑと点Ｒが出会う時間の周期と、点Ｑが点Ｐに追いつく時間の周期を求めて、それを比べて、3点がはじめて同じ場所で重なる時間を求める方針で進めます。
　まず点Ｑと点Ｒが合わせて72cmの道のりを進むのには、72÷(14＋10)＝3（秒）かかります。ここからこの2点が3秒ごとに重なることがわかります。また、点Ｑがはじめて点Ｐに追いつくのは、72÷2÷(14－5)＝4（秒後）で、そこからは、72÷(14－5)＝8（秒）ごとに重なることをくり返します。
　点Ｑと点Ｒが重なる時間は、3秒、6秒、9秒、12秒、15秒、18秒、…
　点Ｐと点Ｑが重なる時間は、4秒、12秒、20秒、28秒、…
とかき出してみると、初めて3点が重なるのが12秒後であることがわかります。
　ここで点Ｐと点Ｒが重なる時間を求めても、72÷2÷(10＋5)＝2.4（秒後）から、72÷(10＋5)＝4.8（秒）ごとに2点が重なりますので、
　点Ｐと点Ｒが重なる時間は、2.4秒、7.2秒、12秒、16.8秒、…
となり、やはり12秒後が答えとなります。
　線分図もグラフも使えなくても、数字をかき出すことで攻略できる速さの問題があることを、しっかりおさえておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。