メールマガジン宝箱 Mail magazine

早稲田アカデミー・四谷大塚の皆様、新型コロナウィルス感染症対策のため、4/26の組分けテストは現在のところ実施されない予定ですが、今回のテスト範囲は6年生、5年生ともに大事な単元が目白押しです。テストがあると想定して、弱点を見つけ出し、その単元の重点演習をしっかりと重ねておきましょう！

6年生の皆様は、「速さと比」「立体図形」という、実際の入試でも大きな得点差が生まれる単元を確実に理解することがポイントです。どちらにも共通して必須となるのが、図をかくなど手を使って問題内容を正しく把握すること。速さと比では線分図やダイヤグラムを使えば問題内容が格段にわかりやすくなります。線分図はかき慣れておかないと、実際のテストの際にどれだけのスペースが必要になるかなど、意外なところで戸惑ってしまいがちです。はじめはゆっくりで構いませんので、自分で図をかく練習を重ねてください。立体図形では切断が範囲になります。以前までは上位校のみで出題されていた切断ですが、今では偏差値にかかわらず多くの学校で出題対象になっています。攻略のポイントは、切断面を自分の想像ではかくのではなく、正しい手順にそって進めること。手順さえつかんでおけば、難敵である切断を得点源にすることができます！

　5年生の皆様も「売買損益」「食塩水の濃度」といった割合の重要単元が範囲に含まれます。どちらも解答のパターンがはっきりとしていますが、基本となるところを確実におさえないままにパターンで解こうとすると、ミスを多発してしまいます。売買損益であれば売値や利益といった言葉の意味、食塩水の濃度であれば、濃度や食塩の量を求める基本公式を確実に理解してうえで、図を利用して式を立てる練習を重ねてください。特に食塩水の濃度で用いる面積図は、これから他の単元でも利用することがとても多い強力なアイテムです。これからの算数の偏差値アップの実現は、面積図のかき方をマスターできるかどうかにかかっていると言っても過言ではありません。とにかく繰り返し面積図をかく練習を重ねてください！

　今回の組分けテストは、今後の算数の偏差値を決定づける重要単元の出題が予定されていました。テストがなくてもしっかり振り返りをして、自分の復習ポイントを見つけておきたいところです。そこで今回は、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から6年生、5年生ともに第5位から第1位までのランキングのかたちにまとめました。ぜひ得点力アップを実現してください！応援しています！
　さらに、このメルマガの新6年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、入試最重要単元を理解する力が圧倒的にアップします。
予想問題はこちらのページで無料公開します！

≪6年　第2回組分けテスト≫

【第5位　旅人算と比：問題内容を線分図で整理できていますか？】

　速さの文章題では、条件をダイヤグラムや線分図等の図にまとめると一気に見通しがよくなることが多いです。問題文の内容をしっかりと把握する手助けにもなりますので、積極的に図をかいて問題を解く練習をしていきましょう。

という問題を考えてみます。
　まず、すれ違ったときを線分図に整理します。電車と電車の間隔をAB、電車と自転車がすれ違った地点をCとし、条件を線分図にまとめると(図1)のようになります。

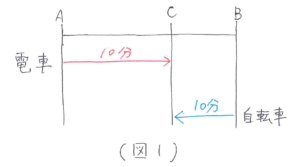
　次に、追い越したときを(図1)にかき加えます。電車が自転車を追い越した地点をDとし、条件を線分図にまとめると(図2)のようになります。

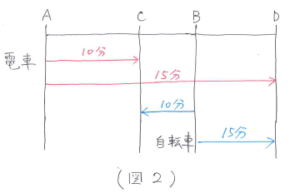
　ここでCD間に注目すると、電車は 15－10＝5(分)で移動し、自転車は10＋15＝25(分)で移動していることがわかります。(図3)

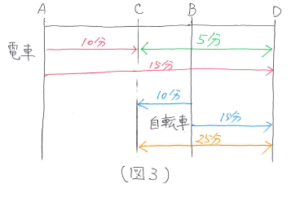
　したがって、時間の比が 電車：自転車＝5：25＝1：5 なので、速さの比は 電車：自転車＝5：1となります。速さの比を使って道のりを決めると、AB＝(5＋1)×10＝60 となり、電車の運転間隔は、60÷5＝12(分)と求まります。
　このように条件を図にまとめてみると、目で見て気が付くことができるようになります。ぜひ練習してみてください。

【第4位　回転体：立体の相似比を有効に活用できていますか？】

　相似な2つの立体図形には、「相似比が a：b のとき、体積比は (a×a×a)：(b×b×b) になる」という重要な性質があります。この性質を使うと回転体の体積が求めやすくなることが多いです。次の問題で練習してみましょう。

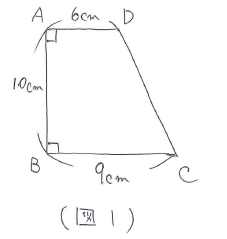
　辺BAの延長線と辺CDの延長線との交点をEとして、回転体をつくると(図2)のようになります。このとき、三角形EADと三角形EBCはピラミッド型の相似になっています。

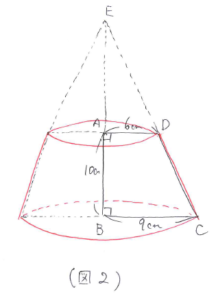
　相似比は、三角形EAD：三角形EBC＝6：9＝2：3 なので、EB＝30cmとなります。(図3)

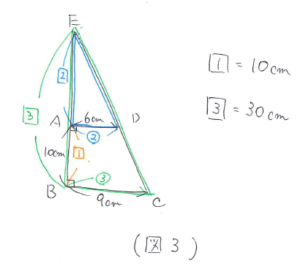
　また、小さい円すいと大きい円すいの相似比も2：3なので、体積比は (2×2×2)：(3×3×3)＝8：27 となり、大きい円すいから小さい円すいをひいた円すい台の体積は27－8＝19となります。
　したがって、求める回転体の体積は円すい台の体積になりますから 9×9×3.14×30×1/3×19/27＝570×3.14＝1789.8(立方cm)と求まります。
　この方法は回転体だけではなく、立方体を切断したときにできる立体にも応用できます。
　使えるようになると計算量をかなり減らせます。時間短縮にも、計算ミス防止にもなるので身につけておくと便利な解法の１つです。

【第3位　素因数分解の応用：解き方を理解できていないと手も足もでない問題です！】

　次の問題を考えてみましょう。

　この問題のポイントは、24＝2×2×2×3 なので「24で割る」＝「2で3回割って、3で1回割る」という点です。24の倍数を探さないように注意しましょう。たとえば、1×2×3×4＝24 です。1から4の中に24の倍数はありませんが、1から4までの整数の積は24で割り切れることがわかります。
　Aを素因数分解したときに、2が何個あるかを考えます。N進法の考え方を使って100÷2＝50、50÷2＝25、25÷2＝12…1、12÷2＝6、6÷2＝3、3÷2＝1…1 より、50＋25＋12＋6＋3＋1＝97(個)とわかります。このことから「2×2×2」は97÷3＝32…1 より32組作れることがわかります。
　次に、Aを素因数分解したときに、3が何個あるかを考えます。100÷3＝33…1、33÷3＝11、11÷3＝3…2、3÷3＝1 より、33＋11＋3＋1＝48(個) とわかります。
　以上の事から「2×2×2」が32組、「3」が48個あるので、Aは24で32回割れることがわかります。この問題では割り切れなくなる回数を問われているので 32＋1＝33(回目)と求まります。
　このような「典型的な問題＋α」をしっかり考えられるようになると、実力がぐんぐん伸び始めます。はじめは難しくても繰り返すことが重要です。頑張って取り組んでいきましょう。

【第2位　立方体の切断：自分の想像で図をかかず、正しい手順で進めましょう！】

　立方体の切断は手順を守って解けば必ず解けます。自分の想像で切り口の図形の辺をかかないように注意しましょう。

　順を追って考えていきましょう。
(1) 同一平面上の切り口の平面が通る点は直接結べるので、AとP、AとQをそれぞれ結びます。(図1)
　　

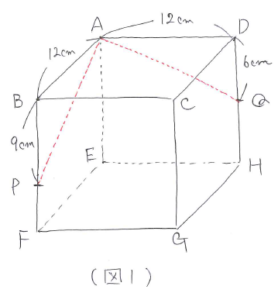
(2)　平行な面にある切り口の図形の辺は必ず平行になります。具体的には、三角形ADQと三角形RFP、三角形ABPと三角形SHQがそれぞれ相似になります。

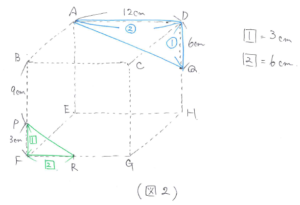
(3)　三角形ADQと三角形RFPの相似(図2)から、AD：DQ＝12：6＝2：1 より、RF：FP＝2：1 となるので、FR＝(12－9)×2＝6(cm)と求まります。

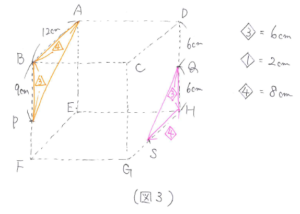
(4)　三角形ABPと三角形SHQの相似(図3)から、AB：BP＝12：9＝4：3 より、SH：HQ＝4：3となるので、SH＝(12－6)×4/3＝8(cm)となります。よってGS＝12－8＝4(cm)と求まります。

　このようにわかるところから順番に求めていきます。切り口の図形の辺を一筆書きしようとして、自分勝手にかかないように注意しましょう。立方体の切断はこの後の立体の切断にもつながっていきますので、1問1問丁寧に問題に取り組んで確実に解けるようになるまで練習しましょう。

【第1位　速さと比：問題文から長さの関係などを的確に把握できていますか？】

　次の問題を考えてみましょう。

　条件を整理します。行きは、AB間が上りになり、BC間が下りになります。反対に、帰りは、AB間が下りになり、BC間が上りになります。かかった時間の違いから、行きの方が帰りと比べて、上っていた時間が長いことがわかります。つまり、AB間とBC間ではAB間の方が長いことがわかります。

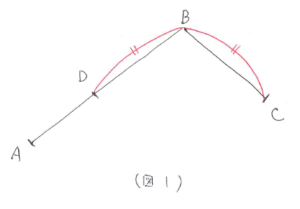
　AB間に(図1)のようなBD＝BCとなるD地点を考えます。DC間では行きと帰りにかかる時間が等しくなるので、行きと帰りにかかる全体の時間の違いはAD間にかかる上りと下りの時間の違いになります。
　　
　まずAD間で考えると、速さの比は 上り：下り＝3：6＝1：2 なので時間の比は 上り：下り＝2：１です。マル1＝5－4＝1(時間) となり、DからAまで下るのに1時間とわかるので、AD＝6×1＝6(km)と求まります。
　次にDC間を考えます。行きで考えると、DC間にかかる時間は 5－1×2＝3(時間) 、DB間が上りで、BC間が下りなので、時間の比は DB：BC＝2：1 となります。したがってDB間にかかる時間は、3×2/3＝2(時間)となり、DB＝3×2＝6(km) となります。
　よってAB＝6＋6＝12(km)と求まります。
　条件を整理してABの方が長いことに気付かないと解くのに苦労する問題です。1つの問題の中で考えることが多い問題ですが、筋道を立てて考えられるように練習しましょう。

【番外編　第1回から第4回までの復習：N進法の解法を覚えていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」ということが無いようにしましょう。特に確認したいものは以下の通りです。
　・第1回　やりとり算、いもづる算、差集め算
　・第2回　周期算、曜日、N進法
　・第3回　角度、面積と辺の比、正六角形
　・第4回　道順の利用、図形と場合の数

≪5年　第2回組分けテスト≫

【第5位　利益と損失：マル1など数を記号化すると一気に解きやすくなります！】

　仕入れ値がわからない問題は、仕入れ値をマル1(割合)として考えると上手くいくことが多いです。次の問題で練習してみましょう。

　仕入れ値をマル1とすると、定価＝マル1×(1＋0.5)＝マル1.5、売り値＝マル1.5×(1－0.3)＝マル1.05、利益＝マル1.05－マル1＝マル0.05 となります。
　実際の利益は200円なので、マル0.05＝200(円)となり、マル1＝200÷0.05＝4000(円)と求まります。
　このタイプの問題は非常によく出題されます。必ず解けるようにしましょう。

【第4位　食塩水の面積図：面積図のかき方の基本を徹底的に覚え込みましょう！】

　食塩水の問題は、「食塩水の濃さ＝食塩の重さ÷食塩水の重さ」「食塩の重さ＝食塩水の重さ×食塩水の濃さ」「食塩水の重さ＝食塩の重さ÷食塩水の濃さ」の3つの公式を使って求めていきますが、これらの公式が使いづらい問題があります。そのときに便利なのが、たてを「食塩水の濃さ」、横を「食塩水の重さ」、面積を「食塩の重さ」にした面積図(図1)です。
　　　　　　

　この面積図は第2回で学習した「平均の面積図」と同じもので、使う名称だけ食塩水の公式に直したものになります。したがって使い方も平均の面積図と同じです。
　次の例題で試してみましょう。

　まず横長の長方形をかき、たてに「食塩水の濃さ」の12％、横に「食塩水の重さ」の100gと書き込みます。次に今かいた長方形の横にくっつけてもう1つ縦長の長方形をかき、たてに「食塩水の濃さ」の100％、横に「食塩水の重さ」の□ｇと書き込みます。(図2)

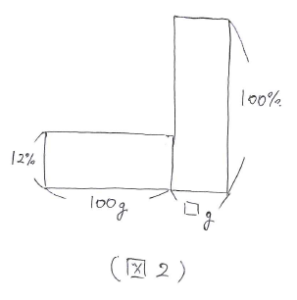
　ここで注意することは、「食塩水＝食塩＋水」なので食塩は100％の食塩水として(余談ですが、水は0％の食塩水として)計算します。また、食塩水の重さ＝食塩の重さになります。
　次に混ぜると20％になっているので、12％と100％の間のところに左から右まで点線をかきこみ、点線から長方形の下の辺までの長さに10％と書き込みます。このとき(図3)の面積図のアの部分とイの部分の面積が等しくなるので、(1－0.2)×□＝(0.2－0.12)×100、□＝10(g)と求まります。
　　　
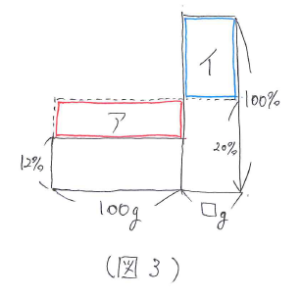
　食塩水の面積図は5年生の後半で「比」を学習すると、さらに簡単に解けるようになります。この機会に身につけておきたい解き方です。

【第3位　複数個の品物の売買：つるかめ算の考え方を使いこなせていますか？】
　

　複数個の品物を売買する問題では、品物を値引きして仕入れ値より安く売ったり、品物が売れ残ったりすることがあります。そのため利益はお店全体で考えなくてはなりません。したがって、「売り上げの合計－仕入れの合計＝利益」として計算します。

という問題を考えてみましょう。
　まず1個あたりの売り値を考えます。定価は200×(1＋0.2)＝240(円)となり、値引き後の売り値は240×(1－0.3)＝168(円)となります。次に仕入れの合計ですがこれは、200×100＝20000(円)です。利益は2920円とわかっているので、売り上げの合計は20000＋2920＝22920(円)となります。
　ここまでの事を整理すると、「1個240円の品物と1個168円の品物を合わせて100個売ると、売り上げが22920円になりました。240円の品物は何個売りましたか。」という問題になります。個数の合計と売り上げの合計がわかっていて、それを240円で売った個数と168円で売った個数にわけるので、「つるかめ算」ですね。
　よって、定価で売った品物の個数は (22920－168×100)÷(240－168)＝85(個)と求まります。
　この問題では値引き後に利益がでないので、売り上げを使ったつるかめ算にしましたが、値引き後の値段でも利益が出ているときは、利益だけを使ったつるかめ算で求めることもできます。

【第2位　円：半径の長さがわかっていなくても面積を求める方法があります！】

　円の面積は、「半径×半径×円周率」で求まります。半径がわかっていればすぐに計算できますが、半径がわからないときはどうすればいいでしょう。半径がわからないときは、「半径×半径」の値を考えると解くことができます。もちろん小学生はルートの計算は出来ないので、正方形や直角二等辺三角形の面積を利用して求めます。

という問題を考えてみましょう。
　　　　

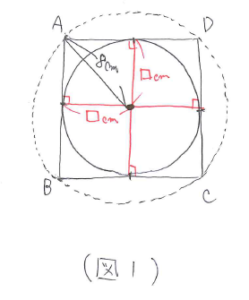
　まず円Oの面積ですが、これは8×8×3.14＝64×3.14となります。ここで気をつけたいのは「最後まで計算しない」ということです。円Qの面積を求めるときも円周率を使うので、3.14の計算は後でまとめて計算します。
　次に円Qの面積ですが半径がわかりません。したがって「半径×半径」を求めることにします。円やおうぎ形の問題では、半径を補助線として引くと見通しが良くなることが多いです。今回も補助線として円Qの中心から、正方形ABCDと円Qの4つの接点に向かって半径を4本引きます。すると、(図1)のように正方形ABCDを4つに分けた小さい正方形が４つ出来ます。その小さい正方形を見てみると、1辺が円Qの半径と同じで対角線の長さが8cmになっていることが分かります。このことを利用して「半径×半径」をもとめます。円Qの半径を□とすると、□×□＝8×8÷2＝32 となるので円Qの面積は32×3.14となります。
　最後に何倍かを計算します。(64×3,14)÷(32×3.14)＝2(倍)と求まります。
　このように応用問題では半径がわからないことが多いです。そのときは「半径×半径」が求まるはずだと考えて解いていきましょう。また、3.14の計算は最後にまとめて計算するくせをつけましょう。計算のスピードが上がりますし、なによりミスが激減します。繰り返し練習して身につけましょう。

【第1位　取り違えの問題：図をかいて内容を整理すると圧倒的に解きやすくなります！】
　

　差集め算では問題文の中から、「全体の差」「1つあたりの差」「個数」という要素を探して考えていくことが基本になります。問題文を読むときにこれらの要素を意識しながら読んでいくと問題を解く手がかりになるでしょう。

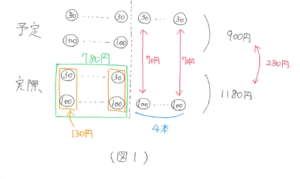
　この問題のポイントは、金額の違いは本数の違いによって発生するということです。このことから鉛筆とボールペンの本数の差は、(1180－900)÷(100－30)＝4(本)とわかります。また、問題文から安い方(鉛筆)を多く買う予定が高い方(ボールペン)を多く買ってしまったため代金が増えてしまったと読み取れます。実際に買った本数はボールペンの方が4本多いので鉛筆の本数にそろえると代金の合計は 1180－100×4＝780(円)となります。ここで鉛筆とボールペンの本数がそろったので鉛筆1本とボールペン1本を1組として考えるのが上手いやり方で、その結果、鉛筆とボールペンの組が780÷(30＋100)＝6(組)できることがわかります。これは実際に買った鉛筆の本数と等しいですから答えは6本と求まります。
　このように見た目は異なりますが、問題を解く鍵は最初に挙げた3つの要素になります。
　また、問題文を読んでもわかりにくいときは、(図1)のような図をかいてみるのも理解の手助けになります。繰り返し練習して１つずつ確実にできるようにしていきましょう。

【番外編　第1回から第4回までの復習：面積図、線分図のかき方を復習しましょう！】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第1回　約数、倍数、等差数列
　・第2回　平均の面積図、つるかめ算
　・第3回　N角形の公式、三角定規の三角形
　・第4回　割合の3公式、相当算の線分図

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。