メールマガジン宝箱 Mail magazine

　今回のテストでの偏差値アップのポイントは、図を用いて比の関係を把握することです。相当算であれば、まずは線分図をたてにかき並べる典型のパターンを行ったうえで、わかっている数値を線分図にかき込む。ここまでは、これまで学習した内容で対応できますので間違いなく実践したうえで、線分図から比の関係を読み取ることが6年生のテストならではの対策となります！線分図の長さとかき込んだ数値をよく見て、比の関係をつかみとれれば、スムーズに式を立てることができ、一気に正解に近づけます。食塩水の濃度や速さの問題でも同じことです。これまで習った図のかき方を駆使して、そこから比の関係を見つけ出す流れをしっかり身につけて、得点力をこれまで見たことのないレベルにまで跳ね上げましょう！
　これからご紹介する3つのポイントをしっかりおさえて、得点力のジャンプアップを実現してください。応援しています！　　
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題を合わせればこれまでにない正答数をたたき出せます！
予想問題はこちらのページで無料公開します！

【直前チェックポイント1：濃度がわかっていない食塩水の混ぜ合わせに対応できていますか？】

　2つの食塩水の混ぜ合わせる問題で、例えば、「濃度が16%の食塩水800gと、濃度が10%の食塩水400gを混ぜ合わせる」といった濃度がわかっている問題であれば、計算でも面積図を使っても正解に向かう道すじを作ることはできるでしょう。それでは、以下のような問題ではいかがでしょう。

　予想問題では、図を使わずに数値の大きさを調整して、式と計算のみで解く方法を詳しく解説していますので、ぜひそちらも参考にしてください。ここではその解法が思いつかない場合に、図を使って解く方法をご紹介します。
　ポイントは混ぜ合わせてできる2つの食塩水の重さが同じであることです。そこで次のような2つの図をかくことができます。これは天びん図を利用した図ですが、食塩水の重さの比と濃度の差（混ぜ合わせてできた濃度と、もとの濃度の差）の比が逆比の関係になる考え方は、面積図のかき方でも演習した内容です。

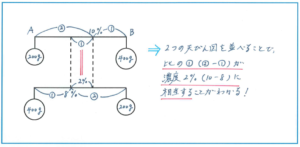
　上の図のように、濃度の差の比が2：1の場合は10%に、濃度の差の比が1：2の場合は8%となります。Ａの濃度とＢの濃度の差、ＡとＢの合計が600gで等しいことから、比の値を同じと考えられるので、上の①の長さが、10－8＝2（%）にあたることがわかります。よって、Ａの濃度は10－2×2＝6(%)と求められます（Ｂの濃度は10＋2×1＝12（%）になります）。
　面積図をかけなくても、その一部を利用した図をかけば正解に行き着くための式を立てることができるのです。ぜひ図の幅広い使い方を習得しましょう。

【直前チェックポイント2：相当算の線分図を正確にかけていますか？】

　相当算では、線分図をかいて問題内容を整理する必要があります。問題文が長く複雑に見える問題でも、線分図を正確にかくことができれば、式をスムーズに立てることができるようになります。次の問題で線分図のかき方を確かめてみましょう。なお、メルマガでは分数を、分子/分母のかたちで表します。

　この問題内容を線分図で整理すると以下のようになります。

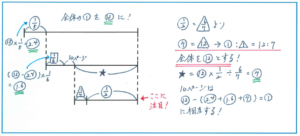
　ポイントは元にする量が変化すること。2日目と3日目は前の日に読んだ残りが全体の量となるので、図のように割合を表す記号を変えることに注意しましょう。また、線と線の間を狭くしてしまうと、数値をかき込みづらく、無理にかき込んでも見えづらい図になってしまいます。ただ、逆に幅をとりすぎてかく習慣がついてしまうと、テストの際に空いたスペースにかききれなくなってしまいます。自分が読み取れる範囲内で小さく数値をかき込んで図を完成できるように練習を重ねましょう。
　この問題では、上から3本目の線分図に解法のきっかけを見つけ出します。全体の1/2と3日目の残りの6/7が等しいことから、全部のページ数と、3日目の残りのページ数を比で表すと12：7になります。そこから全部のページ数をマル12、3日目の残りのページ数をマル7とすることで、10ページがマル12－(マル2.4＋マル1.6＋マル7)＝マル1にあたるので、本全部のページ数を、10÷1×12＝120(ページ)と求めることができます。
　3本目の線分図から逆比の考え方でページ数を比で表す点に難しさはありますが、線分図を正しくかくことで解法の筋道を立てることができます。

【直前チェックポイント3：場合の数で「当てはまらない数を引く」の応用型を使えていますか？】

　比を使う問題ではありませんが、場合の数でぜひご紹介したい解き方があります。以下のような問題です。

　この問題のような数字を並べる問題で0のカードが含まれると、いつも0の扱いに手を焼きます。3けたの整数であれば、0を百の位、十の位におくことができないことに気をつけなければなりません。
　さらにこの問題ならではの難しさは「同じカードが2枚ずつ」であるという点です。例えば3のカードに注目すると、百の位と十の位で3を使うと、一の位では3のカードが使えなくなるのです。0の扱いだけでも大変なところ、さらに使えないカードが出てくることに気を配らなくてはなりません。
　やり方の工夫なしに解く場合には、0のカードの枚数で場合分けをしますが、0のカードを1枚も使わない場合にも、同じカードを2枚使う場合と、すべて異なるカードで数をつくる場合に、また分けて考えなくてはなりません。場合の数を苦手とする生徒さんの多くが、この場合分けに難しさを感じることが多くあります。
　そこでここでは、問題の条件を変えて、仮のかたちで場合の数を出し、そこから条件に合わないものを引く、という解法で進めてみます。
　少しわかりづらいかと思いますが、具体的には、「同じカードが3枚ずつある」と仮定するのです。同じカードが1枚ずつ増えただけで解きやすさが全く変わってきます。カードが3枚ずつあれば、百の位に1から4の4通り、十の位には0から4の5通り、一の位も0から4の5通りの数が使えますので、4×5×5＝100（通り）の整数が作れることになります。
　ここからがポイントですが、カードが3枚ずつあった場合には作ることができて、2枚ずつでは作れない3けたの整数は「111、222、333、444」の4個しかないのです。この4個を引いた、100－4＝96（個）が答えとなります。
　式の数も圧倒的に少なく、何より場合分けが必要ない点で、速く正確に解ける方法です。仮の条件に想定するというのはレベルの高い切り口ですが、「このかたちだったら解きやすいのに」と試行錯誤する習慣があれば、思いつくことは決して困難ではありません。そのためには、「このかたち」に該当する、場合の数の基本的な解法を少しでも多く習得しておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。