メールマガジン宝箱 Mail magazine

　6月にもなると組分けテストの難度も高くなり、どこから復習すればよいのかがわかりづらくなります。そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から6年生、5年生ともに第5位から第1位までのランキングのかたちにまとめました。メルマガを読んで、ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このメルマガの6年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、偏差値アップを一気にたぐりよせることができます！頑張りましょう！
予想問題はこちらのページで無料公開します！

≪6年　第3回組分けテスト≫

　6年生は、「点の移動」や「食塩水の濃度」「ニュートン算」といった、量の変化がテーマとなる単元が主な範囲となります。「点の移動」では、時間の変化によって面積がどのように変わっていくのか、「食塩水の濃度」の食塩水を一定量やりとりさせる問題では、濃度が段階を追ってどのように変化するのか、その様子を正確に把握する力が求められます。こうした変化がテーマとなる問題で確実に得点するためには、図をかいて内容を整理する作業が断然の効果を生み出します！食塩水の問題であればビーカー図や面積図、ニュートン算や相当算では線分図と、問題のパターンに応じてどの図をかくのかが瞬時に頭に浮かぶように練習を重ねておけば、速く正確に難問を解き進めることができるようになります！

【第5位　相当算：マルやシカクを使った割合の記号化はできていますか？】

　まずはウォーミングアップから。

　線分図にまとめて解いていくと、図1のようになります。

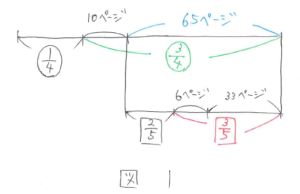
(6＋33)÷(1－2/5)＝65(ページ)
………シカク1あたり
(10＋65)÷(1－1/4)＝100(ページ)
………マル1あたり
よって、100ページと求まります。
　この問題と似ていますが苦手とするお子さんが多い問題で、最後に割合が残る問題があります。計算は少し複雑になりますが、考え方の道筋は同じです。前の問題と比較しながら解いてみましょう。

　線分図にまとめると図2のようになります。同じように解いてみましょう。

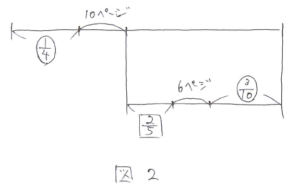
　(6＋マル3/10)÷(1－2/5)＝10＋マル1/2(ページ)
………シカク1あたり
　分配法則を使って解くとこのようになりました。(図3)

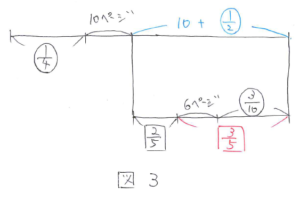
　図3から、マル1/4＋10＋10＋マル1/2＝マル1とわかり、これを整理して マル1/4＝20、マル1＝80 となり、80ページと求まります。
　このように、似ている問題は似たような解き方を使えることがあります。典型的な問題の考え方は応用問題の土台になっていることが多いので、積極的に練習して身につけていきましょう。

【第4位　既約分数：和を求める問題では、分数の並び方に注目しましょう！】

　次の問題はシンプルですが、解き方を知らないと苦労する問題です。確認してみましょう。

　216を素因数分解すると、216＝2×2×2×3×3×3　となるので、分子が2の倍数または3の倍数のときに約分できてしまいます。既約分数は、全体から約分できる分数を除けば求まります。
　215÷2＝107…1、215÷3＝71…2、215÷6＝35…5　となるので、約分できる分数は、107＋71－35＝143(個)となります。したがって既約分数は215－143＝72(個)と求まります。
　次に既約分数の和を考えます。具体的に分数を並べてみると
　1/216、5/216、7/216、11/216、………、205/216、209/216、211/216、215/216
となっています。これらの既約分数をよく見ると、「前から1番目と後ろから1番目の和」、「前から2番目と後ろから2番目の和」、「前から3番目と後ろから3番目の和」、………
とすべて1になっています。全部で72個の既約分数があるので　和が1となる2つの分数の組を72÷2＝36(組) 作ることができるので、1×36＝36と既約分数の和が求まります。
　分母が小さいときは書き出すこともできますが、大きくなると計算で求めないと時間がかかってしまいます。この時間の差が点数の差にもつながってきますので、順序良く解けるように練習しましょう。

【第3位　食塩水のやりとり：図を使ってやりとりの流れを正確に追えていますか？】

　やりとりの問題は丁寧に順を追って図をかいていきます。食塩水でも例外ではありません。必要なもの(濃さ、食塩、食塩水)がわかるようにしっかりとかいていきましょう。

　という問題を解いてみましょう。難しそうな問題ですが、発想を変えると一気に解けてしまいます。
　等しい濃さをX%として、やりとりの図をかくと図1のようになります。

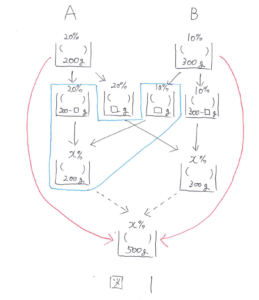
　ここで、問題文にはありませんがAの容器の食塩水とBの容器の食塩水を混ぜる(図1の点線)とX%の食塩水が500gできることになります。これは、はじめの食塩水を全部混ぜたものと同じになります(図1の赤い矢印)。このことからX＝(200×0.2＋300×0.1)÷(200＋300)×100＝14(%)となります。
　次にAの容器で考えて(図1の青い囲み)面積図をかきます。20%の食塩水と10%の食塩水をまぜて、14%の食塩水が200gできたという面積図(図2)がかけます。
　

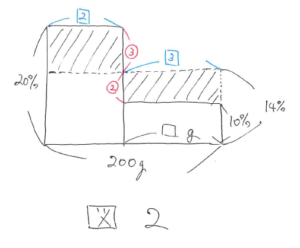
　面積が等しい部分の長方形のたての比が、(左の長方形)：(右の長方形)＝(20－14)：(14－10)＝3：2　となるので長方形の横の長さの比は、(左の長方形)：(右の長方形)＝1/3：1/2＝2：3　となります。よってBから取り出した食塩水の量は、200×3/5＝120(g)と求まります。
　ひとりでは気付き難い問題なので、一度解いたことがある人とない人で問題から受ける難易度が変わり、テストのときの対応が分かれる問題です。言い換えれば、他の受験生に差をつけることができる問題ともいえます。ぜひ身につけておきましょう。

【第2位　ニュートン算：ニュートン算ならではの線分図のかき方を習得しましょう！】

　ニュートン算は条件を目で見てわかるように線分図にまとめると解き易くなります。
　よく問題で取り上げられるのは、「ポンプで水をくみ出す」「窓口に人が並ぶ」「牛が草を食べる」というパターンです。これらの問題を図1のような線分図をかいてまとめていきます。

という問題で練習してみましょう。

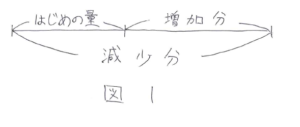
　図1を参考に問題の条件に合うように線分図をかいていきます。
　牛1頭が1日に食べる草の量をマル1とし、1日に生えてくる草の量をシカクとします。2つの条件を並べてかくと、図2のようになります。

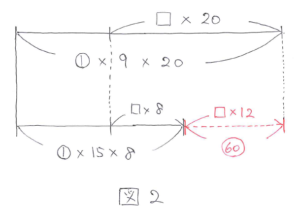
　シカクがマル1の何倍なのかを求めるのが最初の方針です。線分図の右側の違いから、シカク×12＝マル60とわかり、シカク＝マル5とわかります。
　次にはじめの量を求めます。上の線分図で、シカク＝マル5を代入して、マル180－マル5×20＝マル80 とわかります。
　このことから、牛25頭を放牧すると草は、マル80÷(マル1×25－マル5)＝4(日) でなくなると求まります。
　ニュートン算の典型的な問題はこのように線分図を使ってあっさりと解くことができます。思考時間を大幅に減らせるので、ぜひ身につけてください。

【第1位　点の移動：相似の考え方を使った解き方を使いこなせていますか？】

　次の問題を考えてみましょう。

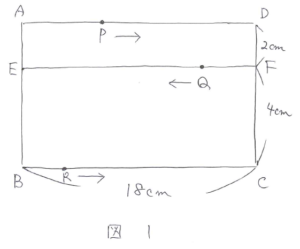
　架空の移動する点を作る解き方もありますが、図形的に解く解き方で考えてみたいと思います。
　3点が一直線になる時間をマル1秒後とします。このときPは 5×マル1＝マル5(cm)、Qは 3×マル1＝マル3(cm)、Rは　2×マル1＝マル2(cm)、それぞれ動いたことになります。また、RからABに平行な線を引きEFとの交点をG、ADとの交点をHとすると、図2のようになります。

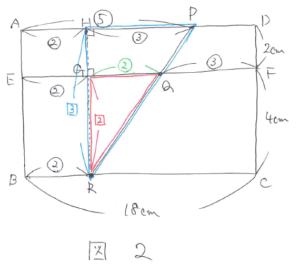
　このとき、三角形RQGと三角形RPHはピラミッド型の相似になっていて、相似比はRG：RH＝4：(4＋2)＝2：3 となります。このことからGQ＝(マル5－マル2)×2/3＝マル2 とわかりEF＝マル2＋マル2＋マル3＝マル7になります。したがって、
マル7＝18、マル1＝2・4/7　となり2・4/7秒後と求まります。
　(注) 厳密には、マル7＝18cm、マル1＝18/7cm、AR＝18/7×5＝90/７cm、よって、
　90/7cm÷5cm/秒＝2・4/7秒後 と求めます。
　ここで植木算の「池の周りに木を植える」パターンを思い出してください。このと
　　き「木の本数＝間の数」ですから、単位は「本」と「ヶ所」で違いますが数字は同じなので、計算にはそのまま使うことができました。
　これと同じように考えて、単位は「cm」と「秒後」で違いますが、数字は同じになるので、マル1が求まればそのまま答えても大丈夫です。気になるようでしたら、解説のように単位をつけずに数字だけ求めるといいでしょう。

【番外編　第6回から8回の復習：立方体の切断面のかたちを正確に区別できていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第6回　立方体の切断、回転体
　・第7回　素因数分解の応用、わり算と余り
　・第8回　旅人算と比、ダイヤグラム

≪5年　第3回組分けテスト≫

　5年生は「場合の数」から、道順や色のぬり分け、並べ方と組合せの混合型の問題など、難度の高い単元がテスト範囲に含まれます。場合の数を苦手とする生徒さんの多くは、こうした単元で得点力が下がってしまったことがきっかけで、苦手意識を強く持っていると考えられます。場合の数の難問で正解を増やすためには、やり方をただ丸暗記しないこと！道順であれば、角（カド）に入る数は何を意味しているのか、ぬり分けの問題ではどのように場合分けをすれば、式が立てやすくなるのか、といった正解に至る流れを都度確認するようにしましょう。確かな根拠を持って式がかければ、場合の数を得点源にするチャンスが生まれます。それは得点力で大きな差を生み出すことにつながります。

【第5位　回転体：回転してできる立体の見取り図のかき方は理解できていますか？】

　回転体を考える上で大切なのは、図をかいてどのような立体になるかイメージを持つことです。テスト等では、問題にかいてある図に少し手を加えるだけで求めたい立体の形が出来上がります。次の問題で練習してみましょう。

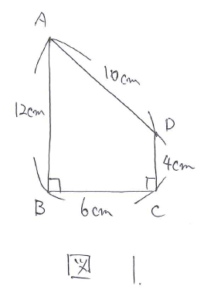
　まずPの図をかいて、それを基に体積と表面積を計算します(図2)。

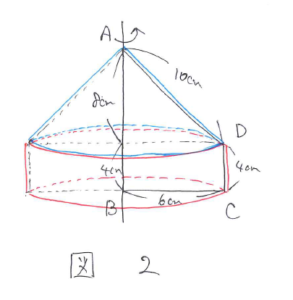
　体積は、6×6×3.14×4＋6×6×3.14×8×1/3＝(144＋96)×3.14＝240×3.14となり、表面積は、6×6×3.14＋6×2×3.14×4＋10×6×3.14＝(36＋48＋60)×3.14＝144×3.14となります。まだ計算が続くので3.14の部分は計算しません。
　

次にQの図をかいて、それを基に体積と表面積を計算します(図3)

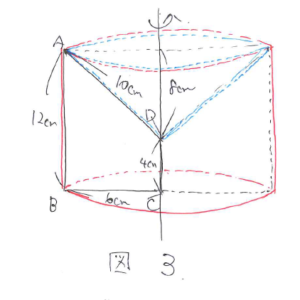
　体積は、6×6×3.14×12－6×6×3.14×8×1/3＝(432－96)×3.14＝336×3.14となり、表面積は、6×6×3.14＋6×2×3.14×12＋10×6×3.14＝(36＋144＋60)×3.14＝240×3.14となります。
　したがって、体積の差は336×3.14－240×3.14＝(336－240)×3.14＝96×3.14＝301.44(立方cm)、表面積の差は240×3.14－144×3.14＝(240－144)×3.14＝96×3.14＝301.44(平方cm)と求まります。

　図のかき方が身に付けば得点源にもなります。頑張って練習しましょう。

【第4位　道順：平面での道順の求め方で、角の数の意味を理解できていますか？】

　平面での道順の数え方がわかると、それを利用して立体での道順も考えることができます。次の問題を使って練習してみましょう。　

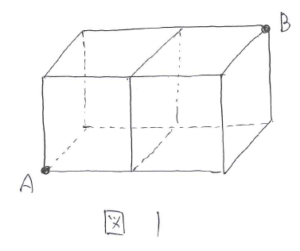
　立方体の辺を1辺ずつ移動していくように考えます。

1回目の移動後は図2のようになります。

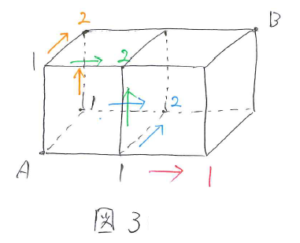2回目の移動後は図3のようになります。

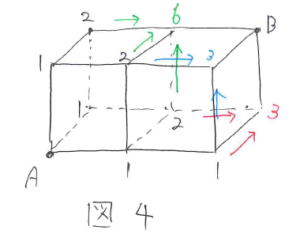3回目の移動後は図4のようになります。

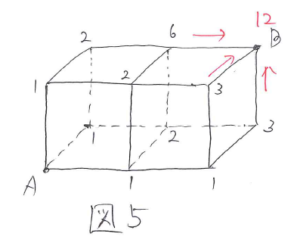4回目の移動後にBにつくので(図5)、答えは12通りと求まります。

　道順の問題では、平面のときも立体のときも1辺ずつ移動していくように考えます。道を戻ったり、数え漏らしたりしないように注意して問題を解きましょう。

【第3位　素因数分解の応用：式を丸暗記するだけでなく、式の意味までしっかり理解を！】

という問題を考えてみましょう。
　例えば、3×10＝30とか320×10＝3200のようにある整数を10倍するとその整数の末尾に0が1つ増えます。このことから、10をかけた回数がわかれば答えが求まることがわかります。ここで注意しなければいけないのは、10＝2×5なので素因数分解をして2と5が1組あれば10が作れるということです。実際に1×2×3×4×5＝120となり「10」をかけてなくても「2と5を1組」かけていれば末尾に0が増えていることが確認できますね。
　あとは素因数分解したときの「2の個数」と「5の個数」を調べます。「2」は偶数に必ず入っているので、少ない方の「5の個数」を調べます。100÷5＝20、100÷(5×5)＝4となりAは一の位から0が20＋4＝24(個)連続して並ぶことがわかります。
　次にAを8で割り続けることを考えます。これも先程と同じく「8」で割らなくても、8＝2×2×2なので「2で3回」割れれば8で1回割ったことになります。
　Aを素因数分解したときの2の個数を調べると、100÷2＝50、100÷(2×2)＝25、100÷(2×2×2)＝12…4、100÷(2×2×2×2)＝6…4、100÷(2×2×2×2×2)＝3…4、100÷(2×2×2×2×2×2)＝1…36となり、2の個数は50＋25＋12＋6＋3＋1＝97(個)とわかります。97÷3＝32…1なので「2×2×2」が32組作れることがわかります。したがって8で「割り切れる」回数は32回となりますが、今回は「割り切れなくなる」のは何回目かということなので、32＋1＝33(回目)と求まります。
　このように素数ではない数で割り続けるときは、素数で割り続けるときと比べて少し考え方が異なります。どちらも重要な考え方ですので整理して考えて間違えないようにしましょう。

【第2位　塗り分け：使う色の数による場合分けは正しくできていますか？】

　塗り分けの問題では、隣り合った場所に同じ色は塗れません。このことに注意しながら考えていきます。慎重に場合分けをしていきましょう。

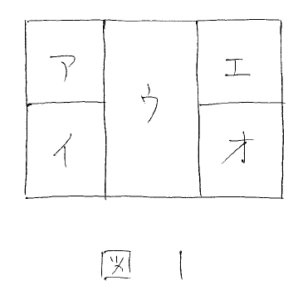
　(1) 5色のときは、ア、イ、ウ、エ、オの5つの場所に塗るので、5×4×3×2×1＝120(通り) と求まります。
　(2) 4色のときは、アとエに同じ色を塗ったとすると、ア(エ)、イ、ウ、オの4つの場所に塗るので 5×4×3×2＝120(通り)となります。また、同じ色が塗れるのは、アとエ、アとオ、イとエ、イとオの4通りあるので、全部で120×4＝480(通り)と求まります。
　(3) 3色のときは、ア(エ)、イ(オ)、ウの3つの場所に塗ると 5×4×3＝60(通り)となります。また、ア(オ)、イ(エ)、ウにも同じように塗れるので 60×2＝120(通り)と求まります。
　以上より、120＋480＋120＝720(通り)と求まります。
　自分で場合分けができるように、いろいろな問題で練習してみましょう。

【第1位　場所を選ぶ：樹形図を使わず計算で解く方法を理解できていますか？】

　予習シリーズ5年上第13回で組み合わせの公式を学習しました。ところがこの公式は「異なるN個のものから2個または3個を選ぶ」というもので、「同じもの」がある場合にはそのままでは使えません。そこで考え方を工夫する必要があります。次の問題を使って考えてみましょう。

　この問題のポイントは、1列に並べるので「前から何番目の玉」という考え方ができる点です。全部で玉が9個あるので前から1番目の玉、2番目の玉、……9番目の玉と区別できるようになります。これを利用して玉の場所を考えていきます。
　まず、個数の少ない黒玉から場所を考えます。玉を並べる場所が9カ所あり、そのうち2カ所を選んで黒玉を並べますので、9×8÷(2×1)＝36(通り)です。次に、白玉の場所を考えます。残った7カ所の場所から、3カ所を選び白玉を並べます。したがって、7×6×5÷(3×2×1)＝35(通り)
となります。赤玉は自動的に決まりますので全部で36×35＝1260(通り)と求まります。
　これらの問題を樹形図で考えることもできますが、かなり大変な作業になります。この考え方は応用できる範囲が広いので繰り返し練習して身につけておきたいですね。

【番外編　第6回から第9回の復習：食塩水や売買損益など割合の問題は徹底復習を！】

　点数にして約３割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第6回　円・おうぎ形の公式、複合図形の面積・まわりの長さ
　・第7回　食塩水の基本操作(食塩水を加える、水を加える、食塩を加える、蒸発させる)
　・第8回　仕入れ値(原価)と定価と売り値と利益の関係
　・第9回　差集め算の基本、取り違えの問題

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。