メールマガジン宝箱 Mail magazine

　6年の前期も押し迫ったこの時期になると、基本パターンで解ける問題は減り、問題内容を正確に理解したうえで、これまでに習った解法を組み合わせて解く力が求められる問題が多く出されるようになります。
　そこで、対策ポイントをプロ家庭教師の視点から3つのポイントにまとめました。ぜひ偏差値アップ、クラスアップを実現してください。応援しています！　　
　さらに、このランキングは明後日6/19（金）公開の予想問題と連動していますので、予想問題も合わせてご利用ください！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：場合の数の金額を決める問題で表を有効に使えていますか？】

　場合の数の問題の中で、指定された硬貨を使ってある金額を設定するタイプの問題があります。計算で解き進めるよりも、表を使って解く方が、速く確実に解けることが多くありますので、表のまとめ方について整理しておきましょう。次の問題を例にします。

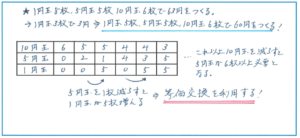
　このタイプの問題でまず気をつけるのは、「使わない硬貨があってよいかどうか」です。その条件によって解き方が全く変わってきますので注意しましょう。
　さらにこの問題では、合計金額の1の位に注目することも大事です。63円の1の位である3円をつくることができるのは1円玉を3枚使うのみです。そこで、まずは1円玉3枚を使って、残り60円を1円玉(8－3＝)5枚、5円玉5枚、10円玉6枚を使って作るといった問題になります。
　ここからは、もれなく、速く組合せを考える方法を考えてみましょう。60円を作る際に、1円玉を5枚使って、次に5円玉を5枚…と小さな金額の硬貨を中心に考えるよりも、大きな金額の硬貨を中心に考える方がスムーズに進められます。まずはすべてを10円玉で作る、10円玉6枚のみのパターン。これは1通りですね。次に10円玉の枚数を1枚減らして、10円玉を5枚とすると残り10円なので、これを5円玉2枚とする。そこからは、10円玉5枚は固定して、10円を5円玉1枚と1円玉5枚で作ると60円になります。次に5円玉を1枚減らすと、10円玉5枚、5円玉0枚で残り10円となりますが、1円玉は5枚しかありませんので、このかたちでは60円は作れなくなります。
　そこからは、10円玉を4枚にして、5円玉を4枚として、同じように大きな金額の硬貨の枚数を減らして表をうめていきますが、ここでぜひ気づいて頂きたいことがあります。等価交換の考え方です。10円と5円の金額の比は10：5＝1：2ですので、同じ金額を作る際に10円玉を1枚減らすと、5円玉は1×2＝2（枚）増えることになります。同じく5円玉を1枚減らした場合、金額を変えないためには1円玉を1×5＝5（枚）増やせばよいのです。このルールにそって進めれば、表の作成が断然早くなります。
　結果として表から6通りと答えが導き出せますが、あてはまるケースをただ書き出すよりも、表を使ってルールにそって進める方が、ミスも防ぐことができます。ぜひ表を使った解き方を実践してみてください。

【直前チェックポイント２：ブーメラン型の面積比の求め方は覚えられていますか？】

　今回のテストでは平面図形の面積比の問題が出題される可能性が高くあります。高さが同じ三角形の面積比が底面の長さの比になることなどの基本パターンはしっかりおさえておくとして、次のようなブーメラン型の図形の面積比も、ガッチリ固めておきましょう。

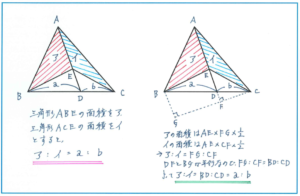
　この解法パターンは例えば速さや食塩水の公式のように、覚えていなければ問題を解くことさえできないものではありません。上記のように補助線を引いて相似の考え方を使って自分で面積比を求めることができます。ただ、そのプロセスを経るよりも覚えてしまっている方が断然早く解き進めることができますね。それでも解法パターンを丸暗記するだけでなく、プロセスまで覚えておけば、より記憶が深く定着しますので、補助線の引き方にも注意を払っておくようにしましょう。
　平面図形で相似と共に出題頻度が高いのが面積比の問題です。このブーメラン型の図形のように、解法を覚えておくだけでより早く正確に答えに行き着ける図形のパターンを多く覚えておくことは、問題を見た瞬間に正解へのプロセスが頭の中に浮かび、その問題を正解できるだけでなく、解法を正しく使いこなしたことへの大きな自信が生まれ、テストを解き進める勢いをも生み出します。ぜひ図形の解法パターンをひとつひとつ自分の中に積み重ねていってください。

【直前チェックポイント３：相似の関係が見つからない場合は線を延長しましょう！】

　相似では、ピラミッド型などの典型的な相似の図形が問題の図の中に明らかに見て取れるような基本問題から難度が上がった問題が出される頻度が上がりますが、皆さんがこれまで習ってきた解法はしっかり使えますので、心配せずに、問題を解き重ねて、新たなパターンを身につけていきましょう！
　問題の図に相似の関係が見つからない場合には、平行線を図形の内部にひいて、図形を切り取るかたちで相似の関係を作り出す方法と、既存の線を延長して図形を広げるかたちで相似の関係を作り出す方法があります。ここでは視点の切り替えが必要となる後者について例を挙げて説明していきましょう。
　次のような問題です。

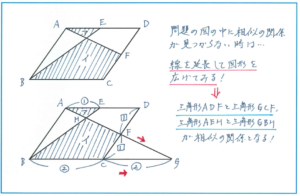
　ここではＡＦとＢＣを延長させて点Ｇを作り、三角形ＡＤＦと三角形ＧＣＦという相似（ここでは合同になっています）の関係、さらに三角形ＡＥＨと三角形ＢＧＨの相似の関係を作り出すことがポイントですが、もともとの図をよく見ると、ＡＤとＢＣが平行であることから、三角形ＡＥＨと相似の関係にある三角形がある可能性が見えます。「ＢＣがもう少し長ければ三角形ＡＥＨと相似の関係にある三角形が見つけられる」といったイメージを持つことが大事なのです。あとはその三角形を作るために、もとの図形の外部にまで目を行き届かせる、視点を広げる意識を練習で培っていけば、相似の問題の得点力が大幅にアップします！
　この問題では、Ｆが辺ＣＤの真ん中の点なのでＤＦ＝ＦＣより、ＡＤ＝ＣＧとなり、ＡＥ：ＡＤ＝1：2、ＡＥ：ＢＧ＝1：4になります。ここでＡＧに注目すると、ＡＦ：ＧＦ＝1：1、ＡＨ：ＧＨ＝1：4より、ＡＧの長さを10とすることで、ＡＨ：ＨＦ：ＦＧ＝2：3：5を導き出せます。ここから、三角形ＡＥＨの面積を1とすると、三角形ＡＤＦの面積は2×5/2＝5、三角形ＧＣＦの面積も5となります。三角形ＢＧＨの面積は4×4＝16となりますので、四角形ＢＣＦＨの面積は16－5＝11となり、ア：イ＝1：11と求められるのです。
　視点を広げるうえでも、相似の基本的なパターをおさえられていれば、イメージを確かに抱くことができます。まずは基本パターンを今一度確認して、今回のようなタイプの問題の演習を重ねましょう！

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。