メールマガジン宝箱 Mail magazine

　組分けテストは範囲がなく、さらに夏休み前のこの時期になると、基本的な解法を使うだけでなく、これまで習った解法を組み合わせて解く応用力が求められる問題が多く出題されますので、ポイントをいかに絞って復習するかが重要になります。
　そこで、対策ポイントを、プロ家庭教師の視点から第5位から第1位までのランキングのかたちにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
さらに、このランキングは明日公開の予想問題と連動していますので、予想問題も併せてご活用ください！
予想問題はこちらのページで1週間限定で無料公開します！

【第5位　場合の数：金額の場合の数を計算で求める方法を覚えられていますか？】

　場合の数の中で、3種類の硬貨を何枚かずつ組み合わせてできる合計金額が何通りあるかを求める問題があります。例えば次のような問題です。

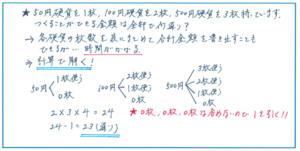
　このような硬貨の組み合わせの問題では、表を用いて合計金額を書き出す方法があります。その場合は、単価の高い（この問題であれば500円硬貨）を使う枚数から場合分けする方法があります。順番に組み合わせを書き出すことで、場合の数がもれてしまうミスを防ぐことができますので、表を使った解法は覚えておきましょう。
　ただ、この問題では表に書き出さす組み合わせの数が多く、時間がかかってしまうことが予想されます。そこで、計算を使う解法も身につけておきましょう。
　50円硬貨を例にとると、1枚使う、1枚も使わない、の2通りの支払い方法が挙がります。100円硬貨は3通り、500円硬貨で4通りとなり、積の法則で2×3×4＝24（通り）という計算結果になります。このタイプの問題はここからが細心の注意が必要になります。3つの硬貨すべてを1枚も使わないとなると合計金額が0円になり、問題の答えには該当しなくなります。よって24－1＝23（通り）が正解になるのです。計算で解き進める場合は、時間が短縮できる大きなメリットがありますが、最後の詰めまで気をつけておかなければ失点につながりますので、十分に注意しましょう。

【第4位　平面図形：15度、150度が出てきた時は二等辺三角形に注目しましょう！】

　平面図形の問題で、30度・60度・90度の直角三角形の、60度をはさむ辺の長さの比が2：1になることを利用するパターンには皆さんも慣れてきたと思います。このパターンをさらに広げて二等辺三角形のかたちで活用する方法を覚えておくと、面積を求める問題での得点力が大きくアップします！
　例えば次のような問題です。

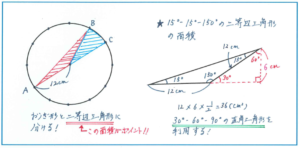
　まずは斜線部の図形がおうぎ形ではないことに注意しましょう。おうぎ形は円の中心を必ず通りまが、上の図の斜線部は円の中心を通っていません。見た目が似ているからといって、おうぎ形と判断しないようにしてください。
　ここでは円の中心と点Ｂを結ぶ線で、図形をおうぎ形と三角形に分けます。おうぎ形の中心角は360÷12＝30（度）となるので、面積は容易に求められます。
　ポイントは頂角が150度の二等辺三角形の面積の求め方です。150度の外角が30度であることから、右の図のように、三角形の外側に30度・60度・90度の直角三角形をつくることができます。そこで二等辺三角形の高さが12÷2＝6（cm）となることから、面積を12×6÷2＝36（平方cm）と求められます。結果として、斜線部全体の面積は、12×12×3.14×30/360＋36＝37.68＋36＝73.68（平方cm）と求められます。
　二等辺三角形で頂角が150度、または30度の際には、30度・60度・90度の直角三角形を見つけられるように三角形の見方を鍛えていきましょう。

【第3位　水そうの問題：水そうの断面図を使った解き方を覚えられていますか？】

　水そうにおもりを沈めた際の深さの変化を求める問題では、断面図で変化の様子を把握したうえで、比を用いて解く方法をしっかり確認しておきましょう。
　例えば次のような問題です。

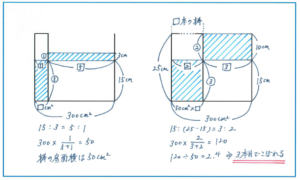
　まずは棒を1本入れたときの水の深さの変化の様子を断面図にして、棒の底面積を求めます。断面図は上の左のようになります。斜線の入った部分が同じ面積になることから、面積図の考え方で比を利用しましょう。棒の底面積は300平方cmを5：1に分けた1にあたりますから、300×1/(5＋1)＝50より50平方cmと求められます。
　ここから棒を続けて入れるという内容に進みますが、断面図で解く方針は変わりません。「水がこぼれる」とありますが、水が容器いっぱいになる状態を考えれば、そこから1本でも多く入れれば水はこぼれますので、右のような断面図で考えてみましょう。
　やはり面積図の考え方で、300平方cmを3：2に分けた2の部分の面積が、容器がいっぱいになった際の棒の底面積の和です。300×2/(3＋2)＝120（平方cm）より、120÷50＝2.4という計算結果になります。棒を2.4本入れることはありませんので、答えは3本目となります。この最後の計算結果からの答えの求め方に注意しましょう。
　水の深さの変化の問題は、変化の様子をイメージするのが難しいですが、断面図で考えれば、面積図の解法を使うことができます。一連の流れを確認しておきましょう。

【第2位　約数の個数：素因数分解を使う前に約数の並び方に注意しましょう！】

　整数の約数に関する問題では、約数の個数が大きなヒントになります。個数が奇数の場合に、もとの整数が平方数になることはすでに覚えられていると思いますが、偶数の場合でも個数が考え方のベースになります。その場合は、約数の並び方に注目しましょう。
　例えば次のような問題です。

　約数の個数が偶数になる場合には、約数を並べた際の対象の位置にある約数どうしをかけ合わせると整数Ａになります。この問題では約数が12個ですので、1番目と12番目、2番目と11番目、3番目と10番目…と対称の位置にある約数をかけ合わせると整数Ａになります。
　ここからは素因数分解の考え方を使っていきます。約数としてわかっている8と18をそれぞれ素因数分解すると、8＝2×2×2、18＝2×3×3となるので、整数Ａの約数に2の倍数と3の倍数が含まれることがわかります。そこでさらにわかった約数を書き出していくと、下の図のようになります。7番目の約数が9とわかりますので、整数は8×9＝72と求めることができるのです。
　約数の問題は問題文からわかるヒントが必ずしも多くありませんが、約数の並び方や素因数分解を使うといったポイントを使えれば、正解に行き着くことができます。

【第1位　平面図形：三角形の面積比の問題で使う3つのパターンはすぐに浮かびますか？】

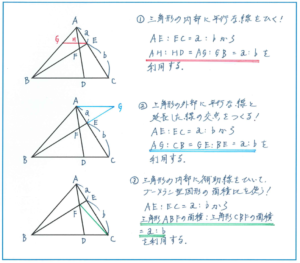
　平面図形の問題では相似や面積比を使って解く問題が出題される可能性が高くあります。平行四辺形や台形の問題ではすでに平行な辺の関係があるので、解法のきっかけがつかみやすいですが、三角形になると難度が上がります。三角形で長さの比が与えられ、そこから面積比を求める場合に、三角形の見方に3つのポイントがあります。
　平行線を自分でつくるためには、三角形の内部に平行線を引く（下のマル1）、三角形の外部に延長線を引いて平行な線をつくる（下のマル2）があります。マル1の場合は線のひき方がイメージしやすいですが、マル2の延長線を利用するケースは、どの線を延長させればよいのかがすぐには浮かばないでしょう。このケースでは、相似の典型的なパターンをもとに、ここに相似の図形があれば解き進められるという方針を固めることでイメージがしやすくなります。
　特に気をつけておきたいのがマル3のブーメラン型の図形での面積比を使う解法です。このかたちでの長さの比と面積比の関係を使いこなせれば、正解できる面積比の問題が圧倒的に多くなります！　

　解法を多く身につけて、問題内容に合わせた対応ができるようにして、自信を持ってテストに臨みましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。