メールマガジン宝箱 Mail magazine

　5年生の皆さん、夏期講習ではどのような問題を解いたか思い出してみましょう。どんな問題を解いて、どのような間違いをしたかをふり返ることはとても大切です。主に、平面図形、数の性質、割合に関する問題を中心に学習したことと思います。ふり返りをしっかりとして、夏期講習の頑張りをテストでの得点に結び付けたいところです。
　そこで、9/5（土）の実力判定テストの対策ポイントをプロ家庭教師の視点から5つのポイントにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明日8/28（金）公開の予想問題と連動していますので、予想問題も合わせてご利用ください！
予想問題はこちらのページで無料公開します！

【直前チェックポイント第5位：複数の割合が出てくる売買損益の問題を線分図で整理できていますか？】

　100円の4割と300円の4割では、もちろん答えが違いますよね。同じ4割でも、どうして答えが違ってくるかというと、一方は基準が「100円」で、もう一方は基準が「300 円」だからです（基準を「もとにする量」とも呼びます）。
　同じように、仕入れ値の4割と定価の4割でも答えが違ってきます。同じ4割でも、一方は基準が「仕入れ値」で、もう一方は基準が「定価」だからです。基準が異なる割合が出てきた問題では、計算によってどちらか一方の基準に合わせておくと、スピーディに解答することができます。実際に問題を解いて理解していきましょう。

　この問題のポイントは、売値について、定価ではなく仕入れ値を基準にするとどれくらいの割合にあたるのか計算することです。
　まず、「仕入れ値の5割を見込んで定価をつけた」を式で表すと、定価＝仕入れ値×1.5 です。この式の大切な意味は、「定価」という文字は「仕入れ値×1.5」に置き換えることができる、ということです。式は単に計算の結果を表すだけではなく、言葉を別の言葉に置き換える道具にもなるということは覚えておいてください。
　次に、2日目の売値を「定価の2割引きで売る」とは、「定価の8割にする」すなわち「定価の0.8倍にする」ということです。式で表すと、定価×(1－0.2)＝定価×0.8です。
　では、この式の「定価」を「仕入れ値×1.5」で置き換えましょう。定価×0.8＝仕入れ値×1.5×0.8です。つまり、定価×0.8＝仕入れ値×1.2です。
　すなわち、2日目の売値＝仕入れ値×1.2だということがわかりました。もういちど計算式を繰り返します。
　定価＝仕入れ値×1.5
　2日目の売値＝定価×0.8
＝仕入れ値×1.5×0.8
＝仕入れ値×1.2

　基準を仕入れ値に合わせたので、仕入れ値を①とおいて線分図で表してみましょう。とてもすっきりと書くことができます。
　図1のようになります。

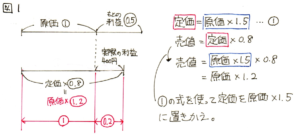
　ここで、実際の利益400円の部分の割合は1.2－1＝0.2にあたります。よって①＝400÷0.2＝2000円です。①が仕入れ値そのものですから、答えは2000円となります。

【直前チェックポイント第4位　複数の割合が出てくる相当算の問題で、図を使わずに解く方法を使いこなせていますか？】

　次に、相当算について考えてみましょう。相当算にはいくつかの解き方がありますが、問題によっては特定の解き方をすると素早く解くことができ、時間と労力の節約にもなります。

　今回は基準を「全体」に合わせる方法を身に付けましょう。

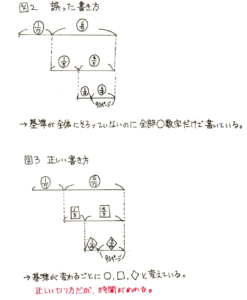
　この問題のポイントは、1日目の基準は「全体」ですが、2日目は基準が「1日目の残り」、3日目の基準が「2日目の残り」ということです。図2のように、基準が変わっていることに気づかないまま線分図を書くと、ミスにつながります。
　図3のように、きちんと記号を分けて書くのが正しい線分図の書き方です。これはこれで問題はありませんが、今回は、もっと時間を節約できて脳に負担がかからないやり方があります。計算で求める方法です。
　例えば、全体の半分の半分の半分っていくつになりますか？
　1/2 ×1/2 ×1/2 ＝1/8 ですから、全体の1/8 になります。
　同じように、3日目の残りというのは、残りの残りの残りということですから、
　6/7×4/5×3/4＝18/35ということになります。
　つまり、3日目の残りは、全体の18/35にあたるということです。
　ところで、6/7、4/5 、3/4って何の意味だかわかりますか？
　各日にちの残りの割合のことです。すなわち、1日目の残りは1－1/7＝6/7、2日目の残りは1－1/5＝4/5、3日目の残りは1－1/4＝3/4と表されるのです。
　話を戻して、18/35が90ページにあたり、求めたい全体のページ数が1にあたるので、
　　90÷18/35＝175ページです。
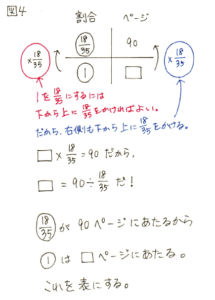
　ところで、試験本番になったりするとあわててしまって、この90÷18/35の式がパッと思いつかず、「えーと、×だっけ、÷だっけ？」なんてあわててしまったこと、ありませんか？そういうときは、図4のような十字の表を書いてみると、かんたんに正しい式を導くことができますよ。

【直前チェックポイント第3位　売買損益で品物が多数出てくる問題を、面積図を書いて解く方法があります！】

　売買損益の問題には、品物が1個しか出てこない問題と、品物が多数でてくる問題とがあります。品物が1個の場合は線分図で、品物が多数の場合は、線分図ではなく面積図を書いたほうがよいです。

　まず、面積図を書く前に、(問1)でやったように、基準を仕入れ値に合わせておきましょう。「4割の利益を見込む」とは、定価を「仕入れ値の4割増し」すなわち「仕入れ値の1.4倍」にするということです。
　また、(問１)でやったように「定価の2割引き」とは売値を「定価の8割にする」ということでした。これを仕入れ値を基準にして計算し直します。
　　定価＝仕入れ値×1.4 売値＝定価×0.8
　　売値＝仕入れ値×1.4×0.8＝仕入れ値×1.12
　これで面積図を書く準備が整いました。図5を見ながら読み進めてください。

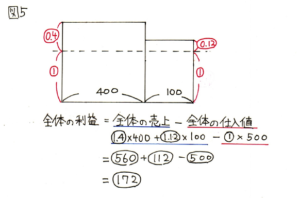
　面積図の書き方ですが、縦を仕入れ値や売値などの値段、横を個数として面積図を書いていきます。基準を仕入れ値に揃えたので、仕入れ値を①とおき、その他の割合を書き込んでいきます。また、売買損益の特徴として、仕入れ値が大切なことが多いので、仕入れ値の部分に横線を入れておくとよいです。
　ここで、重要な式の登場です。全体の利益＝全体の売上－全体の仕入れ値という関係を使って解いていくと、スムーズに解き進められます。ぜひこの関係式は試験のときに使えないか試してみましょう。図全体の利益が172になりました。これを全体の仕入れ値で割れば、答えが出てきます。
　答えは百分率で出すので、計算のなかで100倍するのを忘れずに。
　　172÷500×100＝34.4より、
　答えは、34.4％です。

【直前チェックポイント第2位　図形の転がりでおちいりやすいミスを把握しましょう！】

　長方形の内側にそって転がるとき、その円が通る面積を求める問題があります（ここで内側とは、長方形の90度の部分をいいます）。

　このときにおちいりやすいミスを、図6に示します。

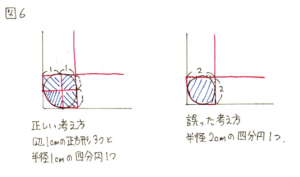
　図6の右側のように、90度で曲がる際の範囲を、単純に半径2cmの四分円としないようにしましょう。正確には、左側のように、1辺1cmの正方形3つと、半径1cmの四分円1つに区切られます。

【直前チェックポイント第１位　円やおうぎ形を含む図形問題は、半径に補助線を引いて二等辺三角形をつくろう。記号を利用して外角の定理を使いこなそう！】

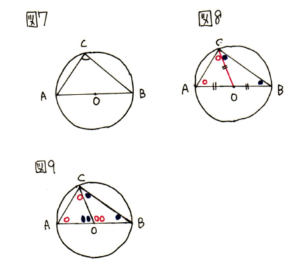
　半径は、中心から出る線のことですからOから補助線を引けないか考えてみましょう。図8のように、OCに補助線が引けます。
　半径に補助線を引く意味は、半径はどこも同じ長さなので、二等辺三角形や正三角形を作ることができ、しかもそれが重要な足がかりになるということです。
　二等辺三角形が2つ出現しました。三角形OACと三角形OBCは二等辺三角形です。
二等辺三角形をつくったら同じ角度の部分に記号を入れましょう。こうすることで、角度の関係がずっとわかりやすくなります。
　さらに、ここで外角の定理を思い出しましょう。「三角形の2つの角度の和は、残りの外角に等しい」というものでした。これを利用すると、図9のように、角COBは○○、角COAは●●と表せます。
○○●●＝180ですから、○●＝180÷2＝90度です。よって角Cの大きさは90度です。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。