メールマガジン宝箱 Mail magazine

　塾の授業で比の演習が進み、テスト問題でも比を利用して解く問題が増えてきます。比を使いこなすためにも、問題内容を正確に理解する解法を身につけておきたいところです。
　そこで、11/7（土）の実力判定テストの対策ポイントをプロ家庭教師の視点から5つのポイントにまとめました。ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このランキングは明後日10/30（金）公開の予想問題と連動していますので、予想問題も合わせてご利用ください！
予想問題はこちらのページで無料公開します！

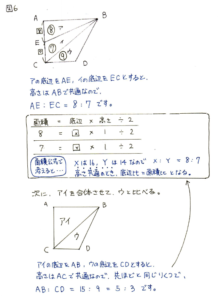
【直前チェックポイント第5位：やりとり算を1本の線分図で整理できていますか？】

　中学受験の算数では、和や差に着目することが大切な発想法の1つです。これは比のときも同様です。
　たとえば、3:4であれば、比の和は③＋④＝⑦です。比の差は④－③＝①と表すことができます。
　このように、3:4の③や④に着目するだけではなく、和の⑦や差の①に着目しないと解けない問題があります。

　この問題には○：□といった表現は出てこず、○倍という割合しか出てきません。こういう場合、A＝B×2.5、B＝C×2、などと式を作って解いてもいいのですが、割合が出てきたら、比を積極的に活用するようにすると解きやすくなります。
A:B＝2:5、B:C＝2:1なので、A:B:C＝4:10:5です。
これをもとに線分図を書きます。④や⑩や⑤それぞれに着目するのではなく、比の和である⑲に着目することです。

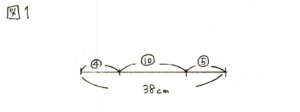
④＋⑩＋⑤＝⑲
⑲＝38cm
①＝2cm
④＝8cm
答えは8cmです。

　もうひとつ、比の和に着目する問題に挑戦しましょう。次のような問題を「やりとり算」といい、ぜひこの時期にマスターしておきたい問題です。ポイントは、2人の間でお金をやりとりしているだけなので、やり取りしている前後で2人の金額の和は変わらないということです。

　やりとり算では、線分図は1本線になります。やりとり前後の比を○と□で区別します。

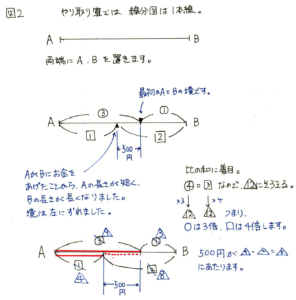
500÷5＝100
100×9=900円
答えは900円です。

【直前チェックポイント第4位：同じ量が増減するときは線分図の左端にそろえましょう！】

　今度は比の差に着目する問題に挑戦しましょう。

　太郎くんが次郎くんの2.5倍なので、太郎:次郎＝5:2として、線分図を書いていきましょう。
　同じ量が増えたり減ったりした問題では、増減した分を左側にそろえて線分図を書くことがポイントです。

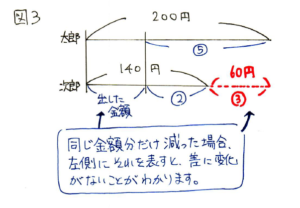
金額を出し合った前後で差に変化はありません。したがって、③＝60円が決まります。
①＝20円
②＝40円
はじめ次郎くんは140円持っていて、現在40円になりましたから、出したのは100円です。
太郎君も同じ金額である100円出しましたから、お菓子の値段は200円と求められます。

【直前チェックポイント第3位：平均の問題では面積図を書いて、逆比を活用しましょう！】

　ちょっとひねった平均の問題では、式だけを使って解こうとすると困ってしまうことが多いです。そういう場合は、ぜひ面積図を書いてください。その際に着目するべきいくつかのポイントがあります。見逃さないようにしましょう。
　平均の問題で面積図を書くときは、たてを点数、よこを人数とするといいでしょう。今回は人数はわからないですが、比はわかっています。
　積が一定の場合、かけるものの比とかけられるものの比は逆比になることは逆比のところで学習しました。平均の問題で面積図を使うときは、この性質を使いますので、しっかり活用しましょう。

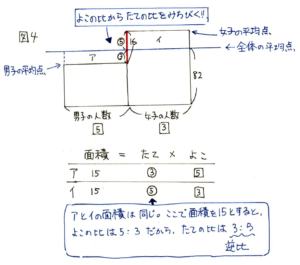
たての比は、ア:イ＝3:5だということがわかりました。
ここで比の和に着目すると、⑧＝16点です。ここまでくればあともう一息です。
①＝2
⑤＝10
女子の平均点は、全体の平均点82点より⑤だけ高いですから、
82＋⑤＝82＋10＝92
答えは92点です。

【直前チェックポイント第2位：辺の長さの比と面積比の関係は、面積公式から導かれます！】

　三角形と平行四辺形を比べる問題です。これが三角形同士であれば簡単に解けるのですが、三角形と四角形を比べられると正答率が落ちます。各辺の比を面積公式と結びつけて考えることが大切です。
　この分野は「解けるけれど、りくつがわからない」ということが多いので、しっかりと理解を重ねましょう。
　まず、底辺の比を出してしまいましょう。SがRの1.2倍ということですから、Sの底辺:Rの底辺＝6:5です。
　三角形の面積は、底辺×高さ÷2ですから、これに比をあてはめますと、
　6×4÷2＝12
　同様に、平行四辺形の面積は底辺×高さですから、これに比をあてはめますと、
　5×7＝35
　よって、S:R＝12:35より、答えは12:35です。

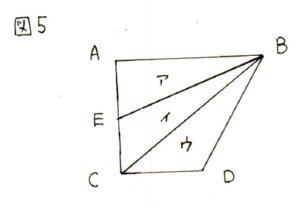
　この問題も、高さが同じとき、底辺の比＝面積比だということは理解できていると思いますが、今いちど、面積公式にあてはめてその理由を理解しておきましょう。

【直前チェックポイント第1位：食塩水の問題も平均算と同じように面積図で解決できます！】

　食塩水の問題は、比ととても相性のよい問題です。ちょっとひねった問題では、式と計算だけで解決しようとしても苦戦するかもしれません。複雑な問題は、平均の問題と同じような面積図を書いて考えるようにしましょう。
　食塩の重さ＝濃度×食塩水全体の重さ
です。長方形の面積はたてとよこの積ですから、面積は食塩の重さを表します。
したがって、たての長さを濃度、よこの長さが食塩水全体の重さ、面積が食塩の重さを表します。

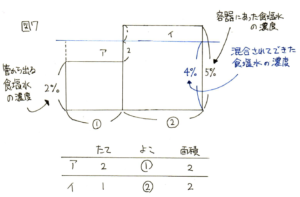
図より、①が100÷2＝50（g）になりますので、
50÷10＝5より、
答えは5秒間となります。

アとイの面積が同じですから、たての長さの比はよこの長さの逆比になることをしっかりおさえておきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。