メールマガジン宝箱 Mail magazine

　今回の組分けテストは5年生、4年生ともに線分図をかいて問題内容を整理することが偏差値アップのポイントです！5年生は旅人算、4年生は分配算で線分図を活用できれば、得点差を大きくつけられます。そのためにも、問題に合わせた図のかき方を、チェックしておきたいところです。
　そこで、ぜひ気をつけて頂きたいポイントを、プロ家庭教師の視点から5年生は第5位から第1位まで、4年生は第3位から第1位までのランキングにまとめました。メルマガを読んで、ぜひ偏差値アップ、クラスアップを実現してください！応援しています！
　さらに、このメルマガの5年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する対策ポイントと予想問題を合わせれば、偏差値アップのための万全の準備が整います！頑張りましょう！
予想問題はこちらのページで無料公開します！

5年 第7回組分けテスト

【第5回　速さのつるかめ算：速さの比の値を使って道のりを表せていますか？】

　「速さのつるかめ算」の考え方をもとに、速さの比を使って解いていく問題です。「速さのつるかめ算」は予習シリーズ5年上第16回で学習した内容です。忘れている場合は、そちらの確認から始めましょう。

という問題を考えてみましょう。
　まず速さの比を求めます。「道のりが一定のとき、速さの比と時間の比は逆比」という関係があるので、時間の比が 歩：走＝35：10＝7：2 ですから、速さの比は 歩：走＝2：7となります。
　次に家から駅までの道のりを速さの比を使って決めます。歩く速さをマル2とすると、道のりは マル2×35＝マル70 と決めることができます。
　最後につるかめ算を使って走った時間を求めます。走る速さをマル7とすると（マル70－マル2×20）÷(マル7－マル2)＝6(分間)と求まります。
　比を使った「速さのつるかめ算」の典型的な問題でした。組分けテストに限らず、入試問題でもよく出題されていますのでしっかり練習して確実に身につけましょう。

【第4位　直角三角形の相似：補助線を引いて相似な図形を作れていますか？】

　直角三角形はすでに直角があるので、もう1つの角度が等しくなれば「2組の角度がそれぞれ等しい」という三角形の相似条件が成り立ちます。図形のなかに直角三角形があるときは注意が必要です。

という問題を考えてみましょう。

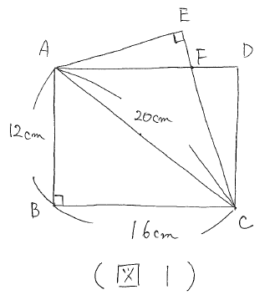
  折り返した図形は合同になっているので、角ACB＝角ACEがわかります。また、ADとBCは平行なので錯角が等しいことから、角ACB＝角CAFがわかります。以上の事から、三角形ACFは二等辺三角形だとわかります。
　次にFからACに引いた垂線の足をHとすると、三角形ACFが二等辺三角形なのでHはACの中点になります。(図2)

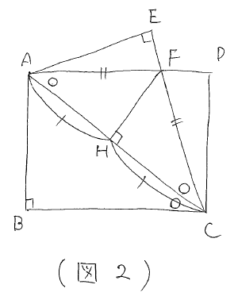
　ここで、三角形ABCと三角形FHCは2組の角がそれぞれ等しいことから相似になります。したがって辺の比が等しくなります。(図3)

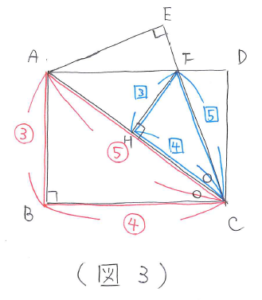
　(図3)からシカク4＝20÷2＝10(cm)、シカク1＝5/2(cm)、シカク3＝15/2(cm)となり、三角形ACFの面積は、20×15/2÷2＝75(平方cm)と求まります。
　一見すると相似はありませんが、この問題のように自分で補助線を引いて相似を作ることもあります。直角三角形で直角以外に等しい角度があるときは、相似が使えることを覚えておきましょう。

【第3位　数表：求める数に近い平方数がすぐに浮かびますか？】

　数表の問題では、三角数や平方数に注目するときまりがわかることが多いです。どちらもよく出題されるので、すぐに見つけられるように練習しましょう。

という問題を考えてみましょう。

　表を見ると、1、4、9、16、…と平方数があります。奇数番目の組は右上から左下へ、偶数番目の組は左下から右上へ、順番に数字が並んでいます。(図2)

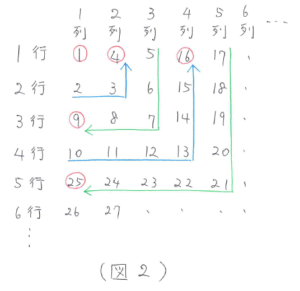
　ここで、2020に一番近い平方数を探します。40×40＝1600、50×50＝2500なので、この間だとわかります。さらに調べると、45×45＝2025が一番近いとわかります。
　45は奇数なので、2025は45行目の1列目にあります。よって、2020は45行目の6列目と求まります。
　規則性の問題では、見当をつけて調べたり範囲を絞って書き出したりすることが必要になることがあります。最後まで粘り強く考えましょう。

【第2位　図形の折り返し：図形の中から解答に必要な相似を見つけ出せていますか？】

　　折り返しの問題の典型題です。繰り返し練習して考え方を身につけましょう。

という問題を考えてみましょう。

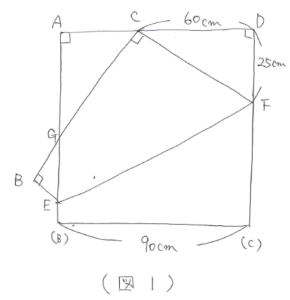
　三角形FDCと三角形CAGと三角形EBGは相似(※)になります。
　三角形FDCの辺の比は、FD：DC：CF＝25：60：(90－25)＝5：12：13となっているので、CA：AG：GC＝EB：BG：GE＝5：12：13(図2)となります。

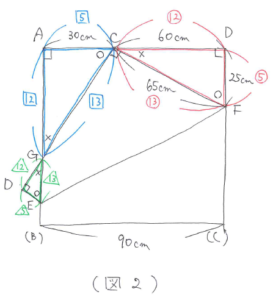
　これを利用して長さを求めると、GC＝(90－60)×13/5＝78(cm)、BG＝90－78＝12(cm)、BE＝12×5/12＝5(cm)となります。したがって、四角形GEFCの面積は(5＋65)×90÷2－5×12÷2＝3120(平方cm)と求まります。
　平面図形の問題では図が不正確な場合も多いです。相似を考えるときは辺や角度に印を付けて対応関係を間違えないようにしましょう。
※ 角DFC＝〇、角DCF＝×とすると、三角形FDCの内角の和から 〇＋×＋90＝180(度)となります。また、一直線は180度なので、角ACG＝180－(90＋×)＝〇 となり角DFC＝角ACGとわかります。三角形CAGの内角の和から角AGC＝180－(90＋〇)＝×、対頂角は等しいので、角BGE＝角AGC＝×となります。以上より2組の角がそれぞれ等しいので、三角形FDCと三角形CAGと三角形EBGは相似になります。

【第1位　往復の旅人算と比：2回目の出会いが道のりの3倍になることがポイントです！】

　予習シリーズ5年上第19回で学習した「往復の旅人算」で比を使った典型的な問題です。旅人算の考え方を忘れていると手も足も出ないので、その場合は予習シリーズ5年上第18回、第19回の復習から始めましょう。
　次の問題を考えてみましょう。

　進行図に状況を整理しながら考えましょう。A地とB地の真ん中をM地点、1回目に出会った場所をC地点として図をかきます。
「時間が一定のとき、道のりの比と速さの比は等しい」のでAC：CB＝7：5 となります。ACの道のりをマル7、CBの道のりをマル5とすると、AB＝マル7＋マル5＝マル12、AM＝マル12÷2＝マル6、MC＝マル7－マル6＝マル1 となり、マル1＝120mとわかります。(図1)

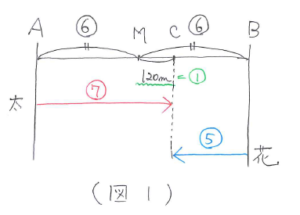
　次に2回目に出会ったときを考えます。2回目に出会った場所をD地点として、もう１つ進行図をかいてみましょう。太郎君はB地を、花子さんはA地を折り返してD地点で出会った図になります。(図2)

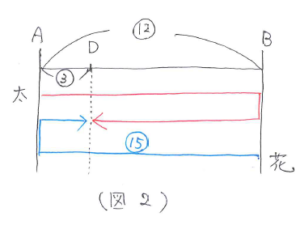
　ここで(図1)と(図2)の進行図を見比べると、(図1)の進行図は太郎君と花子さんの2人でAB間１本分の道のりを移動しているのに対し、(図2)の進行図は太郎君と花子さんの2人でAB間3本分の道のりを移動しています。このことから、3倍の時間がかかっていることがわかります。
　したがって花子さんがB→A→Dと移動した道のりは マル5×3＝マル15 となり、AB＝マル12よりAD＝マル15－マル12＝マル3となります。マル1＝120(m)より、マル3＝360(m)となり、答えは360ｍと求まります。
　往復の旅人算でN回目に出会う問題は数多く出題されているので、練習する機会も多いと思います。それだけに何度も繰り返して完全にマスターできるよう頑張りましょう。

【番外編　第1回から第4回の復習：逆比の解き方を覚えられていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第1回　比の積・比の商、連比
　・第2回　比例式、逆比、倍数算
　・第3回　高さが等しい図形の面積比
　・第4回　相似、縮尺

4年　第7回組分けテスト

【第3位　分数：まだ約分できる分数をそのままにしていませんか？】

　分数では「約分」と「通分」がしっかりとできることが重要です。その分数がまだ約分できるかどうかに気付くためは訓練が必要です。毎日計算などを繰り返して練習しましょう。

　という問題を考えます。
　分母を18にそろえると、1/4は分母が18÷4＝4.5(倍)になっているので、分子は1×4.5＝4.5となります。したがって、4.5/18より大きく15/18より小さい分数だとわかります。
　分子が2の倍数または3の倍数だと約分できてしまうので、4.5より大きく15より小さい2の倍数でも3の倍数でもない数を調べます。その結果 5、7、11、13、となります。
　したがって求める分数の和は、5/18＋7/18＋11/18＋13/18＝2 と求まります。
　分母がわかっているときは分母を、分子がわかっているときは分子をそろえるのがポイントになります。一方がそろってしまえば、もう一方だけを考えれば済むからです。繰り返しになりますが、約分・通分がスムーズにできるようになるまで練習しましょう。

【第2位　方陣算：等差数列の和の公式を正確に覚えられていますか？】

　方陣算のポイントは「重ならないように同じ形に分ける」というところです。簡単な図をかくだけでミスが減らせます。必ずかくようにしましょう。

という問題を考えてみましょう。
　小さい形で練習してみましょう。一番外側の1辺に4個の碁石が並んでいる正六角形をかきます。すると一番外側のひとまわりに並んだ碁石の数が、4×6＝24(個)ではないことに気が付くと思います。

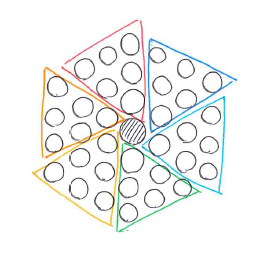
　これは正六角形の頂点にあたる碁石を2回数えてしまっているためです。「重ならないように同じ形に分ける」ように考えると、1辺を4－1＝3(個)とすると上手く分けられます。また全体の個数ですが、今分けた3個を1辺とする正三角形6つと中心の1個の合計だとわかります。
　以上のことを考えて問題を解いていくと、一番外側の1辺は 60÷6＝10、10＋1＝11(個)と求まります。また、全部の個数は 1＋(1＋10)×10÷2×6＝331(個)と求まります。
　正三角形の部分の碁石の個数を求めるのに等差数列の和を求める公式を使っています。等差数列の公式は「規則性」や「数の性質」の単元でこれからも必要になります。公式や公式の使い方がわからない場合は予習シリーズ4年上第16回を復習しまして必ず身につけましょう。　

【第1位　分配算：差が変わらない問題の線分図のかき方が理解できていますか？】

　次の問題を考えてみましょう。

　線分図に条件をまとめます。このとき、「同じものがあるときは線分図の左側にそろえる」ということを意識するとまとめやすいです。

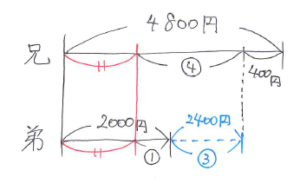
　弟の出した金額をマル1とすると兄の出した金額はマル4＋400 になります。これを線分図にかきこんでみると、マル3＝(4800－2000)－400＝2400、マル1＝800(円)となります。したがって、兄が出した金額は800×4＋400＝3600(円)とわかり、サッカーボールの値段は 3600＋800＝4400(円)と求まります。
　求めるものを間違えないように最後まで気をつけて解きましょう。

【番外編　第1回から第4回の復習：投票の問題の解き方を覚えられていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　・第1回　約数・公約数、素数
　・第2回　倍数・公倍数
　・第3回　図や表へのまとめ方、投票の問題
　・第4回　円と正多角形

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。