メールマガジン宝箱 Mail magazine

　今回のマンスリーは平面図形の相似や、変化のグラフなど、これまで習ってきた解法を限られた時間内で正しく組合せて解くタイプの難問が数多くテスト範囲に含まれます。そこで、解法を速く正確に使いこなし着実に点を取るための対策ポイントを第5位から第1位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！さらに、このランキングを実践的に身につけられるように予想問題を作っていますので、予想問題も併せてご活用ください！ショートバージョンは、こちらから無料でダウンロード頂けます！

【第5位　場合の数（投票算）：仮の競争相手を立てる式の意味を確実に理解できていますか？】

　場合の数の中に含まれる投票算は、解き方を正確に身につけておけば確実に得点源にできますが、少しでも理解が曖昧なままでは思わぬミスをしてしまう、要注意の単元です。式のかたちが単純なだけに、理解が足りないと式の立て方自体を間違えてしまいます。具体的な例をもとに式の立て方を確認しておきましょう。
　「ある中学校の生徒700人が1票ずつ投票して4人の委員を選ぶ選挙をします。投票は1人の名前だけを書き，無効票はないものとします。何票以上投票されればその人の当選が確実になりますか。ただし，立候補者は5人以上はいるものとします。」という基本パターンで考えてみます。先に正しい式を示すと、「700÷5＝140、140＋1＝141」の式より、正解は141票となります。ここで700を4ではなく5で割ることがポイントになります。
　この問題では投票数の上から4位に入れば当選します。ここで700÷4＝175（票）と考えてしまいがちですが、これは当選する4人以外全員の得票数が0票であることを前提としており、「4位になるための最多の得票数」を表します。問題では当選するための最も少ない得票数を求めますので、4位になるためには5位の生徒より1票でも多く獲得すればよいことになります。つまり「5位の生徒」という仮の競争相手を想定して解くという方針になるのです。5位の生徒が得票できる最多の数が、700÷5＝140（票）ですので、4位になるための得票数は、それに1票を足した140＋1＝141（票）となります。

　「当選する人数に1を足した数で割って、1をたす」というかたちを暗記する前に、なぜその式になるのかを必ず確認しておきましょう。それによって暗記がより確実になるだけでなく、問題の出され方が変わっても対応できるようになります。決して難しい問題ではないだけに、確実に得点しておきたいのが投票算です。曖昧な理解になっていないか、式の立て方を再度確認しておきましょう。

【第4位　平面図形（平行線と相似）：台形の面積比をできるだけ短い時間で解き進められていますか？】

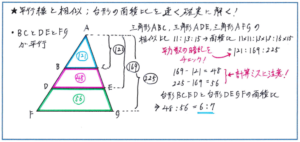
　今回のマンスリーでは平面図形の相似の問題での得点が、偏差値アップのための大きなポイントになります。その中でも三角形の中に底辺に平行な線がかかれた「ピラミッド型」の相似の図形に含まれる、台形の面積比を求める問題は、可能な限りスピーディーに、かつ正確に解答することが求められます。
　相似の図形の中でもピラミッド型のかたちは基本形で、見慣れた図形かと思われます。そこで気をつけるべきは、焦って解き進めようとして起こしてしまいがちなミスを徹底的に防ぐことです。三角形の相似比がわかった時点で、面積比をその平方数から求めるまでは基本中の基本です。この時点での解き方が曖昧な場合は、急ぎデイリーで復習を重ねてください。起こりやすいミスはその後の計算を雑に進めてしまうことにより発生してしまいがちです。
　三角形の相似比が3：2であれば面積比は9：4、よって小さな三角形と台形の面積比は4：(9－4)＝4：5といった単純な計算であれば暗算でもミスは起こらないでしょう。この相似比が13：17のような少し複雑になった場合、また三角形内にかかれた平行線が1本ではなく2本以上かかれた際に、分けられた台形の面積比を暗算で求めようとして計算ミスをしてしまうことがあるのです。
　ミス防止の対策としては、まずは面積比として求めた数字を図形内にしっかり書き込むこと。式だけで進めるのではなく視覚的にも面積比をおさえておくことが、細かなミスの防止につながります。また平方数をできるだけ暗記しておくことも対策となるでしょう。6年生のこの時期ですから15×15までは覚えられているかと思われますが、その暗記が曖昧であればマンスリーまでにしっかり固めておいてください。そのうえでできれば16×16から19×19までの計算結果も可能な限り覚えておくと時間的にも速く解き進められる効果が望めます。

　このタイプの問題はマンスリーでは図形の小問集合で出題されるか、大問の(1)として出される可能性が高いと考えられます。つまりは確実に、しかもできるだけ時間をかけずに得点をしておきたい問題となります。苦手意識もあってミスをしてしまう場合は改めて基礎固めを重ね、特に苦手意識もなく普段の演習でも間違いが少ない場合は、制限時間を設定して練習するなどして、「急いでも正解できる」まで仕上げておくとようにしましょう。

【第3位　規則性（図形の規則性）：規則性を整理するための書き出しは正確に行えていますか？】

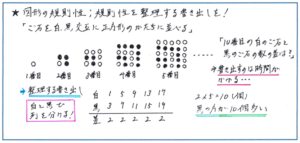
　規則性の問題の中で図形の規則性を求める問題では、与えられた図形以外に自分で内容を整理するための書き出しをすると得点のチャンスが大きく広がります。例えば下の図のような、ご石を正方形のかたちに並べるタイプの問題では、段ごとに並ぶ数の規則性自体は把握しやすく、□番目までご石を並べたときに、白のご石と黒のご石は合わせて何個あるか、といった問題であれば、□×□（個）といった答えがスムーズに求められます。それに対して「○番目に並べた白のご石と黒のご石の個数の合計の差は何個あるか」といった問題になると、解き方によっては想定外のミスを起こしてしまいます。
　そこで図だけで問題を処理するのではなく、それぞれの段にあるご石の数を表のようなかたちで書き出すと、ご石の差の規則性が一目のうちにつかみとれます。これをひたすらに図形をかき増やすなどの解法をとってしまうと、時間がかかるだけでなく計算間違いが起こる可能性も跳ね上がってしまいます。

　規則性の問題はどこまで書き出し、どこまでを計算で処理するかを迷ってしまいがちです。テストでは速く正確に解き進めることが求められますので、書き出しに使える時間には限りがあります。すべてを調べるのではなく、規則性を正しく見つけるための書き出しを行うという目的から逸脱しないよう、必要最低限の書き出しで解き進められるように、練習を重ねておきましょう。

【第2位　平面図形（四角形と面積比）：砂時計→底辺比の「視点の切り替え」はできていますか？】

　今回のマンスリーでは、平面図形の相似の単元から難度の高い問題が出される可能性が高くあります。特に平行四辺形や台形といった平行な辺を含む四角形の中に何本かの線が書き込まれたかたちから、相似の関係を見つけ出して、面積や長さを求める問題は、解法によっては必要以上に多くの時間を費やしてしまうことになります。難度の高い問題でも着実に得点をかせぐために、図形のどこに注目すればよいのかという「相似を見つける目」をしっかりと養っておく必要があります。
　相似の中でも基本の形である「砂時計型」と「ピラミッド型」の関係はしっかりと踏まえたうえで、さらにその関係から求められた比が、別のかたちで活用できないか、といった「視点の切り替え」ができるようになると、正解できる問題の幅が一気に広がります。
　例えば下の図であれば、台形ABCDの辺ADと辺BCが平行であることから、三角形ADEと三角形CBEが相似になります。ここで辺ADと辺CBの長さの比、つまり2つの三角形の相似比が3：5であるとすれば、対応する辺である辺DEと辺BEの長さの比も3：5になります。ここから「高さが共通の三角形の面積比は底辺の長さの比」という面積比の基本に立ち返ると、三角形ADEと三角形ABEの面積比がDE:BE＝3：5と求められるのです。この相似から面積比への切り替えをとにかく速く行うという意識づけが、サピックス6年のマンスリーでは必須になるのです。

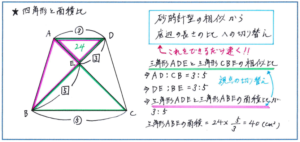
　今回ご紹介した基本レベルの問題ではなく、より複雑に図形が組み合わさっている問題でも、視点の切り替えを意識して図形を見れば、解法の糸口が見つけやすくなります。普段の演習でも正解したかどうかだけではなく、図形のどの部分に注目すればよかったのか、そのプロセスを必ず見直すようにしましょう。その積み重ねが「相似を見つける目」の養成につながります。

【第1位　変化のグラフ：比を使った断面図の利用法は身につけられたいますか？】

　グラフを用いた問題の中でも、容器に水を入れた時間と水の深さの関係を表すグラフを読み解く問題は、グラフの元になる立体図形の成り立ちを正確に見抜く力を求められる点で、難度が大きく上がるケースが多いです。もともと立体図形の問題は平面図形と比べてイメージが構築しづらいうえに、グラフを組み合わせた問題になると「変化の様子」まで細かく把握しなければならなくなるため、対応が難しくなるのです。この変化をいかにわかりやすくとらえるかが、水深変化とグラフの問題での正答率アップにつながります。
　具体的な対策として、容器の断面図を利用する方法があります。立体図形の問題では、容器に水を入れる問題以外にも、おもりを沈めるような問題でも断面図を利用するケースは多く、これまでの演習で断面図をかくこと自体は十分な経験を積んで来られたでしょう。そこでさらにグラフとの関係までしっかり踏まえられるようになると、断面図を利用する効果が一気に増します。
　例えば下の図のような階段のように直方体を組み合わせた立体が入った容器があり、それぞれの部分に水が入る時間と水の深さを表したグラフが示されているとします。大前提として、水が入る時間の比とそれぞれの部分の体積の比は等しくなります。ここで断面図を利用すれば、各部分の奥行きはすべて同じですので、体積の比は面積の比と同じくなることから、「水が入る時間の比＝面積の比」となります。さらに断面図では横の長さは底面積を表しますので、「体積比＝底面積の比×高さの比」であることから、実際の長さや面積がわかっていなくても、比を利用することで体積の比、つまりは水が入る時間の比を求めることができるのです。

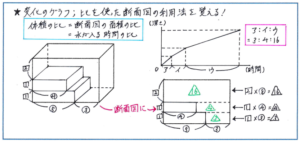
　変化とグラフの問題では、変化の様子をどれだけ正確にイメージできるかがポイントになりますので、断面図をかいたり、グラフに書き込みをするなど、イメージを視覚的に持てるような作業を積極的に進める必要があります。制限時間のあるテストで作業を効果的に進めるには、どうしても慣れが不可欠ですので、普段の演習から手を動かして作業を進める意識を持つようにしましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。