メールマガジン宝箱 Mail magazine

　新6年生になって最初のマンスリーテストです。今回のマンスリーは、テスト範囲が幅広いだけでなく、「比と割合」「速さ」「平面図形」などの重要単元について、5年終了時までに習得した知識の理解を確かめる問題が数多く出されます。さらに「N進法」や「ニュートン算」といった独特な解法を求める単元も含まれるため、知識を正確に整理し、問題内容に合わせた解法を使いこなせているかの確認が必須となります。そこで2月度マンスリーテストの対策ポイントを第1位から第5位までランキングにしましたので、ぜひマスターしてテストに臨んでださい！応援しています！
　さらにこちらの算数予想問題と組み合わせれば、マンスリーテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　速さの問題：逆比、つるかめ算の考え方を柔軟に当てはめることができていますか？】

　速さの問題では、様々な考え方を速さに当てはめて解く方法を正しく理解できているかどうかがポイントになります。速さの公式を使って解く基本問題、通過算や流水算、時計算の基本的な考え方で解く問題からは何段もレベルアップした問題が出される可能性が高くありますので、単に解き方を暗記するのではなく、速さに当てはめる考え方の、基本的な成り立ちをしっかり理解して臨む必要があります。
　例えば「平均の速さ」で、行きの速さと帰りの速さを足して2で割ってはいけないのは、平均の基本的な考え方が「全体÷個数」にあることで、個数を速さにおける「時間」に当てはめると、「(全体の距離)÷(全体の時間)」という式になるためです。
　また、途中で速さが変わる問題では「つるかめ算」の考え方を使いますが、「つるかめ算」の基本的な成り立ちは、異なる2つの要素について、その個数の合計と、1個あたりの単位量がわかっていることにあります。速さが変わるということは、全体の距離は変わらないままに、2種類の速さが発生するためで、ここで「つるかめ算」の考え方を使うことができるのです。速さの問題で平均やつるかめ算の考え方を正しく使うためには、それらの考え方の基本的な成り立ちをしっかり踏まえておくようにしましょう。

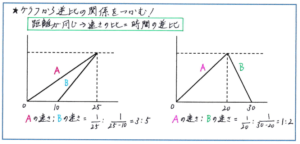
　そして、特に注意して頂きたいのが、「逆比」の考え方です。積が一定である2つの要素の間には逆比の考え方が成り立つという点は、この後の【第2位】で取り上げる面積図でも使われます。「速さ」「時間」「距離」の3つの要素について、「距離が同じならば、速さの比＝時間の逆比」の関係を使って解くタイプの問題は、今回のマンスリーはもちろん、今後のテストでも大変多く出されます。問題文の中で、「距離が同じ」と提示されている場合だけでなく、上のような、グラフの中から逆比の関係を正確につかめるように、グラフの見方もしっかり鍛えておきましょう。

【第2位　比と割合：「濃度」の問題で面積図を正確に使いこなせていますか？】

　「比と割合」の単元の中でも、今回のマンスリーでは「食塩水の濃度」からの難度の高い問題が要注意です。「食塩水の重さ」「食塩水の濃度」「食塩の重さ」の関係を把握しておくことは大前提で、単純な混ぜ合わせの問題だけでなく、「食塩水のやりとり」などの応用問題が多く出される傾向にありますので、難度の高い問題の対策までしっかり固めておきましょう。
　基本となるのは、面積図を正しく利用することです。まずは「8%の食塩水300gと濃度のわからない食塩水200gを混ぜ合わせたところ、12%の食塩水になりました。200gの食塩水の濃度は何%ですか」といった混ぜ合わせの基本パターンですぐに面積図がかけるかどうかをチェックしておきましょう。
　そのうえで気をつけて頂きたいのが、食塩水の重さが与えられていない、発展型の問題です。例えば「4%の食塩水Aと10%の食塩水Bがあり、Aの1/3とBの1/4を混ぜ合わせたら、6%の食塩水ができました。はじめの食塩水Aと食塩水Bの重さの比はいくつですか」といった問題。複雑に見える問題ですが、混ぜ合わせる2種類の食塩水の濃度と、混ぜ合わせてできた食塩水の濃度さえわかっていれば、2種類の食塩水を混ぜ合わせた重さの比（2：1）までは、面積図を使ってすぐに求められます。あとは比の計算（2÷1/3：1÷1/4＝3：2）で正解まで行き着くことができます。こうした実際の量が与えられていなくても量の比を求められる点が、面積図を使うことの大きなメリットとなります。

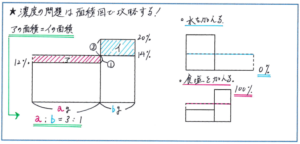
　使うメリットの大きい面積図ですが、いつでも効果を発揮するとは限りません。食塩水や食塩の量が多くわかっている場合などは、面積図を使わなくても正解に行き着くことができます。常に面積図を使わなくてはいけないといった考えにこだわらずに、問題内容に合わせて柔軟に対応できるように、面積図のかき方をしっかりマスターして、どのような場面で使うと効果があるのかを体感しておきましょう。
　また、水を加えるのであれば「0%の食塩水」と混ぜ合わせる、食塩を加えるのであれば「100%の食塩水」と混ぜ合わせるといったかたちで、どちらも面積図で解き進めることができますので、ぜひ実践してみてください。

【第3位　ニュートン算：線分図を速く正確にかいて解き進める流れは身についていますか？】

　ニュートン算は他の単元と比べて、出題のされ方がパターン化されていますので、基本的な解法をしっかり習得できていれば問題を見てすぐに解答方針が立てられます。一方で解法の覚え込みが足りないと、手も足もでなくなってしまう単元でもあります。問題のどの部分に目を着けて、どのように解き進めればよいのか、デイリーの解説も熟読して復習を進めましょう。
　ポイントになるのは、線分図を使って、いかに問題内容を正確に把握するかです。速く正確に線分図がかけるかどうかが得点の分かれ目になります。例えば、「ある水族館の入館口では、開館前に行列ができていて、その後も毎分一定の割合で来館客が行列に加わるものとします。受付窓口を9か所開けると35分で、15か所開けると14分で行列はなくなります。受付窓口を25か所開けると、何分で行列はなくなりますか。」という問題では、どのように線分図をかけばよいでしょう。

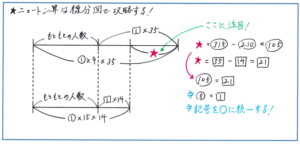
　線分図をかく流れについて念のため確認しておきましょう。
　まず、上のように2本の線分図をかき、左端にもともとあった量、この問題では「開館前に行列にいた人数」を置きます。次に単位量あたりに減る人数をマル1、増える人数をシカク1とします。ポイントはここから、線分図の差に着目してマル1とシカク1の関係を式にして、どちらかの記号に統一することです。
　この流れで進めると、まず窓口を9か所開けた場合は、35分で入館する人数がマル315、15か所開けた場合は、14分で入館する人数がマル210となります。線分図の長さの差を、マルとシカクで表すことで、マル315－マル210＝シカク35－シカク14より、マル105＝シカク21からマル5＝シカク1となります。
　そして記号をマルで統一すると、開館前に行列にいた人数がマル315－マル5×35＝マル140と表せることになります。最後に、25か所で1分間に入館できる人数がマル25、1分間に増える人数がマル5となることから、140÷(25－5)＝7より7分と答えが求められます。
　問題内容が、今回ご紹介したような行列のケースであったり、ポンプで水そうを空にするケースであったりと変わってきますが、基本的な図の成り立ちは変わりません。解き方の流れさえ確実に身につければ、テストで得点源にできる単元ですので、問題の内容がわかりづらいと決めつけずにじっくり解き進められるように、解法を身につけてください。
　ニュートン算では線分図をかくことが問題を解き進めるうえで重要にはなりますが、いつでも線分図が必要、ということではありません。もともとあった量（上の問題であれば、開館前に行列にいた人数）がわかっているタイプの問題であれば、図をかかなくとも式だけでスムーズに正解まで行き着くことができるケースがあります。問題内容によって、より短時間で、正確に正解に行き着く方法を身につけておきましょう。

【第4位　平面図形：1つの図形に相似の関係が複数あるパターンにも対応できていますか？】

　平面図形の問題では、これまでに相似・面積比を学習してきましたので、比を使った難度の高い問題が出される可能性が高くあります。相似であれば、1組のピラミッド型の相似を使うような単純なパターンではなく、1つの図形の中に複数の相似の関係が含まれるような応用問題を解き進める力まで求められると考えておきましょう。
　例えば下のような正方形の中に2つのピラミッド型の相似が含まれるパターンで、五角形CFGHEの面積が正方形ABCDの面積の何倍かを求める問題。BE：CE＝1：1、CF：DF＝1：2であり、正方形であることから、BC＝CDとなることを利用して、BE:CE＝3：3、CF：DF＝2：4と、比の和がそろうように数値を調整することがポイントになります。さらに、三角形BEH、三角形DFHの高さも比の数値で表すことができ、正方形ABCD、三角形BCD、三角形BEH、三角形DFGをすべて比の数値で表すことができれば、正解までスムーズに解き進めることができます。

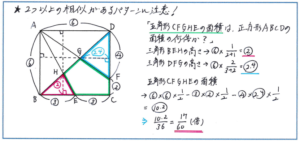
　今回ご紹介した問題は、正方形という四角形の中でも同じ長さ、同じ角度の多い特殊パターンではありありますが、図形の中から相似の関係を見つけ出して、比を使って面積を表すという流れは、多くの問題で使う鉄則のパターンです。まずは図形の中から相似の関係を的確に見つける目を鍛えて、さらには「比どうしのかけ算やわり算」を含めた比の計算を正確に進められるように、比の基本をしっかり見直しておいてください。

【第5位　場合の数：不定方程式の問題で表を活用した解き方を習得できていますか？】

　サピックスでは場合の数に属しますが、不定方程式は「つるかめ算の応用型」として扱われることもあります。2つの要素につき、単位量と合計の個数がわかっていれば「つるかめ算」ですが、そこで合計の個数が与えられていないパターンが、「不定方程式」になります。例えば、「1本60円のえんぴつと1本90円のボールペンを合わせて11本買ったところ、代金は750円になりました。えんぴつを何本買いましたか」といった問題であれば、瞬時に「つるかめ算」とわかり、えんぴつの本数を、(90×11－750)÷(90－60)＝8（本）と求めることができるでしょう。それが、「1本60円のえんぴつと1本90円のボールペンを何本か買ったところ、代金は750円になりました。えんぴつを何本買いましたか。考えられる本数をすべて答えなさい」と条件が不足すると、不定方程式になります。合計本数がわかっていないこと、そして、「考えられる本数をすべて答えなさい」といった問われ方が「つるかめ算」との大きな違いですが、特に「すべて答えなさい」は算数に限らず全教科のテストにおいて、多くのお子様方が苦手とされているパターンです。そして、この当てはまるケースをすべて答えるという点で、不定方程式は場合の数の単元とも言えるのです。
　答えが1つに定まらないことで、問題の難度が大きく上がるように思われるかもしれませんが、不定方程式は解法さえ覚え込めば、決して難しい問題ではありません。ポイントは、当てはまるケースを逃さないように、表を活用することです。
　ご紹介した問題であれば、えんぴつの本数をa本、ボールペンの本数をb本として、60×a＋90×b＝810から式全体を30で割って、2×a＋3×b＝25として、aに当てはまる数を0、1、2、…と小さい数から探していくと、a＝2、b＝7という組み合わせにたどりつきます。ここからが表の出番です。

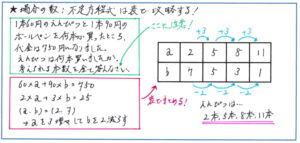
　2と3の最小公倍数が6であることから、2×aを6増やす代わりに、3×bを6減らせば、当てはまる組み合わせを順番に求めることができます。そこで、aを(6÷2＝)3増やし、bを(6÷3＝)2減らすという作業をくり返せばよいことになります。そこで、a、bに当てはまる数を表に順にうめることで、aとした「えんぴつの本数」を、2本、5本、8本、11本と求められます。
　すべて答えなさいと問われると、果てしない作業をイメージしてしまうかもしれませんが、不定方程式では、「一方を3増やして、2減らす」などのルールにそって進めればよいので、当てはまるケースはかなり限定されます。さらに表を使えば、選びもれを防ぐことができます。問題内容を式で表して、表でまとめる、といった流れをぜひとも身につけてください。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。