メールマガジン宝箱 Mail magazine

　6年生最初の組分けとなる第1回組分けテストです。新6年のカリキュラムに慣れるための大事な時期でもありますが、「規則性」「平面図形」「水量の変化」など、書き出しや書き込みなど自分の手を動かして解き進める力が求められる重要単元が多く範囲に含まれ、さらに「和と差の文章題」という図や表の活用が必須の単元も出題対象となります。

　自分の手を使ってどれだけ問題内容を整理できるかが得点の分かれ目となる第1回組分けで、クラスアップを実現して、一気に弾みをつけたいところです。

　そこで、第1回組分けテストの対策ポイントを第1位から第5位までランキングにしましたのでぜひマスターしてテストに臨んでださい！応援しています！

　さらにこちらの「50分で偏差値を5上げる算数予想問題」と組み合わせれば、組分けテスト対策は鬼に金棒です。ぜひクラスアップを実現してください。応援しています！

【第1位　平面図形：面積を求める際に、「同じ部分への移動」がスムーズにできていますか？】

　今回の組分けテストの範囲のひとつ「平面図形(1)」では、円とおうぎ形や、等積移動などの面積の求め方の工夫がメインの単元となります。5年の後期に演習した相似や面積比については、次回組分けの範囲となる、第7回の平面図形(2)で徹底的に演習するため、今回演習する範囲とは合致しませんが、この後の【第3位】で解説する「反射」では相似の考え方は利用しますし、小問集合で相似・面積比が出題される可能性もありますので、平面図形と比の基本的な理解は見直しておくようにしましょう。

　面積の問題では、円やおうぎ形と他の図形との複合図形の面積の求め方や、面積が同じ部分に着目して解く「等積移動」の考え方がしっかり理解できているかを確かめる問題が出される可能性が高いです。

　その中でも特に注意しておきたいのが、円やおうぎ形と正方形が組み合わさった図形での、正方形の面積の求め方です。正方形はひし形の一部なので、ひし形の面積の公式［対角線の長さ×対角線の長さ÷2］で求められます。この求め方を使う問題が、今回の組分けテストで出される可能性が高くありますので、1辺の長さがわかっていないからといって、面積が求められないと判断することがないようにしましょう。

　例えば、下のような「対角線の長さが12cmの正方形の中におうぎ形が含まれる図形」での斜線部分の面積の求め方をスムーズに思いつくことができているでしょうか。

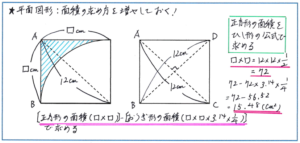
　今回ご紹介したような基本型の複合図形の問題は、テストの前半で出される可能性が高く、それだけに正解することはもちろん、できるだけスピーディーに解き進めたいところです。逆に、こうした問題で迅速に正解が得られれば、弾みがついてその後の中盤以降の問題にかける時間を短縮でき、得点を多く重ねるチャンスが一気に広がります。面積や角度の基本的な解法を確実に覚えられているか、しっかりチェックしておきましょう。

【第2位　水量・水深の変化：容器を断面で見て考える解法を使いこなせてていますか？】

　水量・水深の変化の問題の得点力を上げられるかどうかは、断面図をかいて解き進められるかどうかで決まります。複雑な問題になればなるほど、問題内容を断面図で整理して、そこから比を使った解法を使いこなす力が求められます。まずは簡単な問題で図に状況をまとめる練習をして、応用問題でも図がかけるような力を養成しましょう。

　例えば、「下の（図1）のような水そうに10cmの深さまで水が入っています。（図2）のような棒が何本かあり、この棒を底面が水そうの底にぴったりとつくように入れていきます。棒を何本か入れると、水の深さが18cmになりました。何本の棒を入れましたか。」といった問題で、断面図を正確に利用できるでしょうか。

　断面図では、縦の長さを「高さ(深さ)」に、横の長さを「底面積」とします。与えられた数値として、水そうの底面積が、20×18＝360（平方cm）、もとの水の深さが10cm、増えてできた水の深さが18cmを、（図3）の断面図にかき込みます。

　そこで斜線部分の面積が等しくなることから、斜線の長方形の横の長さの比は、たての長さの比の逆比となります。たての長さの比が、10：(18－10)＝5：4のため、横の長さの比が、1/5：1/4＝4：5となり、棒を入れる部分の底面積が、360×4/9＝160（平方cm）となるため、底面積の計算から、入れる棒の本数が、160÷(5×4)＝8（本）と求められます。

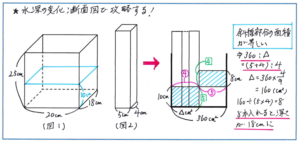
　このように基本的な問題で断面図のかき方を練習していけば、今回ご紹介したような、おもりを複数沈める問題だけでなく、おもりを引き上げたりする問題、さらには仕切りや腰かけが入った水そうに水を入れるタイプの問題でも、幅広く対応できる力が大きくアップします。繰り返し練習して確実に身につけていきましょう。

【第3位　反射の問題：線対称の作図で、頂点を正しくかき入れられていますか？】

　予習シリーズ第3回の新出テーマ「反射の問題」は、平面図形の「相似」の考え方を使いこなす力が求められる重要単元で、今回の組分けテスで出題される可能性がとても高いです。線対称の考え方を使った作図方法をマスターできていれば十分に得点源とできる単元なですが、その解法が定着していないと、どこから手をつけてよいのかに迷い、その結果、得点に至ることができないといった状況が起こりがちな要注意単元です。練習の段階では時間がかかっても、線対称を使った作図方法を確実に身につけておきましょう。

　例えば、下の（図1）で「点Aを発射した光が辺上を2回反射して点Cに着くとき、DEの長さは何cmか」といった問題であれば、長方形ABCDについて辺CDを軸に線対称な長方形をかくのですが、この問題のように「2回反射」の場合は、新たな長方形を2つと、反射の回数と同じ数だけかいて、頂点Aと到達点C（折り返し点）を直線で結ぶことで準備は完了です。

　ここで三角形ADEと三角形Xが相似であることを利用して、DE＝15×1/3＝5（cm）と求めることができます。

　同じ考え方を使って、下の（図2）で「点Bを発射した光が辺上を4回反射して点Dに着くとき、CFの長さは何cmか」といった問題であれば、長方形ABCDについて辺BCを軸に線対称な長方形を4つかき、頂点Bと到達点D（折り返し点）を直線で結びます。

　そして三角形BCFと三角形Yが相似であることを利用して、CF＝15×1/5＝3（cm）と求めることができます。

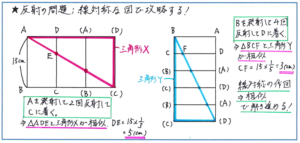
　反射の問題の中には線対称の考え方を使わなくても解答できる問題があります。線対称の作図には手間と時間がかかることは避けられませんので、問題をよく読んで、線対称の作図が必要かどうかの判断をスピーディーにできるようにしておいてください。それでも、線対称の考え方を使いこなすことができれば、どのような問題にも対応することができますので、テスト会場で極力時間をかけずにスムーズに作図ができるように、線対称の図形を正確にかく練習を重ねておきましょう。

【第4位　いもづる算：式を立てて表で一気に解決する流れをマスターできていますか？】

　つるかめ算の応用型である「いもづる算」は、応用型とはいえ、基本的なつるかめ算からは難度が大きく跳ね上がり、一連の解法の流れをマスターしていなければ、正解のチャンスが大きく遠のいてしまいます。ここでは基本的な問題を題材として、解法を確かめておきましょう。

　例えば、「1個90円のキャラメルと1個50円のチョコレートをいくつか買って、代金の合計を1330円にするとき、キャラメルとチョコレートをそれぞれ何個買えばよいですか。あてはまる組み合わせをすべて求めなさい。」といった問題で考えてみます。

　まず式の立て方ですが、キャラメルの個数を○個、チョコレートの個数を□個とすると、90×○＋50×□＝1330という式になります。最初のポイントは「式を簡単にすること」にあります。これは単純に計算をしやすくするためです。ここでは式の両辺を10で割って、9×○＋5×□＝133となります。

　ここからはあてはまるケースをひとつ導き出すのですが、どちらかの個数をできるだけ多くして調べるという方法にすぐに着手するのではなく、式をよく見て何か工夫ができないか、考えてみましょう。注目すべきは「5×□」の1の位の数が必ず0か5になるため、9×○の1の位を3か8になるということです。そこで○を小さい数から調べてみると、9×2＝18があてはまります。

　このとき○＝2で、□＝(133－9×2)÷5＝23より、（○、□）＝（2、23）の組み合わせが導き出せます。ここからは、「○を5増やし、□を9減らしても合計金額は変わらない」という鉄則にそって、下のような表を作れば、正解が（2、23）、（7、14）、（12、5）と求めることができます。

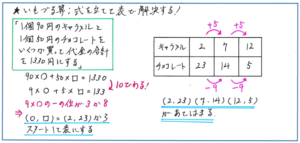
　いもづる算の中にも予習シリーズで紹介されているような、様々なタイプの応用問題がありますが、3まずは基本タイプで解法の流れを着実に進められているかどうか、しっかりチェックしておきましょう。いもづる算に限らず、条件が少ない問題は受験生にとって解きづらさを強く感じさせるものです。それだけに、解法の流れを習得して実践できているかどうかが大きな得点の分かれ目になりますので、いま一度、理解を確かめておいてください。

【第5位　日付の問題：どこを起点に日数を数えるかで迷うことはありませんか？】

　数と規則性の中でも「日付」に関する問題は、苦手とするお子様がとても多い単元です。問題の種類は限られており、問題文自体は複雑ではないのですが、月によって30日か31日か（あるいは28日か29日か）という場合分けが必要になること、そして、日数を計算する際に「その日を含むかどうか」といった、数え始める起点まで考えなくてはいけないことといった、処理しなければならない情報が想定よりも多い点が、問題を難しく感じさせています。

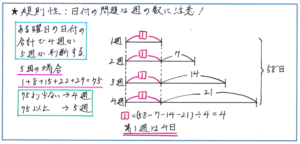
　例えば次のような問題には、どのように対応すればよいでしょうか。「ある年の8月の火曜日の日付の合計は58でした。この年の8月の第3火曜日は8月何日ですか。」

　ここでは、この年の8月の火曜日が4週あるか、5週あるかの確認が必要になります。ここは『予習シリーズ算数6年上』の25ページに掲載された解説の通り、火曜日が4週ある場合と5週ある場合の違いをしっかりおさえておく必要があります。

　もしも火曜日が5週あるとすると、火曜日の日付の合計が最小でも1＋8＋15＋22＋29＝75となることから、8月の日付の合計が58であるため、火曜日は「4週」と定められます。この流れは、日付に関する問題を解く上で必須になりますので、しっかり習得しておきましょう。

　あとは線分図を利用して、第1火曜日をシカク1として、シカク1＋（シカク1＋7）＋（シカク1＋14）＋（シカク1＋21）＝58より、シカク4＝58－42、シカク1＝4となり、8月の第1火曜日が8月4日となり、第3火曜日が、4＋14＝18より、8月18日と求められます。

　こうした「場合分け」を使う問題は、これから「規則性」や「場合の数」に限らず、多くの単元で使うことになります。問題内容を理解したうえで、どの部分での「場合分け」が必要になるか、といった高いレベルの判断が求められるのが6年生の算数ならでは、と言えます。逆に「場合分け」を正しく使いこなせれば、難問への対応力が一気にアップしますので、解法を地道に身につけていきましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。