メールマガジン宝箱 Mail magazine

　5年生は「点の移動」「図形の回転移動」「円の転がり運動」といった図形の移動に関する問題、さらには「年令算」「いもづる算」といった、難問が出題されやすい単元がテスト範囲になります。特に図形の移動の問題では、自分で図をかいて解法を見つけ出すことが攻略のポイントになります！図をかいて移動の様子を正確にイメージできれば、一見難しい問題での得点力が飛躍的にアップします。図をかく作業を重ねることで、新6年生になってからの図形問題への対応力に断然の違いを生み出せます！

　4年生も速さや場合の数など、難度のアップした単元が範囲となります。特に速さは問題を読んですぐに式が立てられるレベルを超えた問題が出題されます。そこで線分図で状況を整理する作業が不可欠となります。この作業を今のうちから地道に取り組んでおくことで、5年生以降になって速さ、あるいは割合の難問に臨む際に、速く正確な図をかくことができるようになり、速さを得意分野にできるチャンスが大きく広がります！

　難問の出題が予想される組分けテスト！そこで今回は、ぜひ気をつけて頂きたいポイントを、5年生は第5位から第1位まで、4年生は第3位から第1位までのランキングのかたちにまとめました。ぜひクラスアップを実現してください！応援しています！
　さらに、このメルマガの5年生のランキングは明日公開の予想問題と連動しています。ランキングで紹介する攻略ポイントと予想問題を合わせれば、万全の構えで年度内最後の組分けテストに臨めます。
予想問題はこちらのページで無料公開します！

《5年　第9回組分けテスト》

【第5位　年令算：登場人物が多い問題で、正確に式が立てられていますか？】

　年令算では、「人は1年に必ず1才年をとる」という当たり前のことがとても重要です。特に2人以上で年令の和を考えるときに注意しましょう。

という問題で年令算の基本的な考え方を確認してみましょう。
　まず、求めるものをマル1年後とします。次に問題文から比例式をたてます。そして、その比例式を解いて、マル1を求めると答えになります。
　実際にやってみましょう。求めるものをマル1年後として、比例式をたてると、(74＋マル1×2)：(12＋10＋7＋マル1×3)＝2：1となります。内項の積と外項の積は等しいので、(29＋マル3)×2＝(74＋マル2)×1となり、式を展開すると58＋マル6＝74＋マル2となります。マル4＝16なので、マル1＝4となり、答えは4年後と求まります。
　このような方針で考えていくと迷うことは減っていきます。解き方のパターンとして押さえておきましょう。

【第4位　円周上の点の移動：図をかいて「角速度」を理解しましょう！】

　次の問題を考えてみましょう。

　円周上の点の移動では、角速度を使って問題を解いていきます。予習シーズ5年下第11回で学習した時計算のときの考え方と同じです。しっかりと図をかいて考えていきましょう。
　まず、角速度を求めます。Pは 60÷5＝12(秒) で1周しますから、Pの角速度は 360÷12＝30(度/秒) と求まります。同様にQは 60÷3＝20(秒)より、角速度は360÷20＝18(度/秒) と求まります。
　次に求める時間をマル1秒後とすると、角AOP(点Pが移動した方の中心角)＝30×マル1＝マル30、角AOQ(点Qが移動した方の中心角)＝18×マル1＝マル18 と計算できます。

(1) AP＝AQとなる場合
　図をかいてみると図1のようになります。

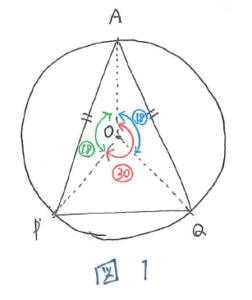
　三角形APOと三角形AQOが合同であることが分かるので、角AOP＝角AOQ＝マル18となります。すると、マル18＋マル30＝360(度)となっているので、マル48＝360、マル1＝7.5となり、7.5秒後と求まります。

(2) PA＝PQとなる場合
　 図をかいてみると図2のようになります。

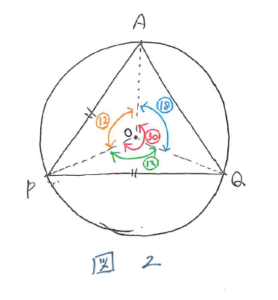
　AO＝QO（円の半径）より、三角形PAOと三角形PQOが合同であることが分かるので、角AOP＝角QOP＝マル30－マル18＝マル12となります。すると、マル12＋マル30＝360(度) となっているので、マル42＝360(度)、マル1＝8・4/7となり、8・4/7秒後と求まります。

(3) QA＝QPとなる場合
　図をかいてみると、三角形QPOと三角形QAOが合同になるはずですが、角QOP＝マル12、角QOA＝マル18 となるので、点Pが1周するまでにQA＝QPとなることはありません。

　以上より、答えは7.5秒後と求まります。

　このように角速度を使って考えていくと、円周上の点の移動に関する問題はかなり解き易くなります。入試問題などでも出題される「半径の違う円の円周上を点が移動する問題」も角速度を使えば同じように考えることができます。ぜひ身につけておきたい解法の1つです。

【第3位　円の転がり移動：円の通らない部分を忘れずに解いていますか？】

　図形の移動の問題は、図をかかないと計算が始められません。問題文に注意して図をかく練習を繰り返しましょう。

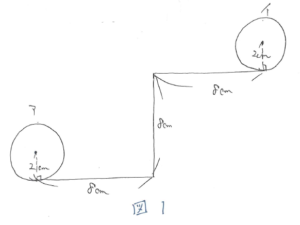
という問題を考えてみましょう。
　図をかいてみると図2のようになります。

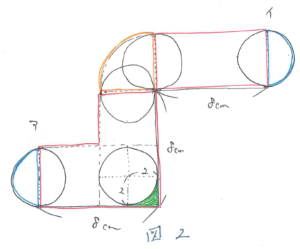
　ここで注意点が2つあります。
　1つ目は図2の緑の場所のように円が通れない部分があることです。この部分は正方形から四分円をひくことにより求められます。
　2つ目は問題文の「移動したあと」の意味です。移動したあと(後)ではなく、移動したあと(跡)のことです。つまり求める面積は、「移動前＋移動中＋移動後」となります。
　図2を見ながら方針を考えると、「赤の部分＋青の部分＋オレンジの部分－緑の部分」で面積が求められることがわかります。
　したがって、
4×8＋4×4＋4×8＋2×2×3.14＋4×4×3.14×1/4－(2×2－2×2×3.14×1/4)＝80＋(4＋4)×3.14－0.86＝104.26(平方cm)と求まります。
　計算の工夫をしたうえで、3.14の小数計算を正確にできるだけの計算力も必要になります。図をかく練習にも計算練習にもなるので、この問題以外の「円の転がり移動」の問題も積極的に練習しておきましょう。

【第2位　いもづる算：3つを2つにするポイントは平均の考え方です！】

　3量のいもづる算のポイントは、問題文の条件を上手く使って2量のつるかめ算に直して考えることです。実際に確認してみましょう。

　200円のノートをあと2冊買ったことにすると、冊数は21＋2＝23(冊)、代金は3890＋200×2＝4290(円)にかわります。このとき、200円のノートの冊数は150円のノートの冊数の4倍になっているので、「200円のノート4冊と150円のノート1冊を組にして、平均の値段を考える」ことができます。(200×4＋150×1)÷(4＋1)＝190(円)と計算でき、200円、150円という2種類の金額を190円にまとめることができました。
　条件を整理すると、はじめの問題文から、「1冊190円と180円の2種類のノートを合わせて23冊買ったところ、代金は4290円になりました。」に変化したことになります。
　つるかめ算を使って190円のノートの冊数を求めると、(4290－180×23)÷(190－180)＝15(冊)となります。よって200円のノートの冊数は、15÷(4＋1)×4＝12(冊)となりますが、ここで安心してはいけません。計算し易いように200円のノートは2冊多く買ったことにしていたので、実際の冊数は12－2＝10(冊)になります。
　今回は取り上げませんでしたが、3量のいもづる算には「全部で何通りですか」と調べなければ解けない問題もあります。手際よく調べられるように、こちらのパターンの問題も練習しておきましょう。

【第1位　図形の回転移動：移動を把握するための記号のかき入れはできていますか？】

　多角形が直線上を転がるときは、頂点が順番に直線上に来ます。この性質を上手く利用するために、頂点が全部かかれていない図形には必ず頂点をかき加えてから図をかきましょう。ミスや勘違いが格段に減ります。

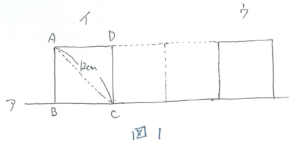
　頂点に注意して図をかきます。これに頂点Bが動いたあとの線をかき込んでいきます。1回目の回転は頂点Cを中心とする四分円になります。2回目の回転は頂点Dを中心とする四分円になり、3回目の回転は頂点Aを中心とする四分円になります。今かき込んだ線と直線アとで囲まれる部分が求める面積です。注意して図を見ると、四分円の面積だけではなく直角二等辺三角形2つ分(正方形1つ分)の面積も必要だとわかります(図2)。

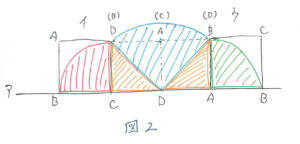
　また、頂点C、頂点Aを中心とする四分円は半径が求められないので、半径×半径を求めて面積を計算します。この半径は正方形ABCDの１辺の長さと等しいので、正方形の面積を利用して、半径(１辺)×半径(１辺)＝12×12÷2＝72となります。
以上より、72×3.14×1/4＋12×12×3.14×1/4＋72×3.14×1/4＋12×12÷2＝298.08(平方cm)と求まります。
　半径がわからなくても、半径×半径がわかれば円やおうぎ形の面積は計算できます。よく使う考え方なので合わせて復習しておきましょう。

【番外編　第11回から第14回までの復習：ニュートン算の図のかき方を覚えていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　第11回　時計算
　第12回　流水算、通過算
　第13回　仕事算、ニュートン算
　第14回　容器を傾ける問題

　また、今回の組分けテストは学年末ですが、いつもの組分けテストと同じです。全範囲ではないことに注意しましょう。

《4年　第9回組分けテスト》

【第3位　立方体と直方体：6方向から図形を見ることがポイントです！】

　4年上第14回では立方体と直方体が単独で出てきましたが、今回はそれらの応用です。組み合わせてあったり、取り除いてあったりする立体の体積、表面積を考えることが中心となります。
　典型的な問題で解き方の確認をしてみましょう。

　表面積を求めるときは「前後、上下、左右」の6つの方向から見て考えます。「前」から見ると、大きい正方形の上に小さい正方形が乗っているように見えます。「後」「左」「右」から見ても同様に見えます。「上」から見ると、大きい正方形の中に小さい正方形が含まれているように見えます。表面積の計算上はまとめて「大きい正方形１つ分」とすれば計算が楽になります。最後に「下」から見ると、大きい正方形が見えます。このことから表面積は、大きい正方形6つと小さい正方形4つの合計だとわかります。
　小さい立方体の1辺を□とすると、10×10×6＋□×□×4＝856となり、□×□＝64、□＝8と計算できます。したがって体積は、8×8×8＝512(立方cm)と求まります。
　この単元は、求めるものを間違えるミスが目立ちます。求めるものが「長さ」なのか「表面積」なのか「体積」なのかしっかり確認するようにしましょう。

【第2位　場合の数：順列と組合せを確実に区別できていますか？】

　4年下第14回で学習した並べ方(順列)と4年下第18回で学習した選び方(組み合わせ)はどちらも今回の組分けの範囲です。考え方が混ざらないように注意が必要です。
　両方の考え方を使う問題で確認してみましょう。
「0、1、2、3、4、5の6枚のカードがあります。この中から3枚のカードを取り出して3けたの整数を作るとき、3の倍数は何通り作れますか。」
　この問題で樹形図を使って3けたの整数を作り、それを3で割れるのか確かめているとものすごく時間がかかります。そこで次のように2段階に分けて考えていきます。
(1) 3つの数字の和が3の倍数になる組み合わせを調べる。
(2) (1)で調べた組み合わせのそれぞれについて、カードの並べ方が何通りあるかを調べる。
　まず(1)から考えます。和で分けて考えると調べ易いです。
　・和が3のとき、(0、1、2)…(ア)
　・和が6のとき、(0、1、5)…(イ)、
(0、2、4)…(ウ)、(1、2、3)…(エ)
　・和が9のとき、(0、4、5)…(オ)、
(1、3、5)…(カ)、(2、3、4)…(キ)
　・和が12のとき、(3、4、5)…(ク)
　次に(2)を考えます。
　(ア)は百の位に0が使えないことに注意して並べると、102、120、201、210の4通りあります。0が入っている組み合わせの(イ)、(ウ)、(オ)も同じく4通りずつあります。(エ)は、123、132、213、231、312、321の6通りあり、(カ)、(キ)、(ク)も同じく６通りずつあります。このことから、4×4＋6×4＝40(通り)と求まります。
　組み合わせを調べてそれを並べるという考え方は、場合の数の調べるときにとても有効な考え方です。練習を繰り返して確実に身につけておきましょう。

【第1位　速さ：一見複雑な問題も、線分図で整理すれば一気に解きやすくなります！】

　次の問題を考えてみましょう。

　線分図に整理しながら考えましょう。線分図に「家」「本屋」「学校」とわかっている道のりと時間を書き込みます。
　まず毎朝学校に着く時間を求めます。1800÷60＝30(分)かかることがわかったので、線分図に8:30と書き込みます。
　次に「ある日」の動きを追っていきます。本屋までは240÷60＝4(分)かかるので、線分図の下に家から本屋まで矢印をひき、本屋のところに8:04と書き込みます。ここから家に戻るのに240÷120＝2(分)かかるので、本屋から家まで2本目の矢印をひき家のところに8:06と書き込みます。忘れ物を探し終わって家から学校に行くので家から学校まで3本目の矢印をひき、学校のところに8:32と書き込みます。これはいつもより2分遅れているためです。家から学校まで走ると1800÷120＝15(分)かかるので、家を出たのは32－15＝17(分)とわかります。したがって、忘れ物を探していた時間は17－6＝11(分間)と求まります。
　今までの単元と比べると文章が長く条件も多いです。線分図に整理しながら解くと、自分の頭の中だけで考えるよりもはるかに状況が分かり易くなります。ミスの防止にも役立ちますので線分図を活用してみてください。

【番外編　第11回から第14回までの復習：樹形図を見やすくかけていますか？】

　点数にして約3割を占めます。もう一度基本事項を確認して「簡単な問題なのにやり方を忘れていて解けなかった」という事が無いようにしましょう。特に確認したいものは以下の通りです。
　第11回　分数のかけ算・わり算
　第12回　消去算(代入法)　3量の消去算
　第13回　割合の3用法
　第14回　樹形図の利用

　また、今回の組分けテストは学年末ですが、いつもの組分けテストと同じです。全範囲ではないことに注意しましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に100％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。