メールマガジン宝箱 Mail magazine

　新年度最初のテストで偏差値を大幅にアップさせ、ロケットスタートをとるためのポイントは、計算のミスを防ぐための様々な工夫をすることです！3.14でまとめて計算をする、1/4＝0.25などの分数と小数の変換を覚えておくといった計算そのものを工夫するだけでなく、面積図などの図を活用して式の数を最小限におさえるなど解法を工夫することも、計算ミスを減らす大きな効果があります。学年が変わり、単元を問わず問題の難度も上がってくるテストだからこそ、計算ミスの防止が結果として得点力の飛躍的なアップに結び付きます！いかにして計算のミスを防ぐための工夫をするかを中心にポイントを説明していきます。ぜひ、偏差値アップ、クラスアップを実現してください。応援しています！
　さらに、このメルマガは明日公開の予想問題と連動しています。これから紹介する3つのポイントと予想問題を合わせれば偏差値がかつてないレベルにまで到達します！
予想問題はこちらのページで無料公開します！

【直前チェックポイント１：3.14をまとめて計算できていますか？】

　平面図形の円や、立体図形の円柱、円すいの問題では3.14計算をいかに最小限にとどめるかが勝負の分かれ目になります。例えば下の図のような円すいの表面積を求める問題。

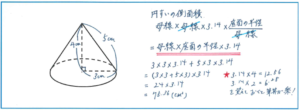
　円すいの表面積は底面積と側面積に分かれますが、側面積が「母線×底面の半径×3.14」で求められることが覚えられていない場合は、展開図を使って考えてみましょう。円すいの側面積＝母線×母線×3.14×（底面の半径／母線）の式からも上記の式を導くことができます。
上の図の円すいの表面積は、以下の式で求められます。
底面積→3×3×3.14
側面積→5×3×3.14
この2つの和を求める際に、3.14×1ケタの数を確実に覚えられていれば、
3×3×3.14＋5×3×3.14＝(9＋15)×3.14＝24×3.14＝75.36（㎠）
としたうえで、筆算では3.14×2と3.14×4が暗算で出せますので、楽に答えに行き着けるでしょう。また、3.14×3＝9.42がすぐに出てくるのであれば、
3×3×3.14＋5×3×3.14＝(3＋5)×(3×3.14)＝8×9.42＝75.36（㎠）
とすることで筆算が楽になる効果があります。
　いずれの方法にしても、まず式を3.14でまとめること、3.14×1ケタの計算結果を覚えておくことで、工夫のバリエーションが一気に広がり、計算ミスを防ぐことができます。

【直前チェックポイント２：つるかめ算の式の立て方が曖昧な場合は図を活用しましょう！】

　つるかめ算は速さなど様々な単元で使われる大事な解法です。使う頻度も高いので、式を立てる際に迷うことは少ないかと思いますが、もしも曖昧になった場合には、図を活用するとよいでしょう。
　例えば次のような速さの問題。

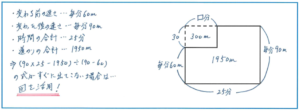
　もちろん、つるかめ算の式を確実に使いこなして、(90×25－1950)÷(90－60)＝300÷30＝10（分）とできれば、時間も短く正解に行き着くことができます。ただ、90×25と60×25のどちらを式で使えばよいか…など、少しでも迷ってしまったならば、その時間がもったいないですので、図を使ってみましょう。ミスを防止する効果が絶大です。
　図をかく際、長さについては与えられた毎分60mと毎分90mの大小関係が崩れなければ、あとは厳密にする必要はありません。多少線が曲がっても全く問題ないです。大事なのは、図に数値をかき込みながら内容を整理して、計算が楽になる過程を体感することです。
　式もひとつにすることにこだわる必要はありません。与えられた条件からわかる限りの数値をかき込んで行けば正解に行き着けます。90－60＝30より点線のたての長さが毎分30m、大きな長方形の面積が90×25＝2250（m）、そして実際に進んだ道のり1950mが太字の図形であるため、点線と実線で囲まれた小さな長方形の面積が2250－1950＝300（m）と求められれば、あとは300÷30＝10（分）と答えを求められます。時間がかかる作業に見えるかもしれませんが、うろ覚えの式で解くよりも断然正確ですし、慣れれば図をかく時間も短縮できます。いかにして確実に正解に行き着くか、そのために図を活用することも計算の工夫になるのです。

【直前チェックポイント３：仮の数を置くときは計算しやすい値にしましょう！】

　例えば食塩水の濃度で以下のような問題があります。

　混ぜ合わせの問題は面積図あるいは天びん図を活用することが必須ではありますが、上記のような問題であれば図を用いなくとも正解に行き着けます。食塩水の量がＡ、Ｂともにわかっていないので、ここで仮の数値を置いて解く方針で進めてみます。そこでポイントとなるのが、仮の数値の置き方です。%の計算がしやすく、ミスを防ぎやすくするために、食塩水Ａを100ｇ、食塩水Ｂを200ｇと100の倍数にするとよいでしょう。100×0.06＝6（食塩水Ａに含まれる食塩の量）、200×0.09＝18（食塩水Ｂに含まれる食塩の量）と計算が楽になります。あとは(6＋18)÷(100＋200)×100＝24÷3＝8（%）と進めれば、スムーズに正解が求められます。
　まずは面積図などの図の活用を第一としたうえで、図なしで解き進める方法も備えておくとテストに臨む精神的負担が軽くなります。その際には、計算を少しでも楽にすることを最優先しましょう。
　同じことは、仕事算での全体の仕事量の置き方にもあてはまります。「全体を1」としてしまうと、個人の仕事量が分数になってしまい、計算ミスが起きやすくなってしまいます。全体の仕事量は最小公倍数とすることがすぐに思いつくように、式の立て方に注意しながら練習を重ねましょう。

　われわれ中学受験鉄人会のプロ家庭教師は、常に１００％合格を胸に日々研鑽しております。ぜひ、大切なお子さんの合格の為にプロ家庭教師をご指名ください。